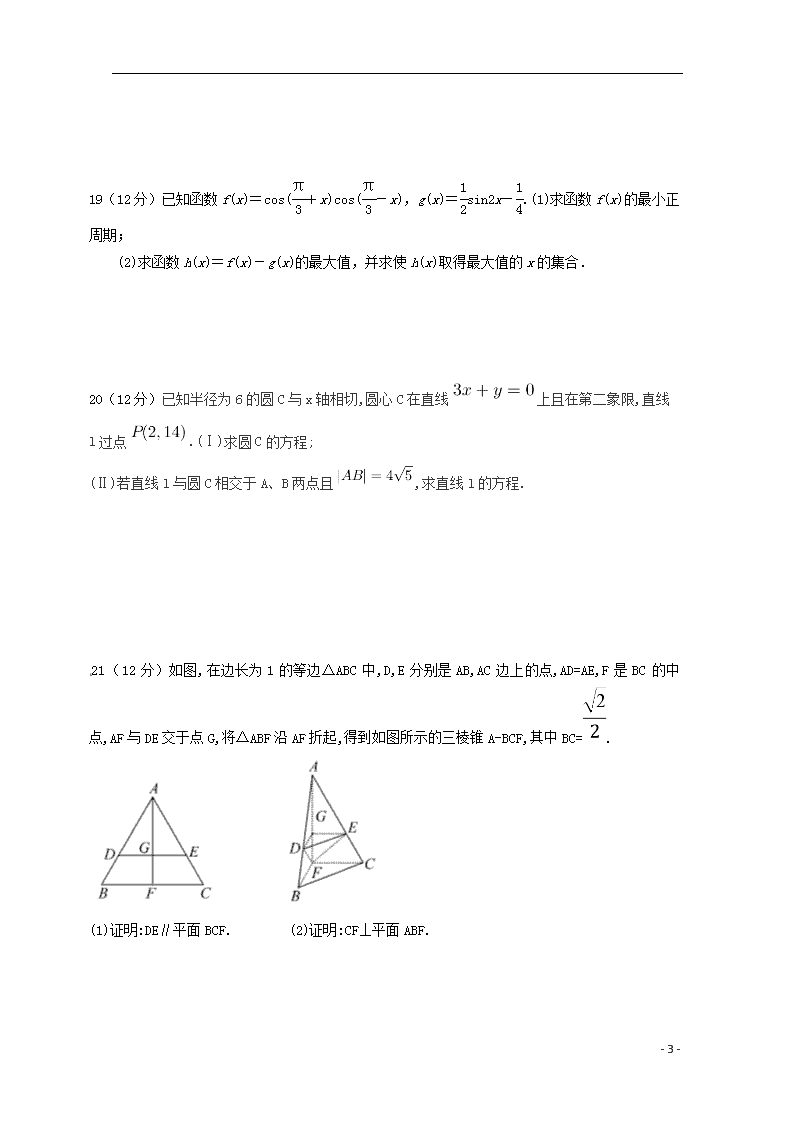2020学年高一数学下学期第二次月考试题(新版)新人教版
新疆2019学年高一数学下学期第二次月考试题
一、 选择题(12*5=60)
1、 函数y=的定义域为A,不等式>0的解集为B,则A∩B=( )
A. B. C. D.
2、函数y=+的值域是( ).A.{0,2} B.{-2,0} C.{-2,0,2} D.{-2,2}
3、已知sin=,则sin的值为( ).A. B.- C. D.-
4、以下命题:①若=,则A、B、C、D四点是平行四边形的四个顶点;②若m=n,n=k,则m=k;③若m∥n,n∥k,则m∥k;④单位向量都是共线向量.其中,正确命题的个数是( ).
A.0 B.1 C.2 D.3
5、已知函数y=Asin(ωx+φ)+m的最大值是4,最小值是0,最小正周期是,直线x=是其图象的一条对称轴,则下面各解析式符合条件的是( ).
A.y=4sin+2 B.y=2sin+2 C.y=2sin+2 D.y=2sin+2
6、若cos(α-β)=,cos 2α=,并且α、β均为锐角,且α<β,则α+β的值为( ).
A. B. C. D.
7、若2cos2α=sin(-α),且α∈(,π),则sin2α的值为( )
A.1 B.- C.- D.
8、如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( ).
A.y=sin B.y=sin C.y=sin D.y=sin
9、直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2,则k的取值范围是( )
- 11 -
A.[-,0] B.(-∞,-]∪[0,+∞) C.[-,] D.[-,0]
10、函数f(x)=sin 2x-cos 2x的图象可以由函数g(x)=4sin xcos x的图象( )得到.
A.向右移动个单位 B.向左移动个单位 C.向右移动个单位 D.向左移动个单位
11、函数g(x)=sin22x的单调递增区间是( )
A.[,+](k∈Z) B.[kπ,kπ+](k∈Z)
C.[+,+](k∈Z) D.[kπ+,kπ+](k∈Z)
12、函数f(x)=(1+cos2x)sin2x是( )
A.周期为π的奇函数 B.周期为π的偶函数 C.周期为的奇函数 D.周期为的偶函数二、填空:(4*5=20)
13、角的终边经过点且,则_____________.
14、代数式:sin2cos3tan4的符号是____________.
15、已知,,则的值为____________.
16、已知,sin()=- sin则cos= ____________.
一、 解答:
17、(10分)已知:,为锐角,求
18(12分)已知函数的部分图象如图所示. (1)求函数的解析式;
(2)将此函数的图像向右平移后,得到g(x)的图像,试求g(x)的单调区间
- 11 -
19(12分)已知函数f(x)=cos(+x)cos(-x),g(x)=sin2x-.(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
20(12分)已知半径为6的圆C与x轴相切,圆心C在直线上且在第二象限,直线l过点.(Ⅰ)求圆C的方程;
(Ⅱ)若直线l与圆C相交于A、B两点且,求直线l的方程.
21(12分)如图,在边长为1的等边△ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图所示的三棱锥A-BCF,其中BC=.
(1)证明:DE∥平面BCF. (2)证明:CF⊥平面ABF.
- 11 -
22(12分)在△ABC中,a,b,c分别是角A,B,C的对边,=(2a+c,b),=(cosB,cosC),且=0.
(1)求角B的大小.(2)设函数f(x)=sin2xcos(A+C)-cos2x,求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
- 11 -
2020届第二次月考数学试卷
出卷人:严华 审核:卿雪华
一、 选择题(12*5=60)
1、 函数y=的定义域为A,不等式>0的解集为B,则A∩B=( )
A. B. C. D.
解:由解得-1
0,得>0,所以-23.选C
2、函数y=+的值域是( ).A.{0,2} B.{-2,0} C.{-2,0,2} D.{-2,2}
解析 化简得y=+,当x的终边分别在第一、二、三、四象限时分类讨论即可.答案 C
3、已知sin=,则sin的值为( ).A. B.- C. D.-
解析 ∵sin=,∴sin=sin=sin=.答案 C
4、以下命题:①若=,则A、B、C、D四点是平行四边形的四个顶点;②若m=n,n=k,则m=k;③若m∥n,n∥k,则m∥k;④单位向量都是共线向量.其中,正确命题的个数是( ).
A.0 B.1 C.2 D.3
解析 ①A、B、C、D四点可能共线;③当n=0时,命题不成立;④单位向量的模相等,但方向不确定,所以未必共线。答案 B
5、已知函数y=Asin(ωx+φ)+m的最大值是4,最小值是0,最小正周期是,直线x=是其图象的一条对称轴,则下面各解析式符合条件的是( ).
A.y=4sin+2 B.y=2sin+2 C.y=2sin+2 D.y=2sin+2
解析 ∵最大值是4,故A不符合题意.又∵T==,∴ω=4,故排除B.
又4x+=+kπ⇒4x=+kπ⇒x=+=,所以k=∉Z,排除C,故选D.答案 D
6、若cos(α-β)=,cos 2α=,并且α、β均为锐角,且α<β,则α+β的值为( ).
- 11 -
A. B. C. D.
解析 ∵0<α<β<,∴-<α-β<0,0<2α<π,∴由cos(α-β)=,得sin (α-β)=-,由cos 2α=,得sin 2α=.∴cos(α+β)=cos=cos 2αcos(α-β)+sin 2αsin(α-β)=×+3×=-.又α+β∈(0,π),∴α+β=. 答案 C
7、若2cos2α=sin(-α),且α∈(,π),则sin2α的值为( )
A.1 B.- C.- D.
答案 C 解析 由2cos2α=sin(-α),得2(cos2α-sin2α)=(cosα-sinα).
因为α∈(,π),所以cosα-sinα≠0,所以cosα+sinα=.
又(cosα+sinα)2=1+2sinαcosα=1+sin2α=,所以sin2α=-,故选C.
8、如图所示是y=Asin(ωx+φ)(A>0,ω>0)的图象的一段,它的一个解析式为( ).
A.y=sin B.y=sin C.y=sin D.y=sin
解析 由图象可知,A=,T=-=π,∴ω==2,∴y=sin(2x+φ),将点代入,得=sin,φ-=,∴φ=,∴y=sin,故选D. 答案 D
9、直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2,则k的取值范围是( )
A.[-,0] B.(-∞,-]∪[0,+∞) C.[-,] D.[-,0]
答案 A 解析 设圆心(3,2)到直线y=kx+3的距离为d,由弦长公式得,|MN|=2≥2,故d≤1,即≤1,化简得8k(k+)≤0,∴-≤k≤0,故k的取值范围是[-,0].故选A.
10、函数f(x)=sin 2x-cos 2x的图象可以由函数g(x)=4sin xcos x的图象( )得到.
- 11 -
A.向右移动个单位 B.向左移动个单位 C.向右移动个单位 D.向左移动个单位
解析 ∵g(x)=4sin xcos x=2sin 2x,f(x)=sin 2x-cos 2x=2sin=2sin 2,∴f(x)可以由g(x)向右移动个单位得到.答案 A
11、函数g(x)=sin22x的单调递增区间是( )
A.[,+](k∈Z) B.[kπ,kπ+](k∈Z)
C.[+,+](k∈Z) D.[kπ+,kπ+](k∈Z)
答案 A
12、函数f(x)=(1+cos2x)sin2x是( )
A.周期为π的奇函数 B.周期为π的偶函数 C.周期为的奇函数 D.周期为的偶函数解析 f(x)=(1+cos2x)sin2x=2cos2xsin2x=sin22x=,则T==且为偶函数.答案 D
二、填空:(4*5=20)
13、角的终边经过点且,则_____________.
解:由题意可得,求得或,
角的终边经过点且,此时.
当角的终边经过点且,此时
故答案为:或1.
14、代数式:sin2cos3tan4的符号是____________.
解:因为π=3.14所以3π/2>4>π>3>2>π/2
所以sin2>0;cos3<0;tan4>0所以sin2cos3tan4<0
15、已知,,则的值为____________.
- 11 -
解析:因为,等号两边同时平方得,即,解得,因为,则,又,所以,因此。
16、已知,sin()=- sin则cos= ____________.
解析:,,,
sin,
,即,结合,解得.
一、 解答:
17、(10分)已知:,为锐角
求
答案详解: 解析: 为锐角,,
则是锐角,,
原式
- 11 -
18(12分)已知函数的部分图象如图所示. (1)求函数的解析式;
(2)将此函数的图像向右平移后,得到g(x)的图像,试求g(x)的单调区间
解:(1)由函数的部分图象,可得, 根据,求得
再根据五点法作图可得,,
(2)略
19(12分)已知函数f(x)=cos(+x)cos(-x),g(x)=sin2x-.(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
解析 (1)f(x)=cos(+x)cos(-x)=(cosx-sinx)(cosx+sinx)=cos2x-sin2x=-=cos2x-,∴f(x)的最小正周期为=π.
(2)h(x)=f(x)-g(x)=cos2x-sin2x=cos(2x+),当2x+=2kπ(k∈Z)时,h(x)取得最大值.h(x)取得最大值时,对应的x的集合为{x|x=kπ-,k∈Z}.
20(12分)已知半径为6的圆C与x轴相切,圆心C在直线上且在第二象限,直线l过点.(Ⅰ)求圆C的方程;
(Ⅱ)若直线l与圆C相交于A、B两点且,求直线l的方程.
解:(I)由题意,设圆心圆C的半径,
又圆C和x轴相切,则
- 11 -
即,所以,所以圆C的方程为
设l方程为,由 又l方程为时也符合题意,故所求直线方程l的方程为或
21(12分)如图,在边长为1的等边△ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图所示的三棱锥A-BCF,其中BC=.
(1)证明:DE∥平面BCF. (2)证明:CF⊥平面ABF.
【解析】(1)在等边△ABC中,AD=AE,所以=,在折叠后的三棱锥A-BCF中也成立,所以DE∥BC.因为DE⊄平面BCF,BC⊂平面BCF,所以DE∥平面BCF.
(2)在等边△ABC中,F是BC的中点,所以AF⊥FC,BF=CF=.
因为在三棱锥A-BCF中,BC=,所以BC2=BF2+CF2,CF⊥BF.
因为BF∩AF=F,所以CF⊥平面ABF.
22(12分)在△ABC中,a,b,c分别是角A,B,C的对边,=(2a+c,b),=(cosB,cosC),且=0.
(1)求角B的大小.(2)设函数f(x)=sin2xcos(A+C)-cos2x,求函数f(x)的最小正周期,最大值及当f(x)取得最大值时x的值.
【解析】(1)由已知得,(2a+c)cosB+bcosC=0,即(2sinA+sinC)cosB+sinBcosC=0,
即2sinAcosB+sinCcosB+sinBcosC=0.所以2sinAcosB+sin(B+C)=0,
- 11 -
即2sinAcosB+sinA=0.因为0
查看更多