- 2021-06-16 发布 |
- 37.5 KB |
- 10页


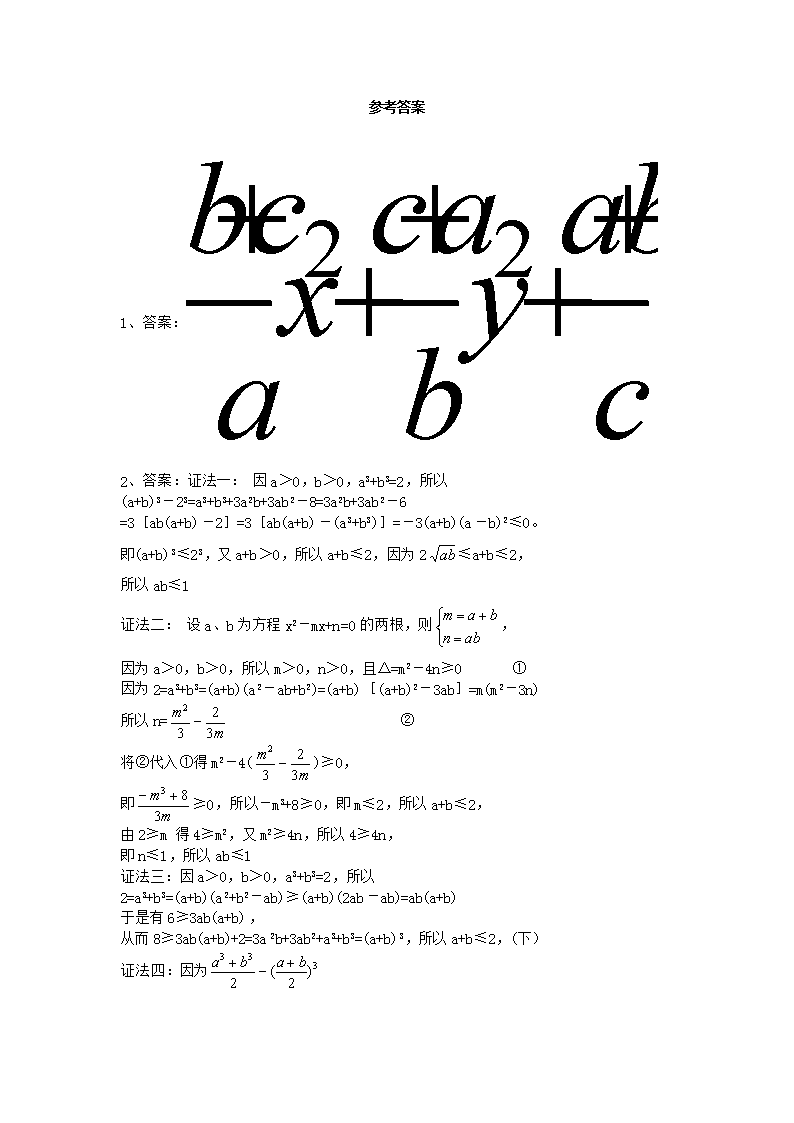
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2020届一轮复习人教A版 证明不等式的基本方法 课时作业
2020届一轮复习人教A版 证明不等式的基本方法 课时作业 1、证明下列不等式: (1)若x,y,z∈R,a,b,c∈R+,则z2≥2(xy+yz+zx) (2)若x,y,z∈R+,且x+y+z=xyz,则≥2() 2、若a>0,b>0,a3+b3=2,求证: a+b≤2,ab≤1。 3、已知i,m、n是正整数,且1<i≤m<n. (1)证明: niA<miA (2)证明: (1+m)n>(1+n)m 4、已知:,求证: (Ⅰ). (Ⅱ). 5、设,求证:。 6、设a、b、c均为实数,求证:++≥++ 7、设a,b,c为正实数.求证:+abc≥2. 8、若a,b∈R,求证:≤+. 9、设a,b,c都是正数,求证: (1)(a+b+c)≥9; (2)(a+b+c) ≥. 10、已知x1,x2,…,xn都是正数,且x1+x2+…+xn=1,求证: ++…+≥n2. 11、已知|a|<1,|b|<1,求证:<1. 12、已知x>0,y>0,z>0.求证:≥8. 13、已知,a,b,c均为正数,且a+b+c=1.求证:++≥9. 14、已知a、b∈(0,+∞),且a+b=1,求证: (1)a2+b2≥; (2)+≥8; (3)+ ≥; (4) ≥. 15、设a>0,b>0,a+b=1. (1)证明:ab+≥4; (2)探索猜想,并将结果填在以下括号内: a2b2+≥( );a3b3+≥( ); (3)由(1)(2)归纳出更一般的结论,并加以证明. 16、定义:对于函数,.若对定义域内的恒成立,则称函数为函数.(1)请举出一个定义域为的函数,并说明理由;(2)对于定义域为的函数,求证:对于定义域内的任意正数,均有; (3)对于值域的函数,求证:. 17、已知x,y均为正数,且x>y,求证:. 18、已知,且,求证: 19、已知,求证:。 20、已知都是实数,求证 参考答案 1、答案: 2、答案:证法一: 因a>0,b>0,a3+b3=2,所以 (a+b)3-23=a3+b3+3a2b+3ab2-8=3a2b+3ab2-6 =3[ab(a+b)-2]=3[ab(a+b)-(a3+b3)]=-3(a+b)(a-b)2≤0。 即(a+b)3≤23,又a+b>0,所以a+b≤2,因为2≤a+b≤2, 所以ab≤1 证法二: 设a、b为方程x2-mx+n=0的两根,则, 因为a>0,b>0,所以m>0,n>0,且Δ=m2-4n≥0 ① 因为2=a3+b3=(a+b)(a2-ab+b2)=(a+b)[(a+b)2-3ab]=m(m2-3n) 所以n= ② 将②代入①得m2-4()≥0, 即≥0,所以-m3+8≥0,即m≤2,所以a+b≤2, 由2≥m 得4≥m2,又m2≥4n,所以4≥4n, 即n≤1,所以ab≤1 证法三:因a>0,b>0,a3+b3=2,所以 2=a3+b3=(a+b)(a2+b2-ab)≥(a+b)(2ab-ab)=ab(a+b) 于是有6≥3ab(a+b), 从而8≥3ab(a+b)+2=3a2b+3ab2+a3+b3=(a+b)3,所以a+b≤2,(下) 证法四:因为 ≥0, 所以对任意非负实数a、b,有≥ 因为a>0,b>0,a3+b3=2,所以1=≥, ∴≤1,即a+b≤2,(以下) 证法五: 假设a+b>2,则 a3+b3=(a+b)(a2-ab+b2)=(a+b)[(a+b)2-3ab]>(a+b)ab>2ab,所以ab<1, 又a3+b3=(a+b)[a2-ab+b2]=(a+b)[(a+b)2-3ab]>2(22-3ab) 因为a3+b3=2,所以2>2(4-3ab),因此ab>1,前后矛盾, 故a+b≤2(以下)。 3、答案:(1)对于1<i≤m,且A =m·…·(m-i+1), , 由于m<n,对于整数k=1,2,…,i-1,有, 所以 (2)由二项式定理有: (1+m)n=1+Cm+Cm2+…+Cmn, (1+n)m=1+Cn+Cn2+…+Cnm, 由(1)知miA>niA (1<i≤m,而C= ∴miCin>niCim(1<m<n ∴m0C=n0C=1,mC=nC=m·n,m2C>n2C,…, mmC>nmC,mm+1C>0,…,mnC>0, ∴1+Cm+Cm2+…+Cmn>1+Cn+C2mn2+…+Cnm, 即(1+m)n>(1+n)m成立。 4、答案:(Ⅰ)∵,,, ∴, ∵, ∴, ∴. (Ⅱ)∵, ∴. 5、答案:因为,所以有。又,故有。 于是有 得证。 6、答案:∵a、b、c均为实数. ∴(+)≥≥,当a=b时等号成立; (+)≥≥,当b=c时等号成立; (+)≥≥. 三个不等式相加即得++≥++, 当且仅当a=b=c时等号成立. 7、答案:因为a,b,c是正实数,由平均不等式可得 ≥3, 即≥, 所以+abc≥+abc. 而+abc≥2=2, 所以+abc≥2. 8、答案:当|a+b|=0时,不等式显然成立. 当|a+b|≠0时,由0<|a+b|≤|a|+|b| ≥, 所以= ≤ = ≤+. 9、答案:(1)∵a,b,c都是正数, ∴a+b+c≥3,++≥3. ∴(a+b+c) ≥9, 当且仅当a=b=c时,等号成立. (2)∵(a+b)+(b+c)+(c+a) ≥3, 又≥, ∴(a+b+c) ≥, 当且仅当a=b=c时,等号成立. 10、答案: ++…+=(x1+x2+…+xn)( ++…+) ≥=n2. 11、答案:∵<1<1 a2+b2+2ab<1+2ab+a2b2 a2b2-a2-b2+1>0 (a2-1)(b2-1)>0 又|a|<1,|b|<1,∴(a2-1)(b2-1)>0. ∴原不等式成立. 12、答案:∵x>0,y>0,z>0, ∴+≥>0, +≥>0. +≥>0, ∴ ≥=8. (当且仅当x=y=z时等号成立) 13、答案:++= ++ =3+++ ≥3+2+2+2=9. 当且仅当a=b=c=时取等号. 14、答案:(1)∵a2+b2=(a+b)2-2ab=1-2ab≥1-2×=, ∴a2+b2≥. (2)∵+≥≥8,∴+≥8. (3)由(1)、(2)的结论,知 + =a2+b2+4++ ≥+4+8=,∴+ ≥. (4) =++ab+ =+++2≥2++2=. 15、答案:(1)证明 方法一 ab+≥44a2b2-17ab+4≥0 (4ab-1)(ab-4)≥0. ∵ab=()2≤=, ∴4ab≤1,而又知ab≤<4, 因此(4ab-1)(ab-4)≥0成立,故ab+≥4. 方法二 ab+=ab++, ∵ab≤=,∴≥4,∴≥. 当且仅当a=b=时取等号. 又ab+≥2=, 当且仅当ab=,即=4,a=b=时取等号. 故ab+≥+=4 (当且仅当a=b=时,等号成立). (2)解 猜想:当a=b=时, 不等式a2b2+≥( )与a3b3+≥( )取等号,故在括号内分别填16与64. (3)解 由此得到更一般性的结论: anbn+≥4n+. 证明如下: ∵ab≤=,∴≥4. ∴anbn+=anbn++ ≥2+×4n =+=4n+, 当且仅当ab=,即a=b=时取等号. 16、答案:(1)如函数就是定义域内的函数. 下面进行证明: 必定成立. (2)构造函数,, 即在R上递增所以, ,… 得到,, … 相加后,得到: (3)构造函数,则,因为,所以 得到有 所以,…, 所以有 17、答案:因为x>0,y>0,x-y>0, = , 所以. 18、答案:∵ --6分 又 ∴ 故 19、答案:因为 20、答案:不妨设,则 在中,由三角形三边之间的关系知: 当且仅当O在AB上时,等号成立。 因此, 查看更多