- 2021-06-16 发布 |
- 37.5 KB |
- 35页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020_2021学年新教材高中数学第五章三角函数5
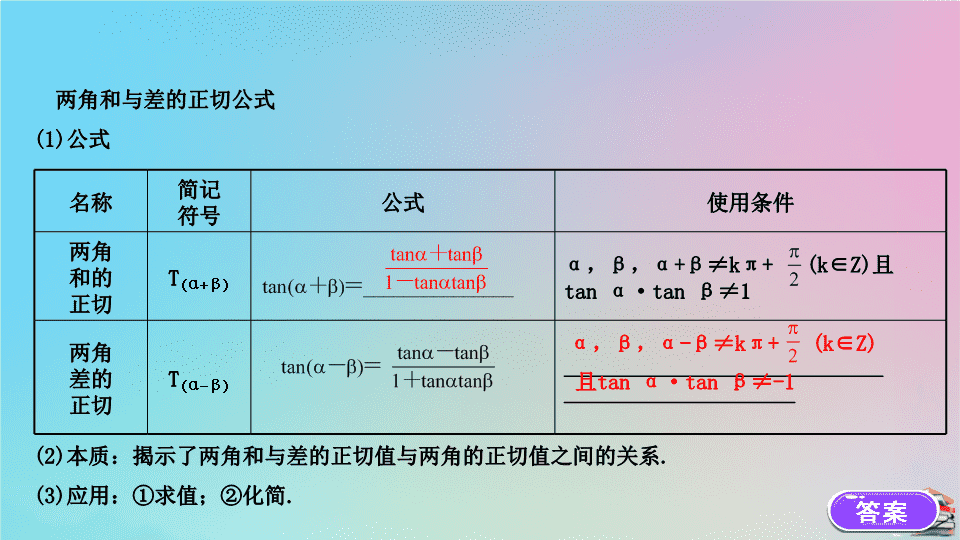
第 3 课时 两角和与差的正弦、余弦、正切公式 ( 二 ) 必备知识 · 自主学习 导思 1. 两角和与差的正切公式的形式是怎样的? 2. 两角和与差的正切公式有哪些应用? 两角和与差的正切公式 (1) 公式 (2) 本质:揭示了两角和与差的正切值与两角的正切值之间的关系 . (3) 应用:①求值;②化简 . 名称 简记 符号 公式 使用条件 两角 和的 正切 T (α+β) α , β , α+β≠kπ+ (k∈Z) 且 tan α·tan β≠1 两角 差的 正切 T (α-β) _____________________________ _____________________ α , β , α-β≠kπ+ (k∈Z) 且 tan α·tan β≠-1 【 思考 】 (1) 由同角三角函数的商数关系知 tan(α+β)= ,由此能否推导出两角 和的正切公式?若能,写出推导过程 . 提示: 能 . tan( α + β )= ,分子分母同除以 cos α cos β ,可 得 tan( α + β )= (2) 两角和与差的正切公式中为什么限制 α , β , α+β , α-β 都不等于 kπ + (k∈Z) ? 提示: 这是由正切函数的定义域决定的 . 【 基础小测 】 1. 辨析记忆 ( 对的打“√”,错的打“ ×”) (1) 存在 α , β∈R ,使 tan(α+β)=tan α+tan β 成立 . ( ) (2) 对任意 α , β∈R , tan(α+β)= 都成立 . ( ) (3)tan(α+β)= 等价于 tan α+tan β= tan( α + β )· (1-tan α tan β ).( ) 提示: (1)√. 当 α =0 , β = 时, tan( α + β )= ,但一般情况下不成立 . (2) × . 两角和的正切公式的适用范围是 α , β , α + β ≠k π + (k∈Z) 且 tan α ·tan β ≠1. (3)√. 当 α ≠k π + (k∈Z) , β ≠k π + (k∈Z) , α + β ≠k π + (k∈Z) 时, 由前一个式子两边同乘以 1-tan α tan β 可得后一个式子 . 2.( 教材二次开发:例题改编 ) 已知 cos α=- , α∈ ,则 tan = ( ) A. B.7 C.- D.-7 【 解析 】 选 B. 因为 cos α =- , α ∈ ,所以 α ∈ ,所以 sin α = - , tan α = , 则 tan 3. = ( ) 【 解析 】 选 C. 关键能力 · 合作学习 类型一 给角求值问题 ( 数学运算 ) 【 题组训练 】 1.(2019· 全国卷 Ⅰ)tan 255°= ( ) A.-2- B.-2+ C.2- D.2+ 2. 计算: =_______. 3.tan 10°+tan 50°+ tan 10°tan 50°=_______. 【 解析 】 1. 选 D.tan 255 ° =tan(180 ° +75 ° )=tan 75 ° =tan(30 ° +45 ° ) = 2. 原式 = 答案: 1 3. 因为 tan 60 ° =tan(10 ° +50 ° )= 所以 tan 10 ° +tan 50 ° =tan 60 ° (1-tan 10 ° tan 50 ° ) = - tan 10 ° tan 50 ° ,所以原式 = - tan 10 ° tan 50 ° + tan 10 ° tan 50 ° = . 答案: 【 解题策略 】 公式 T (α+β) , T (α-β) 应用的解题策略 (1) 公式 T (α+β) , T (α-β) 有 tan α·tan β , tan α+tan β( 或 tan α-tan β) , tan(α+β)( 或 tan(α-β)) ,三者知二可求出第三个 . (2) 化简过程中注意“ 1” 与“ tan ” ,“ ”与“ tan ” 等特殊数与特殊 角的函数值之间的转化 . 【 补偿训练 】 tan 72°-tan 42°- tan 72°tan 42°=_______. 【 解析 】 原式 =tan(72 ° -42 ° )(1+tan 72 ° ·tan 42 ° )- tan 72 ° tan 42 ° =tan 30 ° (1+tan 72 ° tan 42 ° )-tan 30 ° tan 72 ° tan 42 ° =tan 30 ° = . 答案: 类型二 给值求角问题 ( 数学运算 ) 【 典例 】 (2020· 洛阳高一检测 ) 已知 tan =2 , tan(α-β)= , α∈ (1) 求 tan α 的值; (2) 求 2α-β 的值 . 【 解题策略 】 给值求角问题的步骤及选取函数的原则 (1) 给值求角问题的步骤 . ① 求所求角的某个三角函数值 . ② 确定所求角的范围 ( 范围过大或过小,会使求出的角不合题意或漏解 ) ,根据 范围找出角 . (2) 选取函数的原则 . ① 已知正切函数值,选正切函数 . ② 已知正余弦函数值,选正弦或余弦函数,若角的范围是 ,选正弦或余弦 函数均可;若角的范围是 (0 , π) ,选余弦较好;若角的范围是 ,选正弦 较好 . 【 跟踪训练 】 已知 tan α= , sin β= ,且 α , β 为锐角,求 α+2β 的值 . 【 解析 】 因为 tan α = <1 且 α 为锐角, 所以 0< α < . 又因为 sin β = 且 β 为锐角 . 所以 0< β < , 所以 0< α +2 β < . ① 由 sin β = , β 为锐角,得 cos β = , 所以 tan β = . 所以 tan( α + β )= 所以 tan( α +2 β )= 由 ①② 可得 α +2 β = . 【 补偿训练 】 已知 α , β , γ 都是锐角,且 tan α= , tan β= , tan γ= ,则 α+β+γ=_______. 【 解析 】 因为 tan( α + β )= tan( α + β + γ )= 因为 tan α = ,且 α 为锐角, 所以 0< α < ,同理 0< β < , 0< γ < , 所以 0< α + β + γ < ,所以 α + β + γ = . 答案: 类型三 给值求值问题 ( 数学运算 ) 角度 1 式子变换 【 典例 】 已知 sin α= , α∈ , tan(π-β)= ,则 tan(α-β) 的值 为 ( ) 【 思路导引 】 由条件得出 tan α 与 tan β 的值,代入两角差的正切公式可求值 . 【 解析 】 选 A. 因为 α ∈ , sin α = , 所以 cos α =- , tan α =- ,又 tan β =- , 所以 tan( α - β )= 【 变式探究 】 本例条件不变,求 tan(α+β) 的值 . 【 解析 】 因为 α ∈ , sin α = ,所以 cos α =- , tan α =- ,又 tan β =- , 所以 tan( α + β )= 角度 2 拆角变换 【 典例 】 已知 tan α= , tan(α-β)=- ,那么 tan(β-2α) 的值为 ( ) 【 思路导引 】 tan(β-2α)=-tan(2α-β)=-tan 【 解析 】 选 B.tan( β -2 α )=-tan(2 α - β ) 【 解题策略 】 给值求值问题的两种变换 (1) 式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式子间的联系以实现求值 . (2) 角的变换:首先从已知角间的关系入手,分析已知角与待求角间的关系,如用 α=β-(β-α) 、 2α=(α+β)+(α-β) 等关系,把待求的三角函数与已知三角函数巧妙地建立等量关系,从而求值 . 【 题组训练 】 1. 若 tan α=2 , tan β= ,则 tan(α+β) 等于 ( ) A.1 B.-1 C.7 D.-7 【 解析 】 选 C.tan( α + β )= 2. 已知 tan ,则 tan(α+β) 的值为 ( ) 【 解析 】 选 D. 因为 tan 所以 tan( α + β ) 课堂检测 · 素养达标 1. 已知 tan α=- ,则 tan 等于 ( ) A.- B.-7 C. D.7 【 解析 】 选 D.tan 2.tan α=2 , tan β=3 ,则 tan(α-β)= ( ) A.-7 B. C.- D.- 【 解析 】 选 D.tan( α - β )= 3. 已知 α , β 都是锐角, tan α= , tan β= ,则 α+β 的值为 ( ) 【 解析 】 选 C.tan( α + β )= 又因为 α , β 都是锐角,所以 α + β ∈(0 , π ) ,所以 α + β = . 4.( 教材二次开发:练习改编 ) 求值: (1)tan(-75°)=_______ ; (2) =_______. 【 解析 】 (1)tan 75 ° =tan(45 ° +30 ° )= 所以 tan(-75 ° )=-tan 75 ° =-2- . (2) 原式 =tan(74 ° +76 ° )=tan 150 ° =- . 答案: (1)-2- (2)- 5. 计算 =_______. 【 解析 】 答案: 1查看更多