【数学】2020届一轮复习（文理合用）第10章计数原理、概率、随机变量及其分布（理）作业

【数学】2020届一轮复习（文理合用）第10章计数原理、概率、随机变量及其分布（理）作业

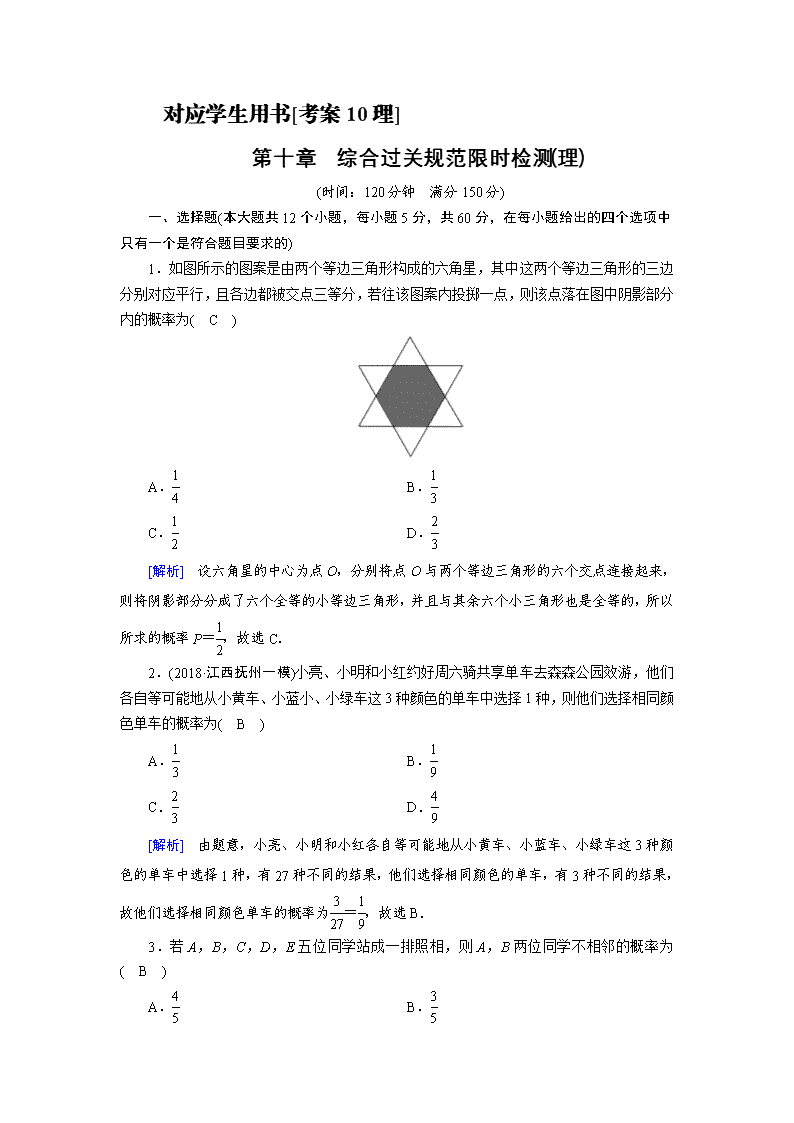
对应学生用书[考案10理]　‎ 第十章　综合过关规范限时检测(理)‎ ‎(时间：120分钟　满分150分)‎ 一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的)‎ ‎1．如图所示的图案是由两个等边三角形构成的六角星，其中这两个等边三角形的三边分别对应平行，且各边都被交点三等分，若往该图案内投掷一点，则该点落在图中阴影部分内的概率为(　C　)‎ A．　　 B． C．　　 D． ‎[解析]　设六角星的中心为点O，分别将点O与两个等边三角形的六个交点连接起来，则将阴影部分分成了六个全等的小等边三角形，并且与其余六个小三角形也是全等的，所以所求的概率P＝，故选C．‎ ‎2．(2018·江西抚州一模)小亮、小明和小红约好周六骑共享单车去森森公园效游，他们各自等可能地从小黄车、小蓝小、小绿车这3种颜色的单车中选择1种，则他们选择相同颜色单车的概率为(　B　)‎ A．　　 B．　　‎ C．　　 D． ‎[解析]　由题意，小亮、小明和小红各自等可能地从小黄车、小蓝车、小绿车这3种颜色的单车中选择1种，有27种不同的结果，他们选择相同颜色的单车，有3种不同的结果，故他们选择相同颜色单车的概率为＝，故选B．‎ ‎3．若A，B，C，D，E五位同学站成一排照相，则A，B两位同学不相邻的概率为(　B　)‎ A．　　 B．　　‎ C．　　 D． ‎[解析]　A，B，C，D，E五位同学站成一排照相的总结果数为A＝120，先排C，D，E三位同学，再在形成的4个“空”中排A，B两位同学，有A×A＝72(种)排法，故所求的概率为＝，选B．‎ ‎4．(2018·江西上高二中月考)有一批产品，其中有12件正品和4件次品，从中有放回地任取3件．若ξ表示取到次品的个数，则D(ξ)＝(　C　)‎ A．　　 B．　　‎ C．　　 D． ‎[解析]　由题意，得次品率P＝＝，则ξ～B(3，)，所以D(ξ)＝3××(1－)＝.故选C．‎ ‎5．(2018·海南模拟)某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是(　A　)‎ A．0.8　　 B．0.75　　‎ C．0.6　　 D．0.45‎ ‎[解析]　根据条件概率公式，直接代入，可求得随后一天的空气质量为优良的概率，已知连续两天为优良的概率是0.6，那么在前一天空气质量为优良的前提下，要求随后一天的空气质量为优良的概率，可根据条件概率公式，得P＝＝0.8.‎ ‎6．(2018·河南濮阳模拟)在[－6,9]内任取一个实数m，设f(x)＝－x2＋mx＋m，则函数f(x)的图象与x轴有公共点的概率等于(　D　)‎ A．　　 B．　　‎ C．　　 D． ‎[解析]　∵f(x)＝－x2＋mx＋m的图象与x轴有公共点，∴Δ＝m2＋4m>0，∴m<－4或m>0，∴在[－6,9]内取一个实数m，函数f(x)的图象与x轴有公共点的概率P＝＝，故选D．‎ ‎7．如图，在平面直角坐标系xOy中，O为正十边形A1A2A3…A10的中心，A1在x轴正半轴上，任取不同的两点Ai，Aj(其中1≤i，j≤10，且i∈N，j∈N)，点P满足2＋＋＝0，则点P落在第二象限的概率是(　B　)‎ A．　　 B．　　‎ C．　　 D． ‎[解析]　在正十边形A1A2A3…A10的十个顶点中任取两个，不同的取法有C＝45(种)，满足2＋＋＝0，且点P落在第二象限的不同取法有(A1，A7)，(A1，A8)，(A1，A9)，(A1，A10)，(A2，A8)，(A2，A9)，(A8，A10)，(A9，A10)，共8种，所以点P落在第二象限的概率为，故选B．‎ ‎8．二项式(－2x2)9的展开式中，除常数项外，各项系数的和为(　B　)‎ A．－671　　 B．671　　‎ C．672　　 D．673‎ ‎[解析]　令x＝1，可得该二项式的展开式中，各项系数之和为－1.因为该二项展开式的通项公式为Tr＋1＝C()9－r·(－2x2)r＝C(－2)r·x3r－9，令3r－9＝0，得r＝3，所以该二项展开式中的常数项为C(－2)3＝－672，所以除常数项外，各项系数的和为－1－(－672)＝671，故选B．‎ ‎9．(2018·课标Ⅰ卷)下图来自古希腊数学家希波克拉底所研究的几何图形．此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC.△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ.在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为p1，p2，p3，则(　A　)‎ A．p1＝p2　　 B．p1＝p3‎ C．p2＝p3　　 D．p1＝p2＋p3‎ ‎[解析]　设AB＝c，AC＝b，则区域Ⅰ的面积S1＝bc；区域Ⅲ的面积S3＝π(b2＋c2)－bc，区域Ⅱ的面积S2＝π(b2＋c2)－S3＝bc＝S1，由几何概型可知p1＝p2，故选A．‎ ‎10．旅游体验师小明受某网站邀请，决定对甲、乙、丙、丁这四个景区进行体验式旅游，若不能最先去甲景区旅游，不能最后去乙景区和丁景区旅游，则小李可选的旅游路线数为(　D　)‎ A．24　　 B．18　　‎ C．16　　 D．10‎ ‎[解析]　分两种情况，第一种：最后体验甲景区，则有A种可选的路线；第二种：不在最后体验甲景区，则有C·A种可选的路线．所以小李可选的旅游路线数为A＋C·A＝10.选D．‎ ‎11．已知某公司生产的一种产品的质量X(单位：克)服从正态分布N(100,4)．现从该产品的生产线上随机抽取10000件产品，其中质量在[98,104]内的产品估计有 附：若X服从正态分布N(μ，σ2)，则P(μ－σ6.635，‎ 所以有99%的把握认为是否爱好该项运动与性别有关．‎ ‎(3)由题意，抽取6人中包括男生4名，女生2名，X的取值为0,1,2，则P(X＝0)＝＝，P(X＝1)＝＝，P(X＝2)＝＝，‎ 故X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P E(X)＝0×＋1×＋2×＝1.‎ ‎18．(本题满分15分)(2019·江西南昌模拟)甲、乙两人进行围棋比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满8局时停止．设甲在每局中获胜的概率为P(P>)，且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为.‎ ‎(1)求P的值；‎ ‎(2)设ξ表示比赛停止时已比赛的局数，求随机变量ξ的分布列和数学期望E(ξ)．‎ ‎[解析]　(1)依题意，当甲连胜2局或乙连胜2局时，第二局比赛结束时比赛停止，∴P2＋(1－P)2＝，‎ 解得P＝或P＝.∵P>，∴P＝.‎ ‎(2)依题意知，ξ的所有可能值为2,4,6,8.‎ 设每两局比赛为一轮，则该轮结束时比赛停止的概率为.若该轮结束时比赛还将继续，则甲、乙在该轮中必是各得一分，此时，该轮比赛结果对下轮比赛是否停止没有影响，‎ 从而有P( ξ＝2)＝，P(ξ＝4)＝(1－)×＝，‎ P(ξ＝6)＝(1－)(1－)×＝，‎ P(ξ＝8)＝(1－)(1－)(1－)×1＝，‎ ‎∴随机变量ξ的分布列为 ξ ‎2‎ ‎4‎ ‎6‎ ‎8‎ P 故E(ξ)＝2×＋4×＋6×＋8×＝.‎ ‎19．(本题满分15分)(2019·辽宁盘锦模拟)某校为了解甲、乙两班学生的学业水平，从两班中各随机抽取20人参加学业水平等级考试，得到学生的学业成绩茎叶图如图：‎ ‎(1)通过茎叶图比较甲、乙两班学生的学业成绩平均值甲与乙及方差s与s的大小；(只需写出结论)‎ ‎(2)根据学生的学业成绩，将学业水平分为三个等级：‎ 学业成绩 低于70分 ‎70分到89分 不低于90分 学业水平 一般 良好 优秀 根据所给数据，频率可以视为相应的概率．‎ ‎①从甲、乙两班中各随机抽取1人，记事件C：“抽到的甲班学生的学业水平等级高于乙班学生的学业水平等级”，求C发生的概率；‎ ‎②从甲班中随机抽取2人，记X为学业水平优秀的人数，求X的分布列和数学期望．‎ ‎[解析]　(1)甲>乙；SE(ξ1)，所以－10p2＋10p＋117.6>120，解得0.4

查看更多