20届 湖北省高三（5月）调研模拟考试 （理 数）

20届 湖北省高三（5月）调研模拟考试 （理 数）

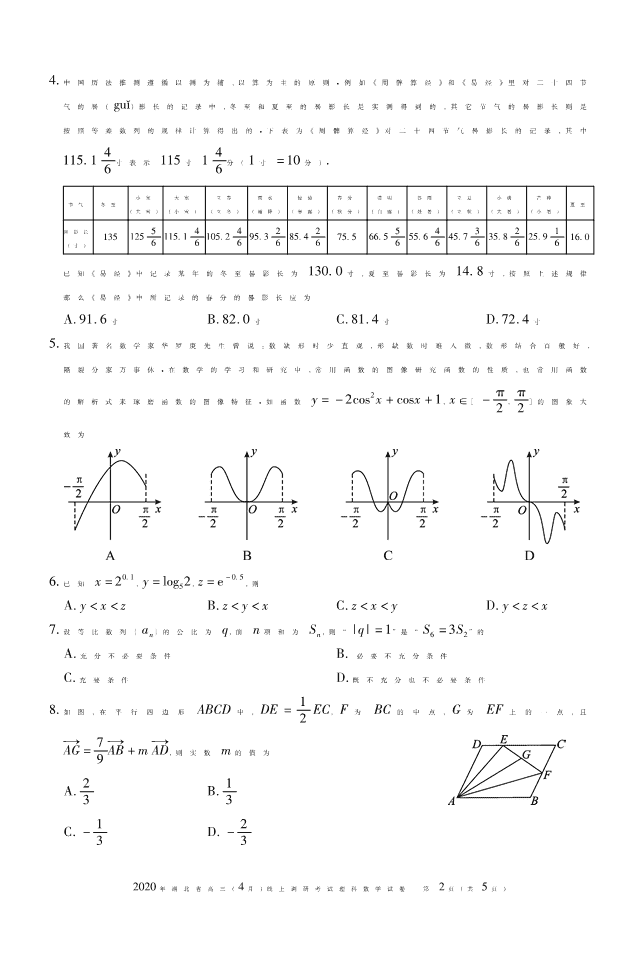
书书书 ２０２０年湖北省高三（４月）线上调研考试 理 科 数 学 试 卷 ２０２０．４ 本试卷共 ５页，２３题（含选考题）。全卷满分 １５０分。考试用时 １２０分钟。 ★祝考试顺利★ 注意事项： １．考试过程中，请考生自觉遵守考试纪律等相关规定，诚信应考，不得有作弊、泄露试题等行为。请家 长做好监考工作。 ２．请确保网络环境、考试环境良好，备好答题所用的白纸和笔。 ３．登录好分数 ＡＰＰ，点击“作业测试”，进入对应考试科目。“试卷”将根据考试时间准时显示。开考 后，考生首先在白纸上手写答题。答题结束后，点击“填写答题卡”，进入到“在线答题卡”。将事先准备好 的答案，填写至在线答题卡上（选择题、多选题及判断题，直接在“在线答题卡”上勾选答案；主观题按照要 求将手写的答案竖向拍照，并分别上传），然后点击“提交答题卡”完成提交。答题卡上传提交后考试时间 范围内还能继续提交覆盖，为了避免大家都在考试最后快结束的时间上传造成拥堵，建议提前上传。 备注：主观题要确保答案及照片清晰、干净、完整；为留取拍照时间，考试将延长 １０分钟。 ４．此次全省联考是检测复课前线上备考成效的一次重要考试，有利于调整和优 化复课后备考策略，请考生和家长高度重视。考试结束后，考试组织方将为所有考生 免费提供《考试成绩和学情分析报告》。请考生或家长及时扫描右方二维码，关注“育 路通”微信公众号。依次点击“高考测评—查看报告”，即可免费查询。 一、选择题：本大题共 １２小题，每小题 ５分，共 ６０分．在每小题给出的四个选项中，只有一项 是符合题目要求的． １．已知实数集 Ｒ，集合 Ａ＝｛ｘ｜－１＜ｘ＜５｝，集合 Ｂ＝｛ｙ｜ｙ＝ １ ｘ槡 －２ ｝，则 Ａ∩（瓓ＲＢ）＝ Ａ．｛ｘ｜－１＜ｘ≤２｝ Ｂ．｛ｘ｜ｘ＞－１｝ Ｃ．｛ｘ｜－１＜ｘ≤０｝ Ｄ．｛ｘ｜０≤ｘ＜５｝ ２．已知 ｚ∈Ｃ，若｜ｚ｜－珋ｚ＝１＋２ｉ，则 Ｚ＝ Ａ．３ ２－２ｉ Ｂ．３ ２＋２ｉ Ｃ．－３ ２－２ｉ Ｄ．－３ ２＋２ｉ ３．若（１－２ｘ）２０２０＝ａ０＋ａ１ｘ＋ａ２ｘ２＋… ＋ａ２０２０ｘ２０２０，则 ａ１＋ａ２＋ａ３＋… ＋ａ２０２０＝ Ａ．０ Ｂ．１ Ｃ．－１ Ｄ．２ ２０２０年湖北省高三（４月）线上调研考试理科数学试卷　第 １页（共 ５页） ４．中国历法推测遵循以测为辅、以算为主的原则．例如《周髀算经》和《易经》里对二十四节 气的晷（ｇｕǐ）影长的记录中，冬至和夏至的晷影长是实测得到的，其它节气的晷影长则是 按照等差数列的规律计算得出的．下表为《周髀算经》对二十四节气晷影长的记录，其中 １１５．１４ ６寸表示 １１５寸 １４ ６分（１寸 ＝１０分）． 节气 冬至 小寒 （大雪） 大寒 （小雪） 立春 （立冬） 雨水 （霜降） 惊蛰 （寒露） 春分 （秋分） 清明 （白露） 谷雨 （处暑） 立夏 （立秋） 小满 （大暑） 芒种 （小暑） 夏至 晷影长 （寸） １３５ １２５ ５ ６ １１５．１ ４ ６ １０５．２ ４ ６ ９５．３ ２ ６ ８５．４ ２ ６ ７５．５ ６６．５ ５ ６ ５５．６ ４ ６ ４５．７ ３ ６ ３５．８ ２ ６ ２５．９ １ ６ １６．０ 已知《易经》中记录某年的冬至晷影长为 １３０．０寸，夏至晷影长为 １４．８寸，按照上述规律 那么《易经》中所记录的春分的晷影长应为 Ａ．９１．６寸 Ｂ．８２．０寸 Ｃ．８１．４寸 Ｄ．７２．４寸 ５．我国著名数学家华罗庚先生曾说：数缺形时少直观，形缺数时难入微，数形结合百般好， 隔裂分家万事休．在数学的学习和研究中，常用函数的图像研究函数的性质，也常用函数 的解析式来琢磨函数的图像特征．如函数 ｙ＝－２ｃｏｓ２ｘ＋ｃｏｓｘ＋１，ｘ∈［－π ２，π ２］的图象大 致为 ６．已知 ｘ＝２０．１，ｙ＝ｌｏｇ５２，ｚ＝ｅ－０．５，则 Ａ．ｙ＜ｘ＜ｚ Ｂ．ｚ＜ｙ＜ｘ Ｃ．ｚ＜ｘ＜ｙ Ｄ．ｙ＜ｚ＜ｘ ７．设等比数列｛ａｎ｝的公比为 ｑ，前 ｎ项和为 Ｓｎ，则“｜ｑ｜＝１”是“Ｓ６＝３Ｓ２”的 Ａ．充分不必要条件 Ｂ．必要不充分条件 Ｃ．充要条件 Ｄ．既不充分也不必要条件 ８．如图，在平行四边形 ＡＢＣＤ中，ＤＥ＝１ ２ＥＣ，Ｆ为 ＢＣ的 中 点，Ｇ为 ＥＦ上 的 一 点，且 →ＡＧ＝７ ９ →ＡＢ＋ →ｍＡＤ，则实数 ｍ的值为 Ａ．２ ３ Ｂ．１ ３ Ｃ．－１ ３ Ｄ．－２ ３ ２０２０年湖北省高三（４月）线上调研考试理科数学试卷　第 ２页（共 ５页） ９．已知函数 ｆ（ｘ）＝ －ｘ２＋ａｘ，ｘ≤１ ３ａｘ－７，ｘ{ ＞１ ，若存在 ｘ１，ｘ２∈Ｒ，且 ｘ１≠ｘ２，使得 ｆ（ｘ１）＝ｆ（ｘ２）成立，则 实数 ａ的取值范围是 Ａ．（－２，２） Ｂ．（－２，２］ Ｃ．（－∞，３） Ｄ．（－∞，３］ １０．已知双曲线 Ｃ：ｘ２ ａ２ －ｙ２ ｂ２ ＝１（ａ＞０，ｂ＞０）的左右焦点分别为 Ｆ１，Ｆ２，过 Ｆ１的直线与 Ｃ的两 条渐近线分别交于 Ａ、Ｂ两点，若以 Ｆ１Ｆ２为直径的圆过点 Ｂ，且 Ａ为 Ｆ１Ｂ的中点，则 Ｃ的 离心率为 槡 槡 槡Ａ．３＋１ Ｂ．２ Ｃ．３ Ｄ．２ １１．一竖立在水平地面上的圆锥形物体的母线长为 ２ｍ，一只蚂蚁从圆锥的底面圆周上的点 Ｐ出发，绕圆锥表面爬行一周后回到 Ｐ点，蚂蚁爬行的最短路径为 槡２ ３ｍ，则圆锥的底面 圆半径为 Ａ．２ ３ｍ Ｂ．１ｍ Ｃ．４ ３ｍ Ｄ．３ ２ｍ １２．已知函数 ｆ（ｘ）＝ｃｏｓ（ωｘ－２π ３）（ω＞０），ｘ１，ｘ２，ｘ３∈ ［０，π］，且 ｘ∈ ［０，π］都 有 ｆ（ｘ１）≤ｆ（ｘ）≤ｆ（ｘ２），满足 ｆ（ｘ３）＝０的实数 ｘ３有且只有 ３个．则下述四个结论： ①满足题目条件的实数 ｘ１有且只有一个；　②满足题目条件的实数 ｘ２有且只有一个； ③ｆ（ｘ）在上（０，π １０）单调递增；　④ω的取值范围是［１３ ６，１９ ６）． 其中正确结论的编号是 Ａ．①④ Ｂ．①③④ Ｃ．②③ Ｄ．①②③ 二、填空题：本大题共 ４小题，每小题 ５分，共 ２０分． １３．设曲线 ｙ＝ｅｘ＋１上点 Ｐ处的切线平行于直线 ｘ－ｙ－１＝０，则点 Ｐ的坐标是 ． １４．某学校选拔新生补进“篮球”、“电子竞技”、“国学”三个社团，根据资料统计，新生通过 考核选拔进入这三个社团成功与否相互独立．２０１９年某新生入学，假设他通过考核选 拔进入该校“篮球”、“电子竞技”、“国学”三个社团的概率依次为 ｍ，１ ３，ｎ，已知这三个 社团他都能进入得概率为 １ ２４，至少进入一个社团的概率为 ３ ４，则 ｍ＋ｎ＝ ． １５．自湖北爆发新型冠状病毒肺炎疫情以来，湖北某市医护人员和医疗、生活物资严重匮 乏，全国各地纷纷驰援．某运输队接到从武汉送往该市物资的任务，该运输队有 ８辆载重 为 ６ｔ的 Ａ型卡车，６辆载重为 １０ｔ的 Ｂ型卡车，１０名驾驶员，要求此运输队每天至少运 送 ２４０ｔ物资．已知每辆卡车每天往返的次数为 Ａ型卡车 ５次，Ｂ型卡车 ４次，每辆卡车 每天往返的成本 Ａ型卡车 １２００元，Ｂ型卡车 １８００元，则每天派出运输队所花的成本最 低为 ． ２０２０年湖北省高三（４月）线上调研考试理科数学试卷　第 ３页（共 ５页） １６．已知椭圆 ｘ２ ２ ＋ｙ２ ＝１的左、右焦点分别为 Ｆ１，Ｆ２，Ｍ 为椭圆上异于长轴端点的动点， △ＭＦ１Ｆ２的内心为 Ｉ，则 →ＭＩ·ＭＦ→ ２ ｜ＭＦ→ ２｜ ＝ ． 三、解答题：共 ７０分．解答应写出文字说明、证明过程或演算步骤．第 １７题 ～第 ２１题为必考 题，每个试题考生都必须作答．第 ２２题 ～第 ２３题为选考题，考生根据要求作答． （一）必考题：共 ６０分． １７．（本小题满分 １２分） 在△ＡＢＣ中，角 Ａ、Ｂ、Ｃ所对的边为 ａ、ｂ、ｃ，且 满 足 ｃｏｓ２Ａ－ｃｏｓ２Ｂ＝２ｓｉｎ（π ３ ＋Ａ） ｓｉｎ（π ３－Ａ）． （１）求角 Ｂ的值； （２）若 ｂ 槡＝ ３≤ａ，求 ａ－１ ２ｃ的取值范围． １８．（本小题满分 １２分） 如图，在四棱锥 Ｓ－ＡＢＣＤ中，侧面 ＳＣＤ为钝角三角形且垂直于底面 ＡＢＣＤ，ＣＤ＝ＳＤ，点 Ｍ是 ＳＡ的中点，ＡＤ∥ＢＣ，∠ＡＢＣ＝９０°，ＡＢ＝ＡＤ＝１ ２ＢＣ． （１）求证：ＢＤ⊥平面 ＳＣＤ； （２）若直线 ＳＤ与底面 ＡＢＣＤ所成的角为 ６０°，求平面 ＭＢＤ 与平面 ＳＢＣ所成的锐二面角的余弦值． １９．（本小题满分 １２分） 线段 ＡＢ为圆 Ｍ：ｘ２＋ｙ２＋２ｘ－１０ｙ＋６＝０的一条直径，其端点 Ａ，Ｂ在抛物线 Ｃ：ｘ２ ＝２ｐｙ （ｐ＞０）上，且 Ａ，Ｂ两点到抛物线 Ｃ焦点的距离之和为 １１． （１）求抛物线 Ｃ的方程及直径 ＡＢ所在的直线方程； （２）过 Ｍ点的直线 ｌ交抛物线 Ｃ于 Ｐ，Ｑ两点，!物线 Ｃ在 Ｐ，Ｑ处的切线相交于 Ｎ点， 求△ＰＱＮ面积的取值范围． ２０．（本小题满分 １２分） 已知函数 ｆ（ｘ）＝ｘ２＋πｃｏｓｘ． （１）求函数 ｆ（ｘ）的最小值； （２）若函数 ｇ（ｘ）＝ｆ（ｘ）－ａ在（０，＋∞）上有两个零点 ｘ１，ｘ２，且 ｘ１ ＜ｘ２ "求证： ｘ１＋ｘ２＜π． ２０２０年湖北省高三（４月）线上调研考试理科数学试卷　第 ４页（共 ５页） ２１．（本小题满分 １２分） ２０２０年春节期间爆发的新型冠状病毒（２０１９－ｎＣｏＶ），是一种可以借助飞沫和接触传 播的变异病毒。某定点医院为筛查某些人是否感染该病毒，需要检验血液是否为阳性，现 有 ｎ份血液样本，有以下两种检验方式： （ａ）逐份检验，则需要检验 ｎ次； （ｂ）混合检验，将其中 ｋ（ｋ∈Ｎ 且 ｋ≥２）份血液样本分别取样混合在一起检验．若检验 结果为阴性，这 ｋ份的血液全为阴性，因而这 ｋ份血液样本只要检验一次就够了；如果检验 结果为阳性，为了明确这 ｋ份血液究竟哪几份为阳性，就要对这这 ｋ份再逐份检验，此时这 ｋ份血液的检验次数总共为 ｋ＋１次．假设在接受检验的血液样本中，每份样本的检验结果 是阳性还是阴性都是独立的，且每份样本是阳性结果的概率为 ｐ（０＜ｐ＜１）． （１）假设有 ６份血液样本，其中只有 ２份样本为阳性，若采用逐份检验方式，求恰好经 过 ４次检验就能把阳性样本全部检验出来的概率； （２）现取其中 ｋ（ｋ∈Ｎ 且 ｋ≥２）份血液样本，记采用逐份检验方式，样本需要检验的总 次数为 ξ１，采用混合检验方式，样本需要检验的总次数为 ξ２． （ｉ）试运用概率统计的知识，若 Ｅξ１＝Ｅξ２，试求 ｐ关于 ｋ的函数关系式 ｐ＝ｆ（ｋ）； （ｉｉ）若 ｐ＝１－ｅ－１ ４，采用混合检验方式可以使得样本需要检验的总次数的期望值比逐 份检验的总次数期望值更小，求 ｋ的最大值． 参考数据：ｌｎ２≈０．６９３１，ｌｎ３≈１．０９８６，ｌｎ５≈１．６０９４，ｌｎ７≈１．９４５９ （二）选考题：共 １０分．请考生在 ２２，２３题中任选一题作答．如果多做，则按所做的第一题计 分．作答时写清题号． ２２．［选修 ４－４：坐标系与参数方程］（１０分） 在平面直角坐标系 ｘＯｙ中，曲线 Ｃ１ 的参数方程为 ｘ＝２＋２ｃｏｓθ ｙ＝２ｓｉｎ{ θ （θ为参数），以原点为 极点，ｘ轴非负半轴为极轴，建立极坐标系，曲线 Ｃ２的极坐标方程为 ρ２＝ ４ １＋３ｓｉｎ２α． （１）求曲线 Ｃ１的极坐标方程以及曲线 Ｃ２的直角坐标方程； （２）若直线 ｌ：ｙ＝ｋｘ与曲线 Ｃ１、曲线 Ｃ２在第一象限交于 Ｐ，Ｑ，且 ｜ＯＱ｜＝｜ＰＱ｜，点 Ｍ的 直角坐标为（１，０），求△ＰＭＱ的面积． ２３．［选修 ４－５：不等式选讲］（１０分） 已知实数 ａ，ｂ满足 ａ２＋ｂ２－ａｂ＝３． （１）求 ａ－ｂ的取值范围； （２）若 ａｂ＞０，求证：１ ａ２ ＋１ ｂ２ ＋３ ４≥ ４ ａｂ． ２０２０年湖北省高三（４月）线上调研考试理科数学试卷　第 ５页（共 ５页）