- 2021-06-16 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
河北武邑中学2019—2020学年高三年级上学期期中考试数学试题(理)定稿
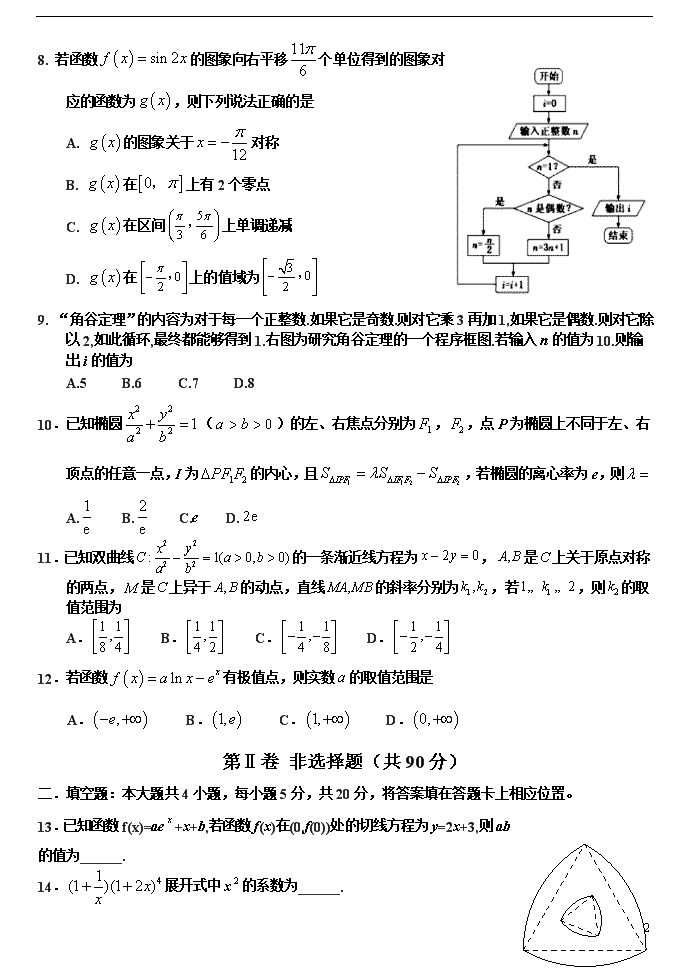
1 河北武邑中学 2019—2020 学年高三年级下学期期中考试 数学试题(理科) 注意事项: 1.本试卷分第Ⅰ卷(选择题)和 II 卷(非选择题)两部分,满分150 分,考试时间120 分钟。 2.答题前请仔细阅读答题卡(纸)上的“注意事项”,按照“注意事项”的规定答题。 3.选择题答案涂在答题卡上,非选择题答案写在答题卡上相应位置,在试卷和草稿纸上作答无效。 第Ⅰ卷 选择题(共 60 分) 一.选择题:本题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,有且只有一项符 合题目要求,将正确答案填涂在答题卡上。 1.已知集合 , | 2 0A x y x y , , | 1 0B x y x my .若 A B ,则实数 m A. 2 B. 1 2 C. 1 2 D. 2 2.设复数 z 满足 1 iz z (i 为虚数单位), z 在复平面内对应的点为( x , y ),则 A. y x B. y x C. 2 21 1 1x y D. 2 21 1 1x y 3.已知两个单位向量 1 2,e e ,若 1 2 12 e e e ,则 1 2,e e 的夹角为 A. B. C. D. 4.某学校拟从甲、乙等 5 位同学中随机选派 3 人去参加国防教育活动,则甲、乙均被选中的概率为 A. 3 5 B. 1 2 C. 2 5 D. 3 10 5.已知点 ,P x y 满足不等式 3 2 0 5 0 5 0 x y x y x ,点 ,Q x y 是函数 2( ) 1f x x 的图像上任意一点, 则两点 P,Q 之间距离的最小值为 A. 5 2 12 B. 13 1 C.4 D. 5 2 2 6.若 3 3 12 3 1log e,2 e,a b c ,则 A. a b c B. c a b C. a c b D. c b a 7.若 tan 3cos( )2 ,则 cos2 A. 1 B. 7 9 C. 0 或 7 9 D. 1 或 7 9 2 8. 若函数 sin 2f x x 的图象向右平移11 6 个单位得到的图象 对应的函数为 g x ,则下列说法正确的是 A. g x 的图象关于 12x 对称 B. g x 在 0 , 上有 2 个零点 C. g x 在区间 5 3 6 , 上单调递减 D. g x 在 02 , 上的值域为 3 02 , 9. “角谷定理”的内容为对于每一个正整数.如果它是奇数.则对它乘 3 再加 1,如果它是偶数.则对它除 以 2,如此循环,最终都能够得到 1.右图为研究角谷定理的一个程序框图.若输入 n 的值为 10.则输出 i 的值为 A.5 B.6 C.7 D.8 10.已知椭圆 2 2 2 2 1x y a b ( 0a b )的左、右焦点分别为 1F , 2F ,点 P 为椭圆上不同于左、右 顶点的任意一点,I 为 1 2PF F 的内心,且 1 1 2 2IPF IF F IPFS S S ,若椭圆的离心率为 e,则 A. 1 e B. 2 e C.e D. 2e 11.已知双曲线 2 2 2 2: 1( 0, 0)x yC a ba b 的一条渐近线方程为 2 0x y , ,A B 是C 上关于原点对称 的两点, M 是 C 上异于 ,A B 的动点,直线 ,MA MB 的斜率分别为 1 2,k k ,若 11 2k ,则 2k 的取 值范围为 A. 1 1,8 4 B. 1 1,4 2 C. 1 1,4 8 D. 1 1,2 4 12.若函数 ln xf x a x e 有极值点,则实数 a 的取值范围是 A. ,e B. 1,e C. 1, D. 0, 第Ⅱ卷 非选择题(共 90 分) 二.填空题:本大题共 4 小题,每小题 5 分,共 20 分,将答案填在答题卡上相应位置。 13.已知函数 f(x)=ae x +x+b,若函数 f(x)在(0,f(0))处的切线方程为 y=2x+3,则 ab 的值为______. 14. 41(1 )(1 2 )xx 展开式中 x 2 的系数为______. 3 15.勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先 发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三 段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的 边长比为1:3 ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______. 16.平行四边形 ABCD 中, ABD 是腰长为 2 的等腰直角三角形, 90ABD ,现将 ABD 沿 BD 折起,使二面角 A BD C 大小为 2 3 ,若 A,B,C,D 四点在同一球面上,则该球的表面积 为______. 三.解答题:本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤。 17.(本小题满分 12 分)数列 ).13(2 1}{ 321 n nn aaaaa 满足: (1)求 }{ na 的通项公式; (2)若数列 .T}{,3}{ n项和的前求满足: nbab n ba nn nn 18.(本小题满分 12 分)如图,三棱锥 P ABC 中,平面 PAB 平面 ABC , PA PB ,APB ACB 90 ,点 E, F 分别是棱 AB, PB 的中点,点 G 是 △ BCE 的重心. (1)证明: GF / / 平面 PAC ; (2)若 GF 与平面 ABC 所成的角为60 ,求二面角BAPC的余弦值. 19.(本小题满分 12 分)已知点 P 到直线 y=﹣3 的距离比点 P 到点 A(0,1)的距离多 2. (1)求点 P 的轨迹方程; (2)经过点 Q(0,2)的动直线 l 与点 P 的轨迹交于 M,N 两点,是否存在定点 R 使得∠MRQ =∠NRQ?若存在,求出点 R 的坐标;若不存在,请说明理由. 20.(本小题满分 12 分)华北“一票通”景区旅游年卡,是由衡水市旅游局策划,由市某旅游公司推出 的一项惠民工程.持有旅游年卡一年内可不限次畅游华北 19 家签约景区.为了解市民每年旅游消 费支出情况(单位:百元),相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到 的数据列成如下所示的频数分布表: 4 组别 [0,20) [20,40) [40,60) [60,80) [80,100) 频数 10 390 400 188 12 (1)求所得样本的中位数(精确到百元); (2)根据样本数据,可近似地认为市民的旅游费用支出服从正态分布 245,15N .若该市总人口为 450 万人,试估计有多少市民每年旅游费用支出在 7500 元以上; (3)若年旅游消费支出在 40(百元)以上的游客一年内会继续来该景点游玩.现从游客中随机抽取 3 人,一年内继续来该景点游玩记 2 分,不来该景点游玩记 1 分.将上述调查所得的频率视为概 率,且游客之间的选择意愿相互独立.记总得分为随机变量 X,求 X 的分布列与数学期望. 附:若 2~ ,x N ,则 ( ) 0.6826p X , ( 2 2 ) 0.9544p x , ( 3 3 ) 0.9973p 21.(本小题满分 12 分)已知函数 ( ) ln xef x x x x . (1)求 ( )f x 的最大值; (2)若 1( ) ( ) 1xf x x e bxx 恒成立,求实数 b 的取值范围. 请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分.做答时,请用 2B 铅 笔在答题卡上将所选题号后的方框涂黑。 22.(本小题满分 10 分)选修 4 4:坐标系与参数方程 已知直角坐标系 xOy 中,曲线 1C 的参数方程为 3 ,x t y t (t 为参数).以O 为极点, x 轴的正 半轴为极轴,建立极坐标系,曲线 2C 的极坐标方程为 2 1 2 cos . (1)写出 1C 的普通方程和 2C 的直角坐标方程; (2)设点 P 为 2C 上的任意一点,求 P 到 1C 距离的取值范围. 23.(本小题满分 10 分)选修 4-5:不等式选讲 已知函数 2f x x m x ( m R ),不等式 2 0f x 的解集为 4, . (1)求 m 的值; (2)若 0a , 0b , 3c ,且 2 2a b c m ,求 1 1 3a b c 的最大值. 河北武邑中学 2019—2020 学年高三年级下学期期中考试 数学试题(理科)答案 5 第Ⅰ卷 选择题(共 60 分) 一.选择题:本题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,有且只有一项符 合题目要求,将正确答案填涂在答题卡上。 1.已知集合 , | 2 0A x y x y , , | 1 0B x y x my .若 A B ,则实数 m A. 2 B. 1 2 C. 1 2 D. 2 【答案】C. 【解析】因为 A B ,所以直线 2 0x y 与直线 1 0x my 平行,所以 1 2m .故选 C. 2.设复数 z 满足 1 iz z (i 为虚数单位), z 在复平面内对应的点为( x , y ),则( ) A. y x B. y x C. 2 21 1 1x y D. 2 21 1 1x y 【答案】B 【解析】设 ( , )z x yi x y R ,∵ 1 iz z ,∴ 1x yi x yi i , 即 2 2 2 2( 1) ( 1)x y x y ,化简得 y x . 故选:B. 3.已知两个单位向量 1 2,e e ,若 1 2 12 e e e ,则 1 2,e e 的夹角为 A. B. C. D. 【答案】B. 【解析】因为 1 2 12 e e e ,所以 1 2 12 0 e e e ,所以 1 1 2 22 e e e , 所以 1 2cos , e e 1 2 ,又因为 1 2, 0, e e ,所以 1 2, e e ,故选 B. 4.某学校拟从甲、乙等 5 位同学中随机选派 3 人去参加国防教育活动,则甲、乙均被选中的概率为 A. 3 5 B. 1 2 C. 2 5 D. 3 10 【答案】D 【解析】所求概率为C13 C35 = 3 10 ,故选 D. 5.已知点 ,P x y 满足不等式 3 2 0 5 0 5 0 x y x y x ,点 ,Q x y 是函数 2( ) 1f x x 的图像上任意一点, 则两点 P,Q 之间距离的最小值为( ) A. 5 2 12 B. 13 1 C.4 D. 5 2 2 【答案】A 6 【解析】如图所示,点 P 在平面区域内任一点 P,点 Q 在半圆 2 2 1(0 1)x y y 上, 过点 O 作直线的垂线,垂足为 P,交半圆于 Q,此时 PQ 取最小值, 求得 min 5 2| | 12PQ . 6.若 3 3 12 3 1log e,2 e,a b c ,则 A. a b c B. c a b C. a c b D. c b a 【答案】B. 【解析】 2 1 3 032 2 2 1a , 1 3 1 1 331 e 2e ac , 所以1 a c , 3 3log e log 3 1b ,故 c a b .故选 B. 7.若 tan 3cos( )2 ,则 cos2 A. 1 B. 7 9 C. 0 或 7 9 D. 1 或 7 9 【答案】D. 【解析】由 tan 3cos( )2 得 sin 2 3cos cos 2 ,所以 cos 3cossin , 所以 cos 0 或 sin 3 1 ,故 2cos2 2cos 1 1 或 2cos2 1 2 7 9sin .故选 D. 8. 若函数 sin 2f x x 的图象向右平移11 6 个单位得到的图象对应的函数为 g x ,则下列说法正 确的是( ) A. g x 的图象关于 12x 对称 B. g x 在 0 , 上有 2 个零点 C. g x 在区间 5 3 6 , 上单调递减 D. g x 在 02 , 上的值域为 3 02 , 7 【答案】B 【解析】由题意 11 11( ) sin 2( ) sin(2 ) sin(2 )6 3 3g x x x x , 1( ) sin( )12 6 3 2g 不是函数的最值, 12x 不是对称轴,A 错; 由 ( ) sin(2 ) 03g x x , 2 ( )3x k k Z , 2 6 kx ,其中 5,3 6 是[0, ] 上 的零点,B 正确; 由 32 2 22 3 2k x k 得 7 12 12k x k , k Z , 因此 ( )g x 在 7( , )3 12 是递减,在 7 5( , )12 6 上递增,C 错; [ ,0]2x 时, 22 [ , ]3 3 3x , 3( ) [ 1, ]2g x ,D 错. 故选:B. 9. “角谷定理”的内容为对于每一个正整数.如果它是奇数.则对它乘 3 再加 1,如果它是偶数.则对它除 以 2,如此循环,最终都能够得到 1.右图为研究角谷定理的一个程序框图.若输入 n 的值为 10.则输出 i 的值为 A.5 B.6 C.7 D.8 【答案】B 【解析】 8 10.已知椭圆 2 2 2 2 1x y a b ( 0a b )的左、右焦点分别为 1F , 2F ,点 P 为椭圆上不同于左、右 顶点的任意一点,I 为 1 2PF F 的内心,且 1 1 2 2IPF IF F IPFS S S ,若椭圆的离心率为 e,则 ( ) A. 1 e B. 2 e C.e D. 2e 【答案】A 【解析】设 1 2PF F 内切圆的半径为 r 则 1 1 1 2IPFS r PF , 2 2 1 2IPFS r PF , 1 2 1 2 1 2IF FS r F F . 1 1 2 2IPF IF F IPFS S S , 1 1 2 2 1 1 2 2 2r PF r F F r PF 整理得 1 2 1 2F F PF PF ,∵P 为椭圆上的点, 2 2c a ,解得 1 e . 故选:A 11.已知双曲线 2 2 2 2: 1( 0, 0)x yC a ba b 的一条渐近线方程为 2 0x y , ,A B 是C 上关于原点对称 的两点, M 是 C 上异于 ,A B 的动点,直线 ,MA MB 的斜率分别为 1 2,k k ,若 11 2k ,则 2k 的取 值范围为 A. 1 1,8 4 B. 1 1,4 2 C. 1 1,4 8 D. 1 1,2 4 【答案】A. 【解析】∵双曲线 2 2 2 2: 1( 0, 0)x yC a ba b 的一条渐近线方程为 2 0x y ,∴ 2a b , 则双曲线的方程为: 2 2 2 2 1( 0)4 x y bb b , 9 设 1 1,A x y , 0 0,M x y ,则 1 1,B x y ,所以 2 2 1 1 2 2 2 2 0 0 2 2 1 4 , 1 4 x y b b x y b b 1 0 1 0 1 0 1 0 1 0 1 0 2 2 1 0 1 0 1, 44 x x x x y y y y y y y y x x x xb b , 即 1 2 1 4k k ,∵ 11 2k ,∴ 2 1 1,8 4k .故选 A. 12.若函数 ln xf x a x e 有极值点,则实数 a 的取值范围是 A. ,e B. 1,e C. 1, D. 0, 【答案】D 【解析】 第Ⅱ卷 非选择题(共 90 分) 二.填空题:本大题共 4 小题,每小题 5 分,共 20 分,将答案填在答题卡上相应位置。 13.已知函数 f(x)=ae x +x+b,若函数 f(x)在(0,f(0))处的切线方程为 y=2x+3,则 ab 的值为______. 【答案】2 【解析】 14. 41(1 )(1 2 )xx 展开式中 x 2 的系数为______. 【答案】56 【解析】 10 15.勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先 发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三 段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的 边长比为1:3 ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛 三角形内的概率为______. 【答案】 1 9 . 【解析】设图中的小的勒洛三角形所对应的等边三角形的边长为 a ,则小 勒洛三角形的面积为 2 1 2 2 3 2 3 46 2a aaS ,因为大 小两个勒洛三角形,它们所对应的等边三角形的边长比为1:3 ,所以大勒洛三角形的面积 为 2 2 2 2 3 9 2 a a S ,若从大的勒洛三角形中随机取一点,则此点取自小 勒洛三角形内的概率为 1 2 1 9 S SP . 16.平行四边形 ABCD 中, ABD 是腰长为 2 的等腰直角三角形, 90ABD ,现将 ABD 沿 BD 折起,使二面角 A BD C 大小为 2 3 ,若 A,B,C,D 四点在同一球面上,则该球的表面积 为______. 【答案】 20 【解析】由题意,取 AD , BC 的中点分别为 1O , 2O , 过 1O 作面 ABD 的垂线与过 2O 作面 BCD 的垂线, 两垂线交点 O 即为所求外接球的球心, 取 BD中点 E,连结 1O E , 2O E , 则 1 2O EO 即为二面角 A BD C 的平面角, 又由 1 2 1O E O E ,连接OE , 在 1Rt O OE 中,则 1 3O O ,在 1Rt O OA 中, 1 2O A ,得 5OA , 即球半径为 5R OA ,所以球面积为 24 20S R 11 . 三.解答题:本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤。 17.(本小题满分 12 分)数列 ).13(2 1}{ 321 n nn aaaaa 满足: (1)求 }{ na 的通项公式; (2)若数列 .T}{,3}{ n项和的前求满足: nbab n ba nn nn 【解】 6 分 ………………………7 分 9 分 ………………………10 分 ………………………12 分 18.(本小题满分 12 分)如图,三棱锥 P ABC 中,平面 PAB 平面 ABC , PA PB ,APB ACB 90 ,点 E, F 分别是棱 AB, PB 的中点,点 G 是 △ BCE 的重心. (1)证明: GF / / 平面 PAC ; (2)若 GF 与平面 ABC 所成的角为60 ,求二面角BAPC的余弦值. 12 【解】 13 19.(本小题满分 12 分)已知点 P 到直线 y=﹣3 的距离比点 P 到点 A(0,1)的距离多 2. (1)求点 P 的轨迹方程; (2)经过点 Q(0,2)的动直线 l 与点 P 的轨迹交于 M,N 两点,是否存在定点 R 使得∠MRQ =∠NRQ?若存在,求出点 R 的坐标;若不存在,请说明理由. 【解】(1)根据题意,|PA|的距离与 P 到直线 y=﹣1 的距离相等, 故 P 的轨迹为以 A 为焦点,y=﹣1 为准线的抛物线, 所以方程为 x2=4y; (2)根据抛物线的对称性知,若点存在一定在 y 轴上,设 R(0,r), 由∠MRQ=∠NRQ 得 kNQ+kMQ=0, 设 M(x1,y1),N(x2,y2),则 , 由题意显然 l 的斜率存在,设 l 为:y=kx+2, 由 ,得 x2﹣4kx﹣8=0, 得 x1+x2=4k,x1x2=﹣8, 由 2k 2k , 故 r=﹣2, 所以存在定点 R(0,﹣2). 20.(本小题满分 12 分)华北“一票通”景区旅游年卡,是由衡水市旅游局策划,由市某旅游公司推出 的一项惠民工程.持有旅游年卡一年内可不限次畅游华北 19 家签约景区.为了解市民每年旅游消 费支出情况(单位:百元),相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到 的数据列成如下所示的频数分布表: 组别 [0,20) [20,40) [40,60) [60,80) [80,100) 频数 10 390 400 188 12 (1)求所得样本的中位数(精确到百元); (2)根据样本数据,可近似地认为市民的旅游费用支出服从正态分布 245,15N .若该市总人口为 450 万人,试估计有多少市民每年旅游费用支出在 7500 元以上; (3)若年旅游消费支出在 40(百元)以上的游客一年内会继续来该景点游玩.现从游客中随机抽取 3 人,一年内继续来该景点游玩记 2 分,不来该景点游玩记 1 分.将上述调查所得的频率视为概 率,且游客之间的选择意愿相互独立.记总得分为随机变量 X,求 X 的分布列与数学期望. 附:若 2~ ,x N ,则 ( ) 0.6826p X , ( 2 2 ) 0.9544p x , ( 3 3 ) 0.9973p 14 【解】(1)设样本的中位数为 x,则 4010 390 400 0.51000 1000 1000 20 x , 解得 45x= ,所得样本中位数为(百元).…………2 分 (2) 45 , 15 , 2 75 , 旅游费用支出在 7500 元以上的概率为 2P x 1 ( 2 2 ) 1 0.9544 0.02282 2 P x , 0.0228 450 10.26 , 估计有 10.26 万市民旅游费用支出在 7500 元以上.…………6 分 (3)由表格知一年内游客继续来该景点游玩的概率为 3 5 ,X 可能取值为 3,4,5,6 32 83 5 125P X , 2 1 3 3 2 364 5 5 125P X C , 2 2 3 3 2 545 5 5 125P X C , 33 276 5 125P X , 故其分布列为 X 3 4 5 6 P 8 125 36 125 54 125 27 125 8 36 54 27 243 4 5 6125 125 125 125 5E X .………12 分 21.(本小题满分 12 分)已知函数 ( ) ln xef x x x x . (1)求 ( )f x 的最大值; (2)若 1( ) ( ) 1xf x x e bxx 恒成立,求实数 b 的取值范围. 【解】(1) ( ) ln xef x x x x ,定义域 (0, ) , 2 2 1 ( 1) ( 1)( )( ) 1 x xe x x x ef x x x x , 由 1xe x x , ( )f x 在 (0,1]增,在 (1, ) 减, max( ) (1) 1f x f e (2) 1( ) ( )e 1xf x x bxx e eln e 1 x x xx x x bxx x ln e 1 0xx x x bx e ln 1xx x x bx 15 min e ln 1( ) , xx x x bx 令 e ln 1( ) xx x xx x , 2 ln( ) xx e xx x 令 2( ) lnxh x x e x , ( )h x 在 (0, ) 单调递增, 0, ( )x h x , (1) 0h e ( )h x 在 (0,1) 存在零点 0x , 即 02 0 0 0( ) ln 0xh x x e x 0 0 0 1ln 2 0 0 0 0 0 0 ln 1ln 0 (ln )( )x x xxx e x x e ex x , 由于 xy xe 在 (0, ) 单调递增,故 0 0 0 1ln ln ,x xx 即 0 0 1xe x ( )x 在 0(0, )x 减,在 0( , )x 增, 0 0 0 0 0 0 min 0 0 e ln 1 1 1( ) 2 xx x x x xx x x 所以 2b . 请考生在 22、23 题中任选一题作答,如果多做,则按所做的第一题计分.做答时,请用 2B 铅 笔在答题卡上将所选题号后的方框涂黑。 22.(本小题满分 10 分)选修 4 4:坐标系与参数方程 已知直角坐标系 xOy 中,曲线 1C 的参数方程为 3 ,x t y t (t 为参数).以O 为极点, x 轴的正 半轴为极轴,建立极坐标系,曲线 2C 的极坐标方程为 2 1 2 cos . (1)写出 1C 的普通方程和 2C 的直角坐标方程; (2)设点 P 为 2C 上的任意一点,求 P 到 1C 距离的取值范围. 【解】(1) 1C 的普通方程为 3x y ,即 3 0x y .·································2 分 2C 的直角坐标方程为 2 2 1 2x y x ,即 2 21 2x y .···············5 分 (2)由(1)知, 2C 是以 1,0 为圆心,半径 2r 的圆, 圆心 2C 1,0 到 1C 的距离 1 0 3 2 2 2 2 d > ,························7 分 所以直线 1C 与圆 2C 相离, P 到 1C 距离的最小值为 2 2 2 2d r ;····························· 8 分 最大值为 2 2d r 2 3 2 ,·····························9 分 所以 P 到 1C 距离的取值范围为 2,3 2 .·································· 10 分 23.(本小题满分 10 分)选修 4-5:不等式选讲 16 已知函数 2f x x m x ( m R ),不等式 2 0f x 的解集为 4, . (1)求 m 的值; (2)若 0a , 0b , 3c ,且 2 2a b c m ,求 1 1 3a b c 的最大值. 【解】(1)∵ 2f x x m x , 2 2 2 2f x x m x , 所以不等式 2 0f x 的解集为 4, , 即为不等式 2 0x m x 的解集为 4, , ∴ 2x m x 的解集为 4, , 即不等式 2 22x m x 的解集为 4, , 化简可得,不等式 2 2 2 0m m x 的解集为 4, , 所以 2 42 m ,即 6m . (2)∵ 6m ,∴ 2 12a b c . 又∵ 0a , 0b , 3c , ∴ 1 2 2 31 1 3 2 a b ca b c 3 3 31 2 2 31 1 2 1 12 322 3 2 3 2 3 a b c a b c , 当且仅当 1 2 2 3a b c , 2 12a b c 等号成立, 即 3a , 1b , 7c 时,等号成立, ∴ 1 1 3a b c 的最大值为 32.查看更多