【数学】2020届一轮复习(文理合用)第9章算法初步、统计、统计案例作业
对应学生用书[考案9理][考案9文]
第九章 综合过关规范限时检测
(时间:120分钟 满分150分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)
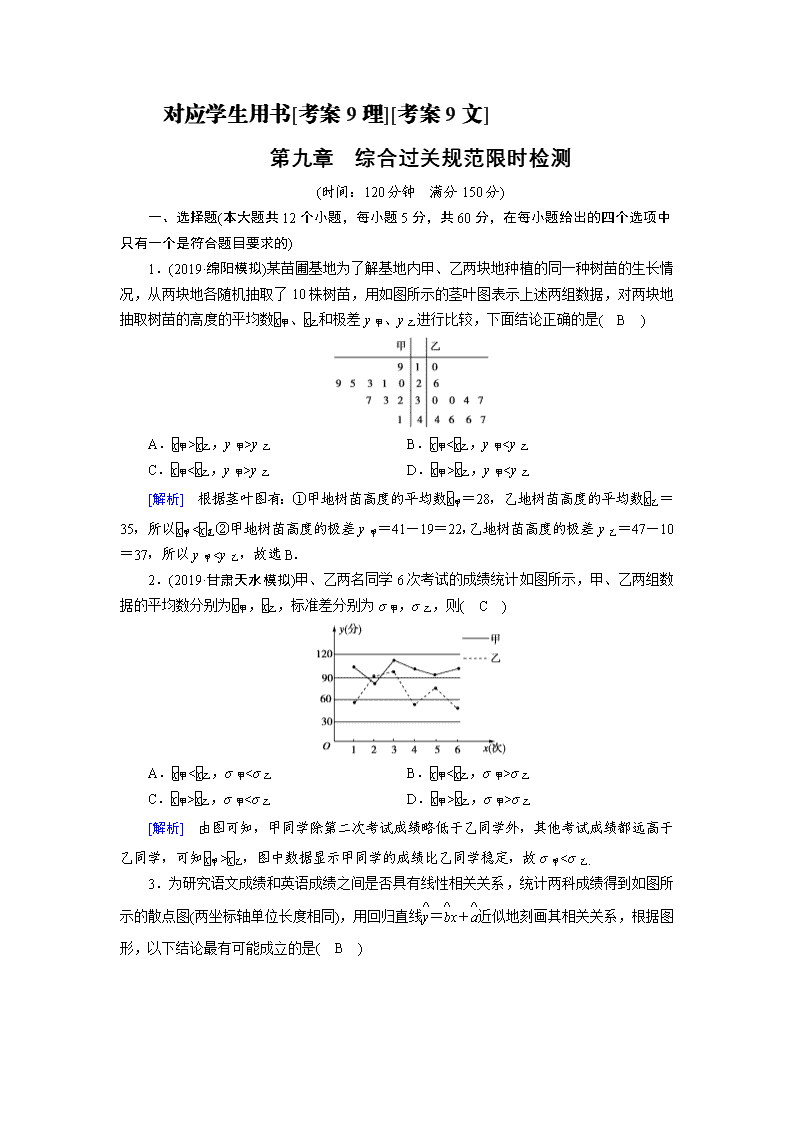
1.(2019·绵阳模拟)某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的生长情况,从两块地各随机抽取了10株树苗,用如图所示的茎叶图表示上述两组数据,对两块地抽取树苗的高度的平均数甲、乙和极差y甲、y乙进行比较,下面结论正确的是( B )
A.甲>乙,y甲>y乙 B.甲<乙,y甲
y乙 D.甲>乙,y甲σ乙
C.甲>乙,σ甲<σ乙 D.甲>乙,σ甲>σ乙
[解析] 由图可知,甲同学除第二次考试成绩略低于乙同学外,其他考试成绩都远高于乙同学,可知甲>乙,图中数据显示甲同学的成绩比乙同学稳定,故σ甲<σ乙.
3.为研究语文成绩和英语成绩之间是否具有线性相关关系,统计两科成绩得到如图所示的散点图(两坐标轴单位长度相同),用回归直线=x+近似地刻画其相关关系,根据图形,以下结论最有可能成立的是( B )
A.线性相关关系较强,的值为1.25
B.线性相关关系较强,的值为0.83
C.线性相关关系较强,的值为-0.87
D.线性相关关系太弱,无研究价值
[解析] 由散点图可知,点的分布比较集中,在一条直线附近,所以语文成绩和英语成绩之间具有线性相关关系,且线性相关关系较强,由于所有的点都在直线y=x的下方,所以回归直线的斜率小于1,故结论最有可能成立的是B.
4.某校共有高一、高二、 高三学生1290人,其中高一480人,高二比高三多30人,为了解该校学生的健康状况,现采用分层抽样的方法进行抽样调查,在抽取的样本中有高一学生96人,则该样本中高三学生的人数为( B )
A.84 B.78
C.81 D.96
[解析] 设该校高三有x人,则高二有(30+x)人,故480+x+(30+x)=1290,∴x=390,设样本中高三学生人数为t,则=,∴t=78.
5.(2019·辽宁抚顺模拟)如图所示的是某校高二(2)班50名学生某次数学测试成绩的频率分布折线图,根据图中所提供的信息,下列结论正确的是( D )
A.成绩为50分或100分的人数是0
B.成绩为75分的人数是20
C.成绩为60分的频率是0.18
D.成绩落在60~80分的人数是29
[解析] 频率分布折线图表示的是某一个范围的频率,故A,B,C选项是错误的,对于D选项,成绩落在60~80分的人数为50×(0.018+0.04)×10=29,故选D.
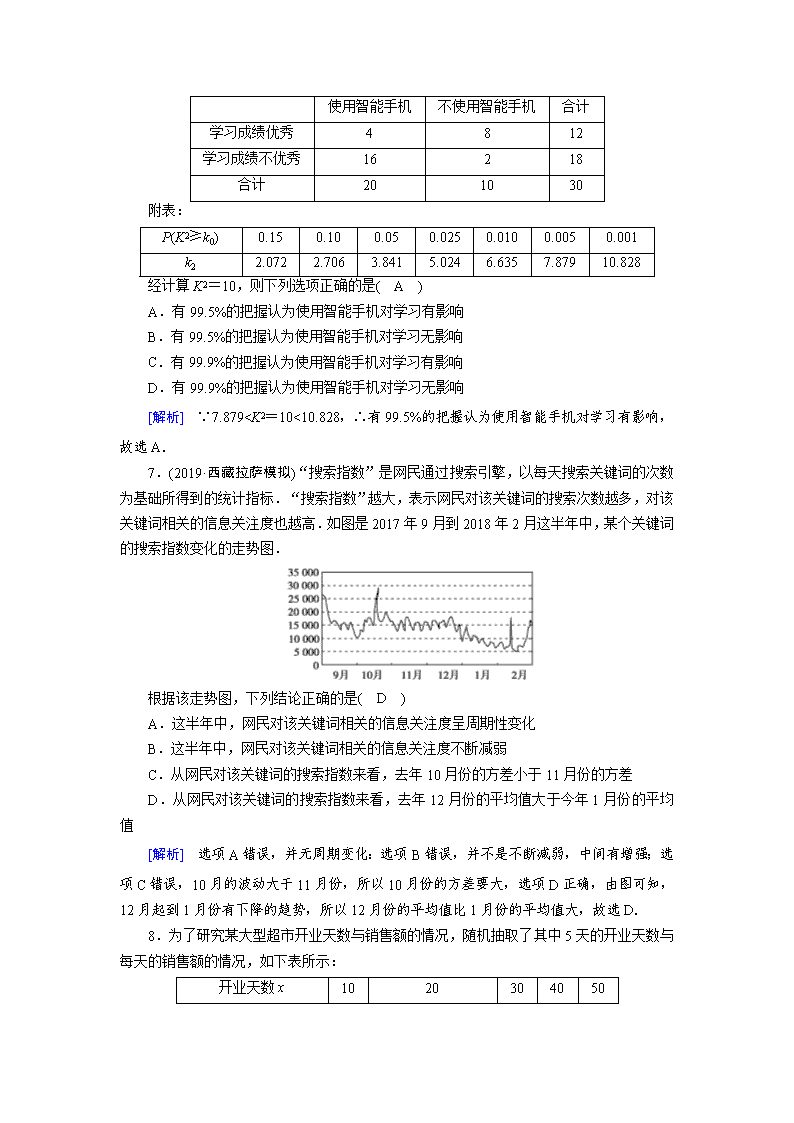
6.(2019·黑龙江佳木斯模拟)某研究型学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如下表:
使用智能手机
不使用智能手机
合计
学习成绩优秀
4
8
12
学习成绩不优秀
16
2
18
合计
20
10
30
附表:
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k2
2.072
2.706
3.841
5.024
6.635
7.879
10.828
经计算K2=10,则下列选项正确的是( A )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响
[解析] ∵7.8796.635,
故有99%的把握认为物理成绩好与否和数学成绩有关.
21.(本题满分15分)(2019·北京模拟)第23届冬季奥林匹克运动会于2018年2月9日~25日在韩国平昌郡举行,简称“平昌冬奥会”.某媒体随机采访了某市20名关心“平昌冬奥会”的市民,其年龄数据可绘制成如图所示的茎叶图,由于其中部分数据缺失,故打算根据频率分布直方图中的数据估计被采访的市民的平均年龄.
(1)完成频率分布直方图;
(2)根据(1)中的频率分布直方图估计被采访的市民的平均年龄x(同一组中的数据用该组区间的中点值作代表);
(3)根据茎叶图计算出被采访的市民的平均年龄为y,并假设a∈{n∈Z|0≤n≤9},且a取得每一个可能值的机会相等,在(2)的条件下,求P(y>x).
[解析] (1)频率分布直方图如图:
(2)x=25×0.1+35×0.15+45×0.3+55×0.25+65×0.2=48,即估计被采访的市民的平均年龄为48岁.
(3)y==,
故P(y>x)=P(>48)=P(a>2)=0.7.
22.(本题满分15分)(2019·河南洛阳)某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东、西部各5个城市,得到观看该节目的人数的统计数据(单位:千人),并画出如下茎叶图,其中一个数字被污损.
(1)求东部各城市观看该节目的观众的平均人数超过西部各城市观看该节目的观众的平均人数的概率;
(2)该节目的播出极大地激发了观众对成语知识学习积累的热情,现从观看节目的观众中随机统计了4位观众学习成语知识的周均时间(单位:小时)与年龄(单位:岁),并制作了如下对照表:
年龄x
20
30
40
50
周均学习成语知识时间y
2.5
3
4
4.5
根据表中数据,试求线性回归方程=x+,并预测年龄为50岁的观众周均学习成语知识的时间.
参考公式:=,=-.
[解析] (1)设被污损的数字为a,则a有10种情况.
由88+89+90+91+92>83+83+87+90+a+99,得a<8,
∴有8种情况使得东部各城市观看该节目的观众的平均人数超过西部各城市观看该节目的观众的平均人数,
所求概率为=.
(2)由表中数据,计算得=35,=3.5,===,
=-=3.5-×35=.
∴=x+.
当x=50时,=4.55.
即预测年龄为50岁的观众周均学习成语知识的时间为4.55小时.