高中数学（人教版a版必修一）配套单元检测：第三章函数的应用章末检测aword版含解析

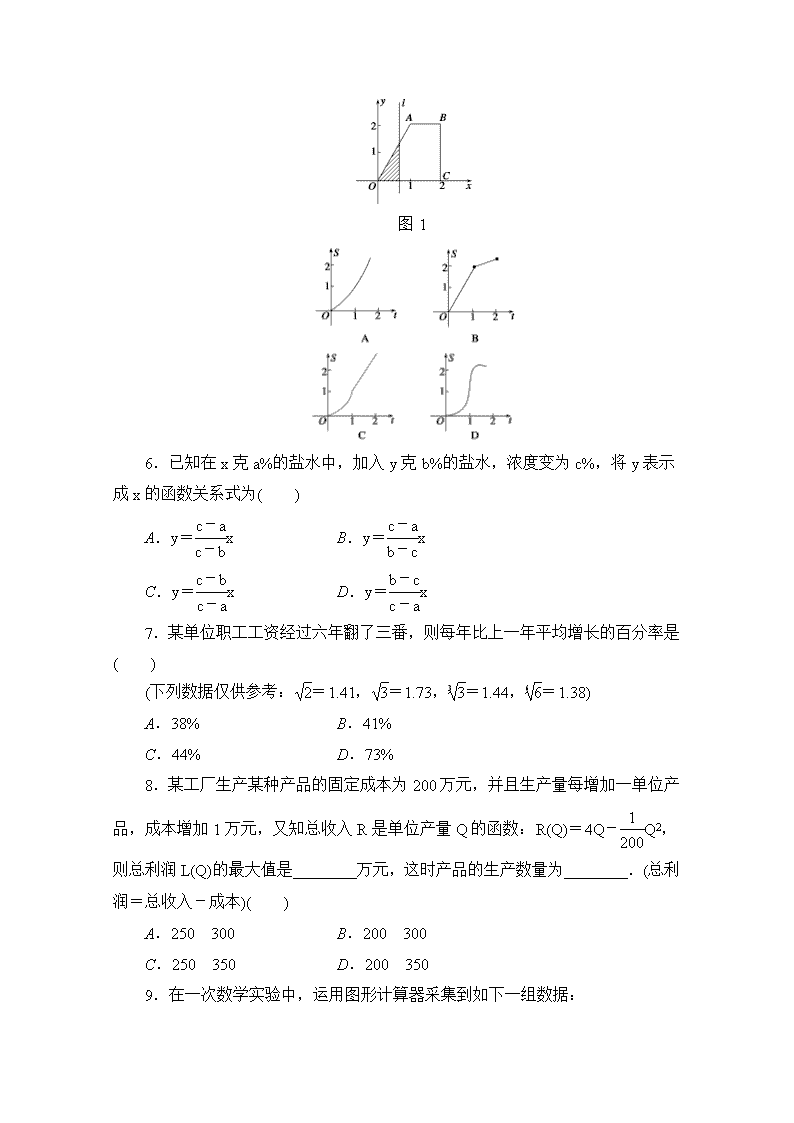
高中数学（人教版a版必修一）配套单元检测：第三章函数的应用章末检测aword版含解析

章末检测(A) (时间：120 分钟 满分：150 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分) 1．函数 y＝1＋1 x 的零点是( ) A．(－1,0) B．－1 C．1 D．0 2．设函数 y＝x3 与 y＝(1 2)x－2 的图象的交点为(x0，y0)，则 x0 所在的区间是( ) A．(0,1) B．(1,2) C．(2,3) D．(3,4) 3．某企业 2010 年 12 月份的产值是这年 1 月份产值的 P 倍，则该企业 2010 年度产值的月平均增长率为( ) A. P P－1 B.11 P－1 C.11 P D.P－1 11 4．如图所示的函数图象与 x 轴均有交点，其中不能用二分法求图中交点横坐 标的是( ) A．①③ B．②④ C．①② D．③④ 5．如图 1，直角梯形 OABC 中，AB∥OC，AB＝1，OC＝BC＝2，直线 l∶x ＝t 截此梯形所得位于 l 左方图形面积为 S，则函数 S＝f(t)的图象大致为图中的 ( ) 图 1 6．已知在 x 克 a%的盐水中，加入 y 克 b%的盐水，浓度变为 c%，将 y 表示 成 x 的函数关系式为( ) A．y＝c－a c－b x B．y＝c－a b－c x C．y＝c－b c－a x D．y＝b－c c－a x 7．某单位职工工资经过六年翻了三番，则每年比上一年平均增长的百分率是 ( ) (下列数据仅供参考： 2＝1.41， 3＝1.73，3 3＝1.44，6 6＝1.38) A．38% B．41% C．44% D．73% 8．某工厂生产某种产品的固定成本为 200 万元，并且生产量每增加一单位产 品，成本增加 1 万元，又知总收入 R 是单位产量 Q 的函数：R(Q)＝4Q－ 1 200Q2， 则总利润 L(Q)的最大值是________万元，这时产品的生产数量为________．(总利 润＝总收入－成本)( ) A．250 300 B．200 300 C．250 350 D．200 350 9．在一次数学实验中，运用图形计算器采集到如下一组数据： x －2.0 －1.0 0 1.00 2.00 3.00 y 0.24 0.51 1 2.02 3.98 8.02 则 x、y 的函数关系与下列哪类函数最接近？(其中 a、b 为待定系数)( ) A．y＝a＋bx B．y＝a＋bx C．y＝ax2＋b D．y＝a＋b x 10．根据统计资料，我国能源生产自 1986 年以来发展得很快，下面是我国能 源生产总量(折合亿吨标准煤)的几个统计数据：1986 年 8.6 亿吨，5 年后的 1991 年 10.4 亿吨，10 年后的 1996 年 12.9 亿吨，有关专家预测，到 2001 年我国能源生 产总量将达到 16.1 亿吨，则专家是以哪种类型的函数模型进行预测的？( ) A．一次函数 B．二次函数 C．指数函数 D．对数函数 11．用二分法判断方程 2x3＋3x－3＝0 在区间(0,1)内的根(精确度 0.25)可以是 (参考数据：0.753＝0.421875,0.6253＝0.24414)( ) A．0.25 B．0.375 C．0.635 D．0.825 12．有浓度为 90%的溶液 100g，从中倒出 10g 后再倒入 10g 水称为一次操作， 要使浓度低于 10%，这种操作至少应进行的次数为(参考数据：lg2＝0.3010，lg3 ＝0.4771)( ) A．19 B．20 C．21 D．22 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分) 13．用二分法研究函数 f(x)＝x3＋2x－1 的零点，第一次经计算 f(0)<0，f(0.5)>0， 可得其中一个零点 x0∈________，第二次计算的 f(x)的值为 f(________)． 14．若函数 f(x)＝ax－x－a(a>0，且 a≠1)有两个零点，则实数 a 的取值范围为 ________． 15．一批设备价值 a 万元，由于使用磨损，每年比上一年价值降低 b%，则 n 年后这批设备的价值为________________万元． 16．函数 f(x)＝x2－2x＋b 的零点均是正数，则实数 b 的取值范围是________． 三、解答题(本大题共 6 小题，共 70 分) 17．(10分)华侨公园停车场预计“十·一”国庆节这天停放大小汽车1200 辆次， 该停车场的收费标准为：大车每辆次 10 元，小车每辆次 5 元． (1)写出国庆这天停车场的收费金额 y(元)与小车停放辆次 x(辆)之间的函数关 系式，并指出 x 的取值范围． (2)如果国庆这天停放的小车占停车总辆数的 65%～85%，请你估计国庆这天 该停车场收费金额的范围． 18．(12 分)光线通过一块玻璃，其强度要损失 10%，把几块这样的玻璃重叠 起来，设光线原来的强度为 a，通过 x 块玻璃后强度为 y. (1)写出 y 关于 x 的函数关系式； (2)通过多少块玻璃后，光线强度减弱到原来的1 3 以下？(lg3≈0.4771) 19．(12 分)某医药研究所开发一种新药，据监测，如果成人按规定的剂量服用， 服用药后每毫升中的含药量 y(微克)与服药的时间 t(小时)之间近似满足如图所示的 曲线，其中 OA 是线段，曲线 AB 是函数 y＝kat(t≥1，a>0，且 k，a 是常数)的图 象． (1)写出服药后 y 关于 t 的函数关系式； (2)据测定，每毫升血液中的含药量不少于 2 微克时治疗疾病有效．假设某人 第一次服药为早上 6∶00，为保持疗效，第二次服药最迟应当在当天几点钟？ (3)若按(2)中的最迟时间服用第二次药，则第二次服药后 3 小时，该病人每毫 升血液中的含药量为多少微克(精确到 0.1 微克)? 20．(12 分)已知一次函数 f(x)满足：f(1)＝2，f(2)＝3， (1)求 f(x)的解析式； (2)判断函数 g(x)＝－1＋lgf2(x)在区间[0,9]上零点的个数． 21．(12 分)截止到 2009 年底，我国人口约为 13.56 亿，若今后能将人口平均 增长率控制在 1%，经过 x 年后，我国人口为 y 亿． (1)求 y 与 x 的函数关系式 y＝f(x)； (2)求函数 y＝f(x)的定义域； (3)判断函数 f(x)是增函数还是减函数？并指出函数增减的实际意义． 22．(12 分)某厂生产某种零件，每个零件的成本为 40 元，出厂单价定为 60 元．该厂为鼓励销售商订购，决定当一次订购量超过 100 个时，每多订购一个， 订购的全部零件的出厂单价就降低 0.02 元，但实际出厂单价不能低于 51 元． (1)当一次订购量为多少个时，零件的实际出厂单价恰降为 51 元？ (2)设一次订购量为 x 个，零件的实际出厂单价为 P 元，写出函数的表达式； (3)当销售商一次订购 500 个零件时，该厂获得的利润是多少元？如果订购 1000 个，利润又是多少元？(工厂售出一个零件的利润＝实际出厂单价－成本) 章末检测(A) 1．B [由 1＋1 x ＝0，得1 x ＝－1，∴x＝－1.] 2．B [由题意 x0 为方程 x3＝(1 2)x－2 的根， 令 f(x)＝x3－22－x， ∵f(0)＝－4<0，f(1)＝－1<0，f(2)＝7>0， ∴x0∈(1,2)．] 3．B [设 1 月份产值为 a，增长率为 x，则 aP＝a(1＋x)11， ∴x＝11 P－1.] 4．A [对于①③在函数零点两侧函数值的符号相同，故不能用二分法求．] 5．C [解析式为 S＝f(t) ＝ 1 2t·2t 0≤t≤1 1 2 ×1×2＋t－1×210，f(0.5)<0，f(0.75)>0，f(0.625)<0， ∴方程 2x3＋3x－3＝0 的根在区间(0.625,0.75)内， ∵0.75－0.625＝0.125<0.25， ∴区间(0.625,0.75)内的任意一个值作为方程的近似根都满足题意．] 12．C [操作次数为 n 时的浓度为( 9 10)n＋1，由( 9 10)n＋1<10%，得 n＋1> －1 lg 9 10 ＝ －1 2lg3－1 ≈21.8， ∴n≥21.] 13．(0,0.5) 0.25 解析 根据函数零点的存在性定理． ∵f(0)<0，f(0.5)>0， ∴在(0,0.5)存在一个零点，第二次计算找中点， 即0＋0.5 2 ＝0.25. 14．(1，＋∞) 解析 函数 f(x)的零点的个数就是函数 y＝ax 与函数 y＝x＋a 交点的个数，如 下图，由函数的图象可知 a>1 时两函数图象有两个交点，01. 15．a(1－b%)n 解析 第一年后这批设备的价值为 a(1－b%)； 第二年后这批设备的价值为 a(1－b%)－a(1－b%)·b%＝a(1－b%)2； 故第 n 年后这批设备的价值为 a(1－b%)n. 16．(0,1] 解析 设 x1，x2 是函数 f(x)的零点，则 x1，x2 为方程 x2－2x＋b＝0 的两正根， 则有 Δ≥0 x1＋x2＝2>0 x1x2＝b>0 ，即 4－4b≥0 b>0 . 解得 00， ∴函数 g(x)在区间[0,9]上零点的个数为 1 个． 21．解 (1)2009 年底人口数：13.56 亿． 经过 1 年，2010 年底人口数： 13．56＋13.56×1%＝13.56×(1＋1%)(亿)． 经过 2 年，2011 年底人口数： 13．56×(1＋1%)＋13.56×(1＋1%)×1% ＝13.56×(1＋1%)2(亿)． 经过 3 年，2012 年底人口数： 13．56×(1＋1%)2＋13.56×(1＋1%)2×1% ＝13.56×(1＋1%)3(亿)． ∴经过的年数与(1＋1%)的指数相同． ∴经过 x 年后人口数为 13.56×(1＋1%)x(亿)． ∴y＝f(x)＝13.56×(1＋1%)x. (2)理论上指数函数定义域为 R. ∵此问题以年作为时间单位． ∴此函数的定义域是{x|x∈N*}． (3)y＝f(x)＝13.56×(1＋1%)x. ∵1＋1%>1,13.56>0， ∴y＝f(x)＝13.56×(1＋1%)x 是增函数， 即只要递增率为正数，随着时间的推移，人口的总数总在增长． 22．解 (1)设每个零件的实际出厂价恰好降为 51 元时，一次订购量为 x0 个， 则 x0＝100＋60－51 0.02 ＝550. 因此，当一次订购量为 550 个时，每个零件的实际出厂价恰好降为 51 元． (2)当 0

查看更多