【数学】2019届一轮复习北师大版程序框图学案

【数学】2019届一轮复习北师大版程序框图学案

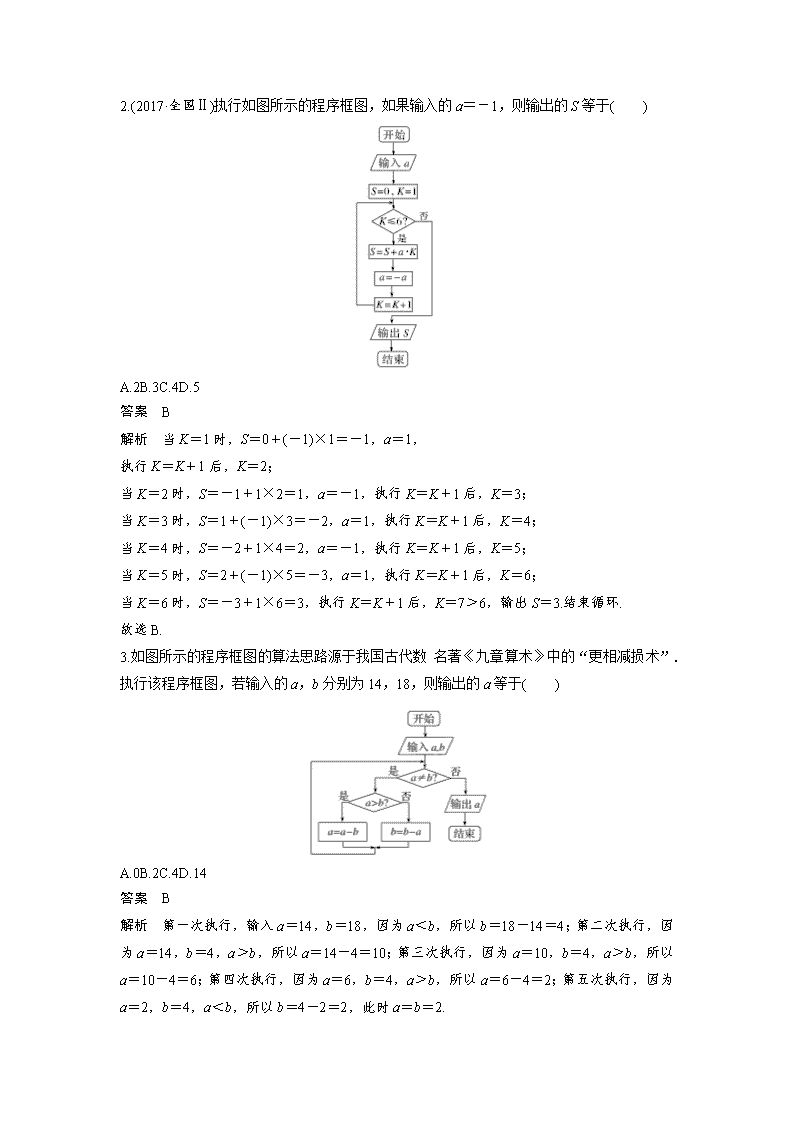
第17练　程序框图 ‎[明考情]‎ 程序框图是每年必考题，一般以选择题形式呈现，中低档难度；近几年有和其他知识或传统文化相结合的题目出现.‎ ‎[知考向]‎ ‎1.程序框图的输出.‎ ‎2.程序框图的填充.‎ ‎3.程序框图的综合应用.‎ 考点一　程序框图的输出 方法技巧　程序框图中循环结构是高考考查的重点，确定循环结构的输出结果要注意以下几点：‎ ‎(1)明确循环次数和循环条件，把握循环变量的变化情况.‎ ‎(2)模拟运行循环变量取初始值和最后几个值时输出结果的变化.‎ ‎1.阅读如图所示的程序框图，若运行相应的程序，则输出的S的值是(　　)‎ A.39 B.21‎ C.81 D.102‎ 答案　D 解析　第一次循环，S＝3，n＝2；‎ 第二次循环，S＝3＋2×32＝21，n＝3；‎ 第三次循环，S＝21＋3×33＝102，n＝4；‎ 第四次循环，不满足条件，输出S＝102.‎ ‎2.(2017·全国Ⅱ)执行如图所示的程序框图，如果输入的a＝－1，则输出的S等于(　　)‎ A.2B.3C.4D.5‎ 答案　B 解析　当K＝1时，S＝0＋(－1)×1＝－1，a＝1，‎ 执行K＝K＋1后，K＝2；‎ 当K＝2时，S＝－1＋1×2＝1，a＝－1，执行K＝K＋1后，K＝3；‎ 当K＝3时，S＝1＋(－1)×3＝－2，a＝1，执行K＝K＋1后，K＝4；‎ 当K＝4时，S＝－2＋1×4＝2，a＝－1，执行K＝K＋1后，K＝5；‎ 当K＝5时，S＝2＋(－1)×5＝－3，a＝1，执行K＝K＋1后，K＝6；‎ 当K＝6时，S＝－3＋1×6＝3，执行K＝K＋1后，K＝7＞6，输出S＝3.结束循环.‎ 故选B.‎ ‎3.如图所示的程序框图的算法思路源于我国古代数 名著《九章算术》中的“更相减损术”.执行该程序框图，若输入的a，b分别为14，18，则输出的a等于(　　)‎ A.0B.2C.4D.14‎ 答案　B 解析　第一次执行，输入a＝14，b＝18，因为a＜b，所以b＝18－14＝4；第二次执行，因为a＝14，b＝4，a＞b，所以a＝14－4＝10；第三次执行，因为a＝10，b＝4，a＞b，所以a＝10－4＝6；第四次执行，因为a＝6，b＝4，a＞b，所以a＝6－4＝2；第五次执行，因为a＝2，b＝4，a＜b，所以b＝4－2＝2，此时a＝b＝2.‎ ‎4.执行如图所示的程序框图，如果输入的t∈[－1，3]，则输出的s的取值范围为______.‎ 答案　[－3，4]‎ 解析　本程序的条件结果对应的表达式为s＝ 则当t∈[－1，1)时，s＝3t∈[－3，3)；‎ 当t∈[1，3]时，s＝4t－t2＝－(t－2)2＋4∈[3，4].‎ 综上，s∈[－3，4].‎ ‎5.公元263年左右，我国数 家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”，利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为________.(参考数据：sin15°＝0.2588，sin7.5°＝0.1305)‎ 答案　24‎ 解析　初始条件n＝6，运行第一次，S＝×6×＜3.10；运行第二次，n＝12，S＝×12×sin30°＝3＜3.10；运行第三次，n＝24，S＝×24×sin15°＝12×0.2588＝3.1056＞3.10.满足条件，停止运行，所以输出的n＝24.‎ 考点二　程序框图的填充 方法技巧　(1)条件结构的程序框图可结合分段函数的思想根据输出结果确定填充内容.‎ ‎(2)循环结构的程序框图可先假设i＞n或i＜n，模拟运行，直到运行结果和题目要求一致.‎ ‎6.如图所示的程序框图能判断任意输入的数x的奇偶性，其中判断框内的条件是(　　)‎ A.m＝0? B.m＝1?‎ C.x＝0? D.x＝1?‎ 答案　B 解析　由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以2的余数是1还是0.‎ 由图可知应该填m＝1？.‎ ‎7.执行如图所示的程序框图，若输出的S的值为2，则判断框中填入的条件可以是(　　)‎ A.n<98? B.n<99?‎ C.n<100? D.n≤100?‎ 答案　B 解析　依次执行程序框图，得S＝0，n＝1；S＝lg2，n＝2；‎ S＝lg2＋lg3－lg2＝lg3，n＝3；S＝lg3＋lg4－lg3＝lg4，n＝4；…；S＝lg99，n＝99；S＝lg100＝2，满足题设条件，必须退出循环，此时判断框中应填入n<99？，故选B.‎ ‎8.执行如图所示的程序框图，若输出的结果为，则判断框中应填入的条件是(　　)‎ A.k＞5? B.k＞6?‎ C.k＞7? D.k＞8?‎ 答案　B 解析　第一次运行S＝1＋，k＝2；第二次运行S＝1＋＋，k＝3；…；第n次运行S＝1＋＋＋…＋＝，k＝n＋1，此时结束循环，得n＝6，故判断框中应该填入“k＞6？”.‎ ‎9.执行如图所示的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中应填入(　　)‎ A.c＞x? B.x＞c?‎ C.c＞b? D.b＞c?‎ 答案　A 解析　由于要取a，b，c中的最大数，输出的x应当是a，b，c中的最大者，所以应填比较x与c大小的语句，结合各选项知选A.‎ ‎10.(2017·原创押题预测卷)如图所示的程序框图中，若输入互不相等的三个正实数a，b，‎ c(abc≠0)，要求判断△ABC的形状，则空白的判断框应填入(　　)‎ A.a2＋b2>c2? B.a2＋c2>b2?‎ C.b2＋c2>a2? D.b2＋a2＝c2?‎ 答案　C 解析　由程序框图可知，框图中前两个判断框为选出a，b，c中最长边a，可知当输出“锐角三角形”时，需满足b2＋c2>a2，故选C.‎ 考点三　程序框图的综合应用 方法技巧　程序框图往往借助其他数 问题实现，常与函数求值、数列求和、统计量计算、不等式求解相结合，解决这类问题的关键是准确理解程序框图的实际意义，把握算法运行的规律.‎ ‎11.根据如图所示程序框图，对大于2的整数N，输出的数列的通项公式是(　　)‎ A.an＝2n B.an＝2(n－1)‎ C.an＝2n D.an＝2n－1‎ 答案　C 解析　因为N＞2，所以可取N＝3，则a1＝2×1＝2，S＝a1＝2，i＝1＋1＝2；‎ 判断2＞3是否满足？否，返回运算，a2＝2S＝4，S＝a2＝4，i＝3；‎ 判断3＞3是否满足？否，返回运算，a3＝2S＝8.‎ 因此a1＝2，a2＝4，a3＝8，只有C选项符合.‎ ‎12.如图所示是用模拟方法估计圆周率π值的程序框图，P表示估计结果，则图中空白框内应填入(　　)‎ A.P＝ B.P＝ C.P＝ D.P＝ 答案　D 解析　∵xi，yi为0～1之间的随机数，构成以1为边长的正方形面，‎ 当x＋y≤1时，点(xi，yi)均落在以原点为圆心，以1为半径且在第一象限的圆内，当x＋y>1时对应点落在阴影部分中(如图所示).‎ ‎∴＝，Nπ＝4M－Mπ，π(M＋N)＝4M，π＝.‎ ‎13.(2016·全国Ⅱ)中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图.执行该程序框图，若输入的x＝2，n＝2，依次输入的a为2，2，5，则输出的s等于(　　)‎ A.7B.12C.17D.34‎ 答案　C 解析　由框图可知，输入x＝2，n＝2，a＝2，s＝2，k＝1，不满足条件；a＝2，s＝4＋2＝6，k＝2，不满足条件；a＝5，s＝12＋5＝17，k＝3，满足条件，输出s＝17，故选C.‎ ‎14.执行如图所示的程序框图，若输入x＝10，则输出y的值为________.‎ 答案　－ 解析　当x＝10时，y＝×10－1＝4，此时|y－x|＝6＞1，不符合条件；‎ 当x＝4时，y＝×4－1＝1，此时|y－x|＝3＞1，不符合条件；‎ 当x＝1时，y＝×1－1＝－，此时|y－x|＝＞1，不符合条件；‎ 当x＝－时，y＝×－1＝－，此时|y－x|＝＜1，符合条件，所以输出y的值为－.‎ ‎15.执行如图所示的程序框图，当输入m＝－4时，输出的结果为n.若变量x，y满足则目标函数 ＝2x＋y的最大值为________.‎ 答案　5‎ 解析　由程序框图可知，当输入m＝－4时，输出的结果为n＝1，所以变量x，y满足此不等式组表示的可行域如图中的阴影部分所示.由图可知目标函数 ＝2x＋y在点A(2，1)处取得最大值2×2＋1＝5.‎ ‎1.(2017·广州一模)阅读如图的程序框图.若输入n＝5，则输出k的值为(　　)‎ A.2B.3C.4D.5‎ 答案　B 解析　经过第一次循环得到的结果为k＝0，n＝16，‎ 经过第二次循环得到的结果为k＝1，n＝49，‎ 经过第三次循环得到的结果为k＝2，n＝148，‎ 经过第四次循环得到的结果为k＝3，n＝445，满足判断框中的条件，执行“是”输出的k为3.‎ ‎2.执行如图所示的程序框图，若输出k的值为8，则判断框内可填入的条件是(　　)‎ A.s≤？B.s≤？C.s≤？D.s≤？‎ 答案　C 解析　由s＝0，k＝0满足条件，则k＝2，s＝，满足条件；k＝4，s＝＋＝，满足条件；k＝6，s＝＋＝，满足条件；k＝8，s＝＋＝，不满足条件，输出k＝8，所以应填“s≤？”.‎ ‎3.(2017·原创押题预测卷)运行如图所示的程序框图，若输出的结果为，则判断框内不可以填(　　)‎ A.k>2016? B.k≥2016?C.k≥2017? D.k＞2017?‎ 答案　D 解析　执行程序框图可知，该程序是计算＝各项的和，即s＝＝‎ ，当k＝2015时，s＝，则判断框内不可以填k≥2017？故选D.‎ 解题秘籍　(1)程序运行的输出结果可以模拟运行的过程，列出了一步运行后变量的取值.‎ ‎(2)循环结构要把握循环中止的条件，注意赋值的先后顺序不同对变量取值的影响.‎ ‎1.(2017·甘肃一模)关于如图两个程序框图，说法正确的是(　　)‎ A.(1)和(2)都是顺序结构 B.(1)和(2)都是条件分支结构 C.(1)是当型循环结构，(2)是直到型循环结构 D.(1)是直到型循环结构，(2)是当型循环结构 答案　C 解析　观察图(1)，它是先判断后循环，故是当型循环的程序框图；观察图(2)，它是先循环后判断，故是直到型循环的程序框图.‎ ‎2.根据如图所示的程序框图，若输出的y的值是4，则输入的实数x的值为(　　)‎ A.1B.－2C.1或2D.1或－2‎ 答案　D 解析　当x＜1时，由x2＝4，得x＝－2；当1≤x＜10时，由3x＋1＝4，得x＝1；当x≥10时，cosx＝4不可能.‎ ‎3.若如图所示框图所给的程序运行结果为S＝35，那么判断框中应填入的关于k的条件是(　　)‎ A.k＝7? B.k≤6?C.k＜6? D.k＞6?‎ 答案　D 解析　要实现所求算法，框图中最后一次执行循环体时k的值应为6，结合满足条件时执行循环体知当k＝6＞6时就会终止循环，所以判断框内的条件，可为k＞6？.‎ ‎4.(2016·全国Ⅰ)执行下面的程序框图，如果输入的x＝0，y＝1，n＝1，则输出x，y的值满足(　　)‎ A.y＝2xB.y＝3xC.y＝4xD.y＝5x 答案　C 解析　执行题中的程序框图知，‎ 第一次进入循环体：x＝0＋＝0，y＝1×1＝1，x2＋y2<36；‎ 第二次执行循环体：n＝1＋1＝2，x＝0＋＝，y＝2×1＝2，x2＋y2<36；‎ 第三次执行循环体：n＝2＋1＝3，x＝＋＝，y＝3×2＝6，x2＋y2>36，满足x2＋y2≥36，故退出循环，输出x＝，y＝6，满足y＝4x，故选C.‎ ‎5.(2017·北京)执行如图所示的程序框图，输出的s的值为(　　)‎ A.2B.C.D. 答案　C 解析　开始：k＝0，s＝1；‎ 第一次循环：k＝1，s＝2；‎ 第二次循环：k＝2，s＝；‎ 第三次循环：k＝3，s＝，‎ 此时不满足循环条件，输出s，‎ 故输出的s的值为.‎ 故选C.‎ ‎6.执行如图所示的程序框图，若要使输入的x值与输出的y值相等，则这样的x值的个数是(　　)‎ A.1B.2C.3D.4‎ 答案　D 解析　该程序的功能是计算并输出分段函数y＝的函数值，当x≤1时，由x3＝x，解得x＝－1或x＝0或x＝1，这三个x值均满足条件；‎ 当1＜x≤3时，由3x－3＝x，解得x＝，满足条件；‎ 当x＞3时，由＝x，解得x＝－1或x＝1，这两个x值均不满足条件.‎ 综上所述，满足条件的x值的个数是4，故选D.‎ ‎7.(2017·乌鲁木齐模拟)某程序框图如图所示，若输出的S＝26，则判断框内应填(　　)‎ A.k＞3? B.k＞4?C.k＞5? D.k＞6?‎ 答案　A 解析　第一次循环：k＝2，S＝4；‎ 第二次循环：k＝3，S＝11；‎ 第三次循环：k＝4，S＝26；‎ 若输出S＝26，则应该退出循环，故判断框内可填k＞3？.‎ ‎8.某市乘坐出租车的收费办法如下：不超过4千米的里程收费12元；超过4千米的里程按每千米2元收费(对于其中不足千米的部分，若其小于0.5千米则不收费，若其大于或等于0.5千米则按1千米收费)；当车程超过4千米时，另收燃油附加费1元.相应系统收费的程序框图如图所示，其中x(单位：千米)为行驶里程，y(单位：元)为所收费用，用[x]表示不大于x的最大整数，则图中①处应填(　　)‎ A.y＝2＋4B.y＝2＋5C.y＝2＋4D.y＝2＋5‎ 答案　D 解析　由题意，得当x＞4时，所收费用y＝12＋×2＋1＝2＋5，故选D.‎ ‎9.执行如图所示的程序框图，如果输入的t＝0.01，则输出的n等于(　　)‎ A.5B.6C.7D.8‎ 答案　C 解析　执行程序：‎ S＝，m＝，n＝1，S＞t；S＝，m＝，n＝2，S＞t；‎ S＝，m＝，n＝3，S＞t；S＝，m＝，n＝4，S＞t；‎ S＝，m＝，n＝5，S＞t；S＝，m＝，n＝6，S＞t；‎ S＝，m＝，n＝7，此时S＞t不成立，退出循环，n＝7.‎ ‎10.(2016·四川)秦九韶是我国南宋时期的数 家，普州(现四川省安岳县)人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3，2，则输出v的值为(　　)‎ A.9B.18C.20D.35‎ 答案　B 解析　初始值n＝3，x＝2，程序运行过程如下：‎ v＝1，‎ i＝2→v＝1×2＋2＝4，‎ i＝1→v＝4×2＋1＝9，‎ i＝0→v＝9×2＋0＝18，‎ i＝－1，跳出循环，输出v＝18，故选B.‎ ‎11.(2017·山东)执行两次如图所示的程序框图，若第一次输入的x的值为7，第二次输入的x的值为9，则第一次、第二次输出的a的值分别为(　　)‎ A.0，0 B.1，1‎ C.0，1 D.1，0‎ 答案　D 解析　当x＝7时，∵b＝2，∴b2＝4＜7＝x.‎ 又7不能被2整除，∴b＝2＋1＝3.‎ 此时b2＝9＞7＝x，∴退出循环，a＝1，∴输出a＝1.‎ 当x＝9时，∵b＝2，∴b2＝4＜9＝x.‎ 又9不能被2整除，∴b＝2＋1＝3.‎ 此时b2＝9＝x，又9能被3整除，∴退出循环，a＝0.‎ ‎∴输出a＝0.‎ 故选D.‎ ‎12.(2017·全国Ⅰ)如图所示的程序框图是为了求出满足3n－2n>1000的最小偶数n，那么在◇和▭两个空白框中，可以分别填入(　　)‎ A.A>1000？和n＝n＋1 B.A>1000？和n＝n＋2‎ C.A≤1000？和n＝n＋1 D.A≤1000？和n＝n＋2‎ 答案　D 解析　因为题目要求的是“满足3n－2n>1 000的最小偶数n”，所以n的叠加值为2，所以▭内填入“n＝n＋2”.由程序框图知，当◇内的条件不满足时，输出n，所以◇内填入“A≤1000？”.故选D.‎