- 2021-06-15 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019年高考真题——理科数学(天津卷)原卷版
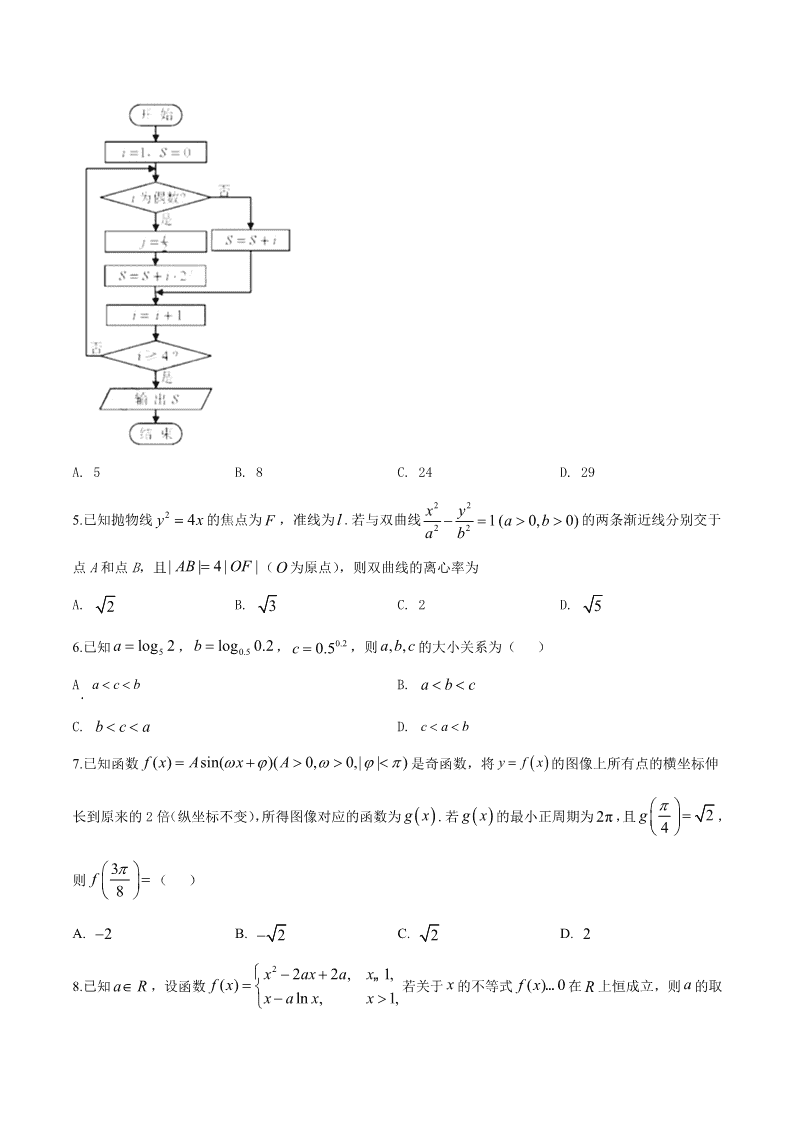
2019 年普通高等学校招生全国统一考试(天津卷) 数学(理工类) 第Ⅰ卷 注意事项: 1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干 净后,再选涂其他答案标号。 2.本卷共 8 小题。 参考公式: ·如果事件 、 互斥,那么 . ·如果事件 、 相互独立,那么 . ·圆柱的体积公式 ,其中 表示圆柱的底面面积, 表示圆柱的高. ·棱锥的体积公式 ,其中 表示棱锥的底面面积, 表示棱锥的高. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合 , , ,则 A. {2} B. {2,3} C. {-1,2,3} D. {1,2,3,4} 2.设变量 满足约束条件 ,则目标函数 的最大值为 A. 2 B. 3 C. 5 D. 6 3.设 ,则“ ”是“ ”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C. 充要条件 D. 既不充分也不必要条件 4.阅读右边的程序框图,运行相应的程序,输出 的值为 A B ( ) ( ) ( )P A B P A P B A B ( ) ( ) ( )P AB P A P B V Sh S h 1 3V Sh S h 1,1,2,3,5A 2,3,4B { |1 3}C x R x „ ( )A C B ,x y 2 0, 2 0, 1, 1, x y x y x y … … 4z x y x R 2 5 0x x | 1| 1x S A. 5 B. 8 C. 24 D. 29 5.已知抛物线 的焦点为 ,准线为 .若与双曲线 的两条渐近线分别交于 点 A 和点 B,且 ( 为原点),则双曲线的离心率为 A. B. C. 2 D. 6.已知 , , ,则 的大小关系为( ) A B. C. D. 7.已知函数 是奇函数,将 的图像上所有点的横坐标伸 长到原来的 2 倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 , 则 ( ) A. B. C. D. 8.已知 ,设函数 若关于 的不等式 在 上恒成立,则 的取 2 4y x F l 2 2 2 2 1( 0, 0)x y a ba b | | 4 | |AB OF O 2 3 5 5log 2a 0.5log 0.2b 0.20.5c , ,a b c . a c b a b c b c a c a b ( ) sin( )( 0, 0,| | )f x A x A y f x g x g x 2π 24g 3 8f 2 2 2 2 a R 2 2 2 , 1,( ) ln , 1, x ax a xf x x a x x „ x ( ) 0f x … R a 值范围为( ) A. B. C. D. 第Ⅱ卷 二.填空题:本大题共 6 小题. 9. 是虚数单位,则 值为__________. 10. 是展开式中的常数项为________. 11.已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面的圆周经过四棱锥四条侧 棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________. 12.设 ,直线 和圆 ( 为参数)相切,则 的值为____. 13.设 ,则 的最小值为______. 14. 在四边形 中, , , , ,点 在线段 延长线上, 且 ,则 __________. 三.解答题.解答应写出文字说明,证明过程或演算步骤. 15. 在 中,内角 所对 边分别为 .已知 , . (Ⅰ)求 的值; (Ⅱ)求 的值. 16.设甲、乙两位同学上学期间,每天 7:30 之前到校的概率均为 .假定甲、乙两位同学到校情况互不影响, 且任一同学每天到校情况相互独立. (Ⅰ)用 表示甲同学上学期间的三天中 7:30 之前到校的天数,求随机变量 的分布列和数学期望; (Ⅱ)设 为事件“上学期间的三天中,甲同学在 7:30 之前到校的天数比乙同学在 7:30 之前到校的天 数恰好多 2”,求事件 发生的概率. 17.如图, 平面 , , . 0,1 0,2 0,e 1,e i 5 1 i i 的 8 3 12 8x x 2 5 a R 2 0ax y 2 2cos , 1 2sin x y a 0, 0, 2 5x y x y ( 1)(2 1)x y xy ABCD AD BC∥ 2 3AB 5AD 30A E CB 的 AE BE BD AE VABC A B C, , 的 , ,a b c 2b c a 3 sin 4 sinc B a C cos B sin 2 6B 2 3 X X M M AE ABCD ,CF AE AD BC∥ ∥ , 1, 2AD AB AB AD AE BC (Ⅰ)求证: 平面 ; (Ⅱ)求直线 与平面 所成角的正弦值; (Ⅲ)若二面角 的余弦值为 ,求线段 的长. 18.设椭圆 的左焦点为 ,上顶点为 .已知椭圆的短轴长为 4,离心率为 . (Ⅰ)求椭圆的方程; (Ⅱ)设点 在椭圆上,且异于椭圆的上、下顶点,点 为直线 与 轴的交点,点 在 轴的负半轴 上.若 ( 为原点),且 ,求直线 的斜率. 19.设 是等差数列, 是等比数列.已知 . (Ⅰ)求 和 的通项公式; (Ⅱ)设数列 满足 其中 . (i)求数列 的通项公式; (ii)求 . 20.设函数 为 的导函数. (Ⅰ)求 单调区间; (Ⅱ)当 时,证明 ; (Ⅲ)设 为函数 在区间 内的零点,其中 ,证明 BF∥ ADE CE BDE E BD F 1 3 CF 2 2 2 2 1( 0)x y a ba b F B 5 5 P M PB x N y | | | |ON OF O OP MN PB na nb 1 1 2 2 3 34, 6 2 2, 2 4a b b a b a , na nb nc 1 1 1, 2 2 ,1, , 2 , k k n k k nc c b n *k N 2 2 1n na c 2 * 1 n i i i a c n N ( ) e cos , ( )xf x x g x f x f x 的 ,4 2x ( ) ( ) 02f x g x x … nx ( ) ( ) 1u x f x 2 ,24 2m m n N . 2 0 0 2 2 sin cos n nn x x e x 查看更多