2015年数学理高考课件6-5 合情推理与演绎推理

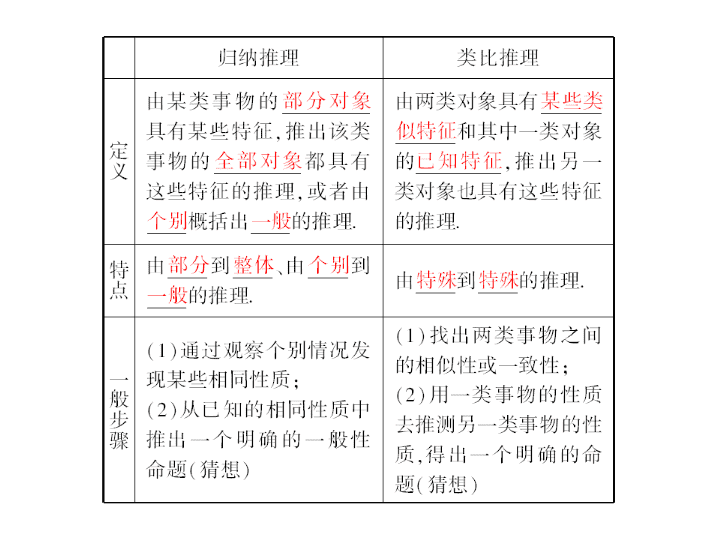
2015年数学理高考课件6-5 合情推理与演绎推理

[ 最新考纲展示 ] 　 1 ． 了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发现中的作用．　 2. 了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理．　 3. 了解合情推理和演绎推理之间的联系和差异． 第五节　合情推理与演绎推理 合情推理 1 ．归纳推理与类比推理 2. 合情推理的作用 合情推理得出的结论具有猜测性，不一定正确，但是，在数学研究中，得到一个新结论之前，合情推理能帮助猜测和发现结论；证明一个数学结论之前，合情推理能提供证明的思路和方向． ____________________[ 通关方略 ]____________________ 1 ．合情推理是合乎情理的推理，它包括归纳推理和类比推理，它们都是根据已有的事实，经过观察、分析、比较、联想，再进行归纳、类比，然后提出猜想的推理． 2 ．在进行类比推理时，要尽量从本质上去类比，不要被表面现象所迷惑，否则只抓住一点表面现象甚至假象就去类比，就会犯机械类比的错误． 答案： D 2 ．数列 {1,2,2,3,3,3,4,4,4,4,5 ， … } 的首项是 1 ，随后两项都是 2 ，接下来 3 项都是 3 ，再接下来 4 项都是 4 ， … ，依此类推，若 a n － 1 ＝ 20 ， a n ＝ 21 ，则 n ＝ ________. 答案： 211 演绎推理 1 ．定义：从 出发，推出 下的结论，我们把这种推理称为演绎推理； 2 ．特点：演绎推理是由 的推理； 3 ．模式：三段论． “ 三段论 ” 是演绎推理的一般模式，包括： 一般性的原理 某个特殊情况 一般到特殊 ____________________[ 通关方略 ]____________________ 在数学中，通常由已知条件归纳出一个结论，或运用类比推理给出某个结论，再运用演绎推理进行严格证明．也就是说，合情推理的结论需要演绎推理的验证，而演绎推理的内容一般是通过合情推理获得的．在前提和推理形式都正确的情况下，通过演绎推理所推出的结论一定是正确的． 3 ．命题 “ 有些有理数是无限循环小数，整数是有理数，所以整数是无限循环小数 ” 是假命题，推理错误的原因是 ( 　　 ) A ．使用了归纳推理 B ．使用了类比推理 C ．使用了 “ 三段论 ” ，但推理形式错误 D ．使用了 “ 三段论 ” ，但小前提错误 解析： 由条件知，使用了三段论，但推理形式是错误的． 答案： C 归纳推理 【 例 1】 　 (2013 年高考陕西卷 ) 观察下列等式 1 2 ＝ 1 1 2 － 2 2 ＝－ 3 1 2 － 2 2 ＋ 3 2 ＝ 6 1 2 － 2 2 ＋ 3 2 － 4 2 ＝－ 10 …… 照此规律，第 n 个等式可为 ____________ ． 解析： 由条件知 n ＋ ( n ＋ 1) ＋ ( n ＋ 2) ＋ … ＋ (3 n － 2) ＝ (2 n － 1) 2 . 答案： n ＋ ( n ＋ 1) ＋ ( n ＋ 2) ＋ … ＋ (3 n － 2) ＝ (2 n － 1) 2 . 反思总结 常见的归纳推理分为数的归纳和形的归纳两类 (1) 数的归纳包括数学归纳和式子归纳，解决此类问题时，需要细心观察，寻求相邻项及项与序号之间的关系，同时还要联系相关的知识，如等差数列、等比数列等． (2) 形的归纳主要包括图形数目归纳和图形变化规律归纳． 变式训练 1 ．用火柴棒摆 “ 金鱼 ” ，如图所示： 按照上面的规律，第 n 条 “ 金鱼 ” 需要火柴棒的根数为 ________ ． 解析： 由图形间的关系可以看出，第一个图中有 8 根火柴棒，第二个图中有 8 ＋ 6 根火柴棒，第三个图中有 8 ＋ 2 × 6 根火柴棒，以此类推第 n 个 “ 金鱼 ” 需要火柴棒的根数是 8 ＋ 6( n － 1) ，即 6 n ＋ 2. 答案： 6 n ＋ 2 类比推理 反思总结 类比推理的应用一般为类比定义、类比性质和类比方法 (1) 类比定义：在求解由某种熟悉的定义产生的类比推理型试题时，可以借助原定义来求解． (2) 类比性质：从一个特殊式子的性质、一个特殊图形的性质入手，提出类比推理型问题，求解时要认真分析两者之间的联系与区别，深入思考两者的转化过程是求解的关键； (3) 类比方法：有一些处理问题的方法具有类比性，我们可以把这种方法类比应用到其他问题的求解中，注意知识的迁移． 解析： 通过类比，等比数列的商对应等差数列的差，应是 ( r － s ) b t ＋ ( s － t ) b r ＋ ( t － r ) b s ＝ 0 ，经验证等式成立． 答案： ( r － s ) b t ＋ ( s － t ) b r ＋ ( t － r ) b s ＝ 0. 演绎推理 反思总结 演绎推理是由一般到特殊的推理，常用的一般模式为三段论，演绎推理的前提和结论之间有着某种蕴含关系，解题时要找准正确的大前提，一般地，若大前提不明确时，可找一个使结论成立的充分条件作为大前提． 解析： y ＝ a x 是增函数这个大前提是错误的，从而导致结论错． 答案： A —— 合情推理与证明的交汇创新问题 合情推理与证明的交汇问题是近年来高考命题的又一创新点，如 2012 年福建高考三角恒等式的推理与证明相结合出现在解答题中，解决此类问题首先要通过观察特例发现某些相似性，然后把这种相似性推广到一个明确表达的一般命题，最后进行证明检验． 【 典例 】 　某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数： ① sin 2 13° ＋ cos 2 17° － sin 13°cos 17° ； ② sin 2 15° ＋ cos 2 15° － sin 15°cos 15° ； ③ sin 2 18° ＋ cos 2 12° － sin 18°cos 12° ； ④ sin 2 ( － 18°) ＋ cos 2 48° － sin( － 18°)cos 48° ； ⑤ sin 2 ( － 25°) ＋ cos 2 55° － sin( － 25°)cos 55°. (1) 试从上述五个式子中选择一个，求出这个常数； (2) 根据 (1) 的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论． 由题悟道 解决本题的关键 (1) 正确应用三角恒等变换，用一个式子把常数求出来． (2) 通过观察各个等式的特点，找出共性，利用归纳推理正确得出一个三角恒等式，并给出正确的证明． 本小节结束 请按 ESC 键返回