数学文卷·2018届河南省安阳二中高二下学期期末考试(2017-07)
安阳市第二中学2016-2017学年第二学期期末考试
高二数学(文科)试卷
命题人:罗红梅 审题人:程学连
一、选择题(本大题共20小题,在每小题所给的四个选项中有且只有一项是符合要求的,请用2B铅笔将答题卡上该项的小方框涂黑. 每小题5分,共100分.)
1.函数y=的定义域是( )
A. [1,+∞) B.() C. D.(﹣∞,1]
2.设复数,则|z|=( ).
A. B. C. D.2
3.已知a,b>0且a≠1,b≠1,若logab>1,则( )
A.(a-1)(b-1)<0 B.(a-1)(a-b)>0
C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
4.已知曲线在点处切线的斜率为1,则实数的值为( )
A. B. C. D.
5.函数f(x)=x2﹣的零点有( )个.
A.1 B.2 C.3 D.4
6.已知函数f(x)=若f(-a)+f(a)≤2f(1),则实数a的取值范围是( )
A.[0,1] B.[-1,0)
C.[-1,1] D.[-1,0]
7.设各项都是正数的等比数列{an},Sn为前n项和,且S10=10,S30=70,那么S40等于( )
A.150 B.-200
C.150或-200 D.400或-50
8. 在中,=60,AB=2,且,则BC边的长为( )
A. B.3 C. D.7
9.若两个非零向量a,b满足|a+b|=|a-b|=2|a|,则向量b与a+b的夹角为( )
A. B.
C. D.
10.设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n-1+a2n<0”的( )
A.充要条件 B.充分而不必要条件
C.必要而不充分条件 D.既不充分也不必要条件
11.已知非零向量m,n满足4|m|=3|n|,cos
=,若n⊥(tm+n),则实数t的值为( )
A.4 B.-4 C D.
12.将函数的图象向左平移个单位长度,所的图象对应的函数( )
A. 在区间上单调递减B. 在区间上单调递增
C. 在区间上单调递减 D. 在区间上单调递增
13.将函数的图像向右平移个单位后得到函数的图像,对满足的,,有,则( )
A. B. C. D.
14.+++…+的值为( )
A. B.-
C.- D.-+
15.函数,则( )
A.为函数的极大值点 B.为函数的极小值点
C. 为函数的极大值点 D.为函数的极小值点
16.已知函数,其导函数记为,则
( )
A.0 B.1 C. 2 D.2017511
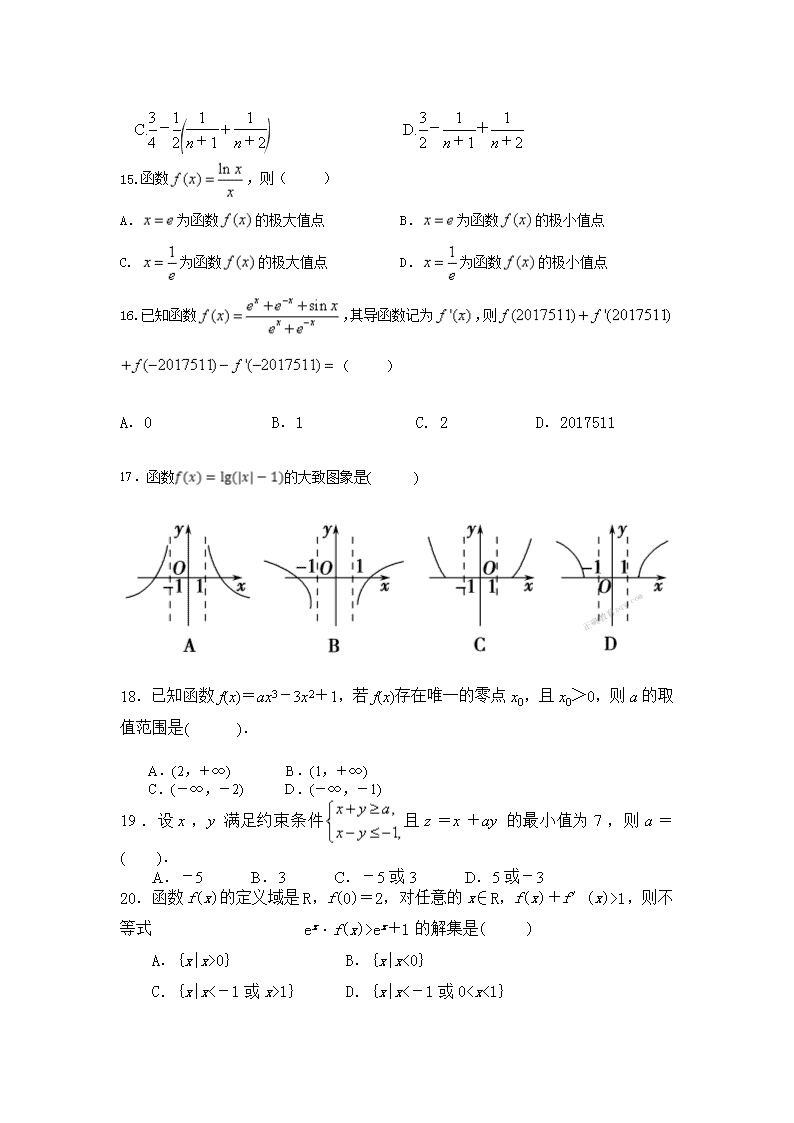
17.函数的大致图象是( )
18.已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ).
A.(2,+∞) B.(1,+∞)
C.(-∞,-2) D.(-∞,-1)
19.设x,y满足约束条件且z=x+ay的最小值为7,则a=( ).
A.-5 B.3 C.-5或3 D.5或-3
20.函数f(x)的定义域是R,f(0)=2,对任意的x∈R,f(x)+f′(x)>1,则不等式 ex·f(x)>ex+1的解集是( )
A.{x|x>0} B.{x|x<0}
C.{x|x<-1或x>1} D.{x|x<-1或0y>0,且xy=2,若不等式-4mx+4my≥0恒成立,则实数m的取值范围为
.
三、解答题(本大题共3小题,请在答题卡相应区域内答题,解答要写出必要的文字说明、证明过程和推演步骤. 共30分.)
26.已知函数,(其中)的图象与轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(1)求的解析式;
(2)当时,求的值域。
27.(本小题满分12分)(2014课标全国Ⅰ,文17)已知{an}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.
(1)求{an}的通项公式;
(2)求数列的前n项和.
28. 设函数.
(1)当时,讨论函数的单调性;
(2)若对任意及任意,,恒有成立,求实数的取值范围.
安阳市第二中学2016-2017学年第二学期期末考试
高二数学文科试卷答案
一、选择题(本大题共20小题,在每小题所给的四个选项中都有且只有一项是符合要求的,请用2B铅笔将答题卡上该项的小方框涂黑. 每小题5分,共100分.)
1----5 CBDDC 6—10 CAAAC 11—15 BBDCA 16—20 CBCBA
二、填空题(本大题共5小题,每小题4分,共20分.)
21. -1,1,0 22. - 23. an=(n∈N*). 24. (-1,1) 25. (-∞,1]
三、解答题(本大题共3小题,请在答题卡相应区域内答题,解答要写出必要的文字说明、证明过程和推演步骤. 共30分.)
26.已知函数,(其中)的图象与轴的交点中,相邻两个交点之间的距离为,且图象上一个最低点为.
(1)求的解析式;
(2)当时,求的值域。
解:(1)由最低点为M,得A=2.
由x轴上相邻两个交点之间的距离为,得=,
即T=π,∴ω===2.
由点M 在图象上,得2sin=-2,
即sin=-1,故+φ=2kπ-(k∈Z).
∴φ=2kπ-(k∈Z).又φ∈,∴φ=.
故f(x)=2sin.
(2)∵x∈,∴2x+∈.
当2x+=,即x=时, f(x)取得最大值2;
当2x+=,即x=时, f(x)取得最小值-1,
故f(x)的值域为[-1,2].
27.(本小题满分12分)(2014课标全国Ⅰ,文17)已知{an}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.
(1)求{an}的通项公式;
(2)求数列的前n项和.
解:(1)方程x2-5x+6=0的两根为2,3,由题意得a2=2,a4=3.
设数列{an}的公差为d,则a4-a2=2d,故,从而.
所以{an}的通项公式为.
(2)设的前n项和为Sn,由(1)知,则
,
.
两式相减,得.
所以.
28. 设函数.
(1)当时,讨论函数的单调性;
(2)若对任意及任意,,恒有
成立,求实数的取值范围.
28.解:(1),
当,即时,,在上是减函数;
当,即时,令,得或;令,得;
当,即时,令,得或;令,得;
综上,当时,在定义域上是减函数;
当时,在,上单调递减,在上单调递增;
当时,在和上单调递减,在上单调递增.
(2)由(2)知,当时,在上单调递减,
当时,有最大值,当时,有最小值,
对任意,恒有,.
构造函数,则,
,.
函数在上单调增.
,.