数学卷·2018届河北省定州中学高二12月月考（2016-12）

数学卷·2018届河北省定州中学高二12月月考（2016-12）

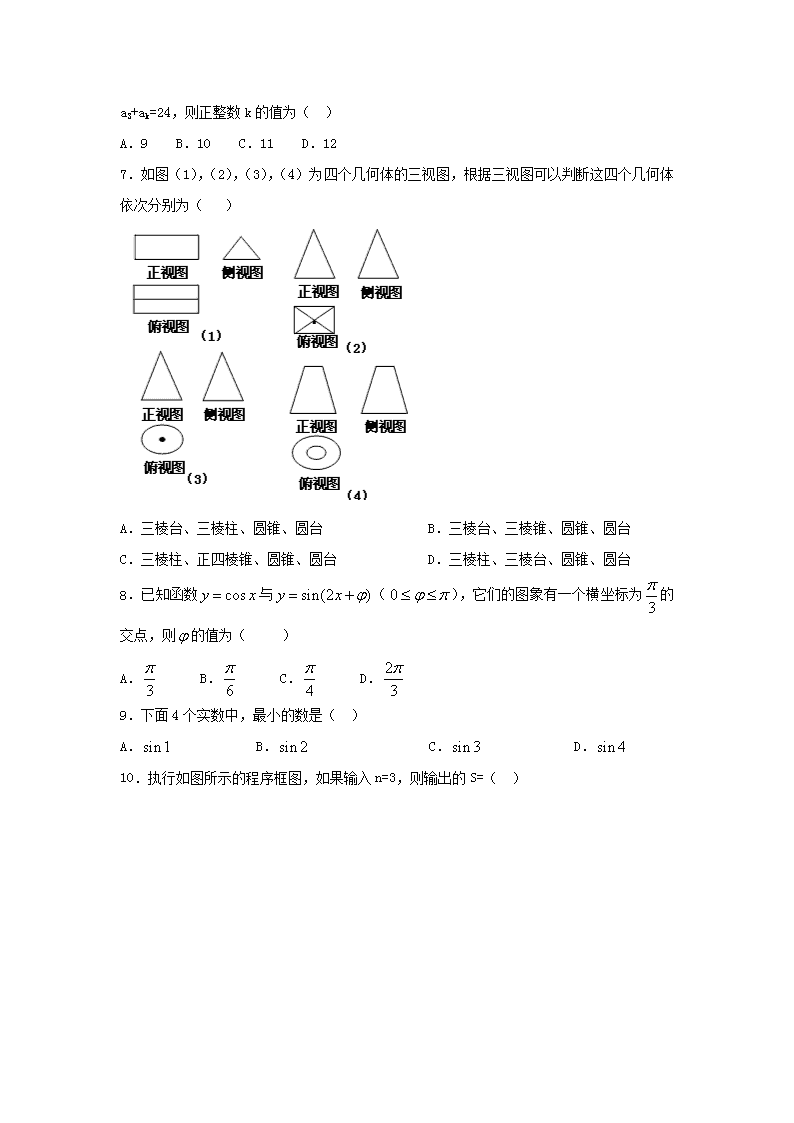
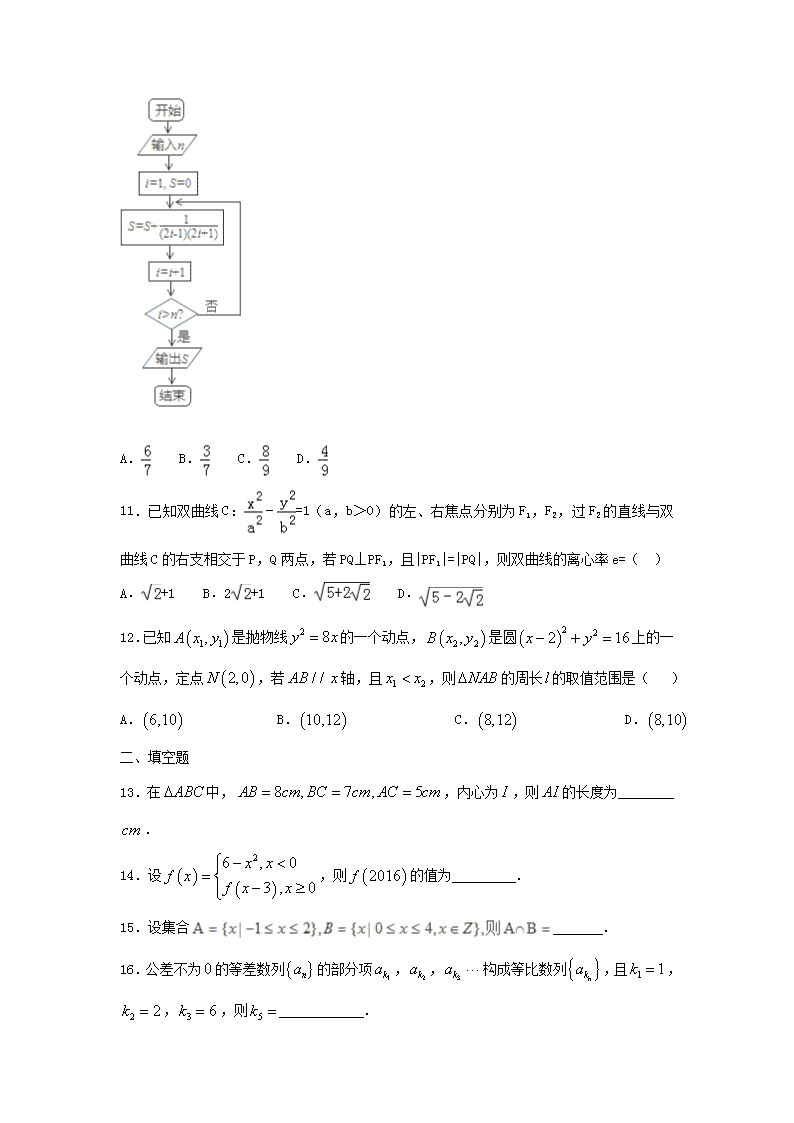
河北定州中学2016-2017学年第一学期高二12月考数学试卷 一、选择题 ‎1．已知数列是等比数列，若，则（ ）‎ A．有最大值 B．有最小值 C．有最大值 D．有最小值 ‎2．若圆与圆关于直线对称，则圆的方程为（ ）‎ A. B. ‎ C. D. ‎ ‎3．若集合，，且，则的值为（ ）[]‎ A. B. ‎ C.或 D.或或 ‎4．已知，那么（ ）‎ A． B． C． D．‎ ‎5．（2015春•咸宁期末）如图是正方体的平面展开图，则在这个正方体中：‎ ‎①BM与ED平行 ‎②CN与BE是异面直线 ‎③CN与BM成60°角 ‎④DM与BN是异面直线 以上四个命题中，正确的命题序号是（ ）‎ A．①②③ B．②④ C．③④ D．②③④‎ ‎6．（2015•河北区二模）设Sn是等差数列{an}的前n项和，公差d≠0，若S11=132，‎ a3+ak=24，则正整数k的值为（ ）‎ A．9 B．10 C．11 D．12‎ ‎7．如图（1），（2），（3），（4）为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（ ）‎ A．三棱台、三棱柱、圆锥、圆台 B．三棱台、三棱锥、圆锥、圆台 C．三棱柱、正四棱锥、圆锥、圆台 D．三棱柱、三棱台、圆锥、圆台 ‎8．已知函数与（），它们的图象有一个横坐标为的交点，则的值为（ ）‎ A． B． C． D．‎ ‎9．下面4个实数中，最小的数是（ ）‎ A． B． C． D．‎ ‎10．执行如图所示的程序框图，如果输入n=3，则输出的S=（ ）‎ A． B． C． D．‎ ‎11．已知双曲线C：﹣=1（a，b＞0）的左、右焦点分别为F1，F2，过F2的直线与双曲线C的右支相交于P，Q两点，若PQ⊥PF1，且|PF1|=|PQ|，则双曲线的离心率e=（ ）‎ A．+1 B．2+1 C． D．‎ ‎12．已知是抛物线的一个动点，是圆上的一个动点，定点，若轴，且，则的周长的取值范围是（ ）‎ A． B． C． D．‎ 二、填空题 ‎13．在中，，内心为，则的长度为________．‎ ‎14．设，则的值为 ．‎ ‎15．设集合 ．‎ ‎16．公差不为的等差数列的部分项，，构成等比数列，且，，，则 ．‎ 三、解答题 ‎17．选修4-1：几何证明选讲 如图，在中，，以为直径的圆交于点，过点作圆的切线交于点．‎ ‎（1）求证：；‎ ‎（2）若，求的大小．‎ ‎18．如图，在边长为4的菱形中，，点分别是边的中点，，沿将翻折到，连接，得到如图的五棱锥，且．‎ ‎（1）求证：；‎ ‎（2）求四棱锥的体积．‎ ‎19．已知命题：，是方程的两个实根，且不等式对任意恒成立；命题：不等式有解，若命题为真，为假，求实数的取值范围．‎ ‎20．已知函数，．‎ ‎（1）当时，解不等式；‎ ‎（2）若对任意，都存在，使得成立，求实数的取值范围．‎ 参考答案 DCDCC ACBDB ‎11．D ‎12．C ‎13．‎ ‎14．‎ ‎15．‎ ‎16．‎ ‎17．（1）证明：由题意可知，均为圆的切线，‎ 所以，连接，易知，‎ 所以，‎ 又，‎ 所以，所以，‎ 所以 ‎（2）解：不妨设，则，‎ 在中，由射影定理可知，，，‎ 所以，∴，所以，‎ 所以，由（1）可知，，∴‎ ‎18．（1）详见解析（2）3‎ ‎（1）证明：∵点分别是边的中点，‎ ‎∴，‎ ‎∵菱形的对角线互相垂直，∴，∴，‎ ‎∴，‎ ‎∵平面平面，‎ ‎∴平面，∴平面，∴‎ ‎（2）解：设，连接，∵，‎ ‎∴为等边三角形，∴，‎ 在中，，‎ 在中，，∴．‎ ‎∵，平面，平面，‎ ‎∴平面，梯形的面积，‎ ‎∴四棱锥的体积．‎ ‎19．．‎ ‎：：等式对任意恒成立 ‎，：显然不是不等式的解，不等式有解，‎ 又∵为真，为假，∴，中一真一假，∴实数的取值范围是．‎ ‎20．（1）；（2）.‎ ‎（1）当时，‎ ‎∴，即或或，‎ ‎∴或，‎ ‎∴不等式的解集为．‎ ‎（2）∵对任意，都存在，使得成立，‎ ‎∴，，‎ ‎（当且仅当时等号成立），‎ ‎，所以，∴或，‎ ‎∴或，∴实数的取值范围为．‎