高考数学专题复习：立体几何精选精练2

高考数学专题复习：立体几何精选精练2

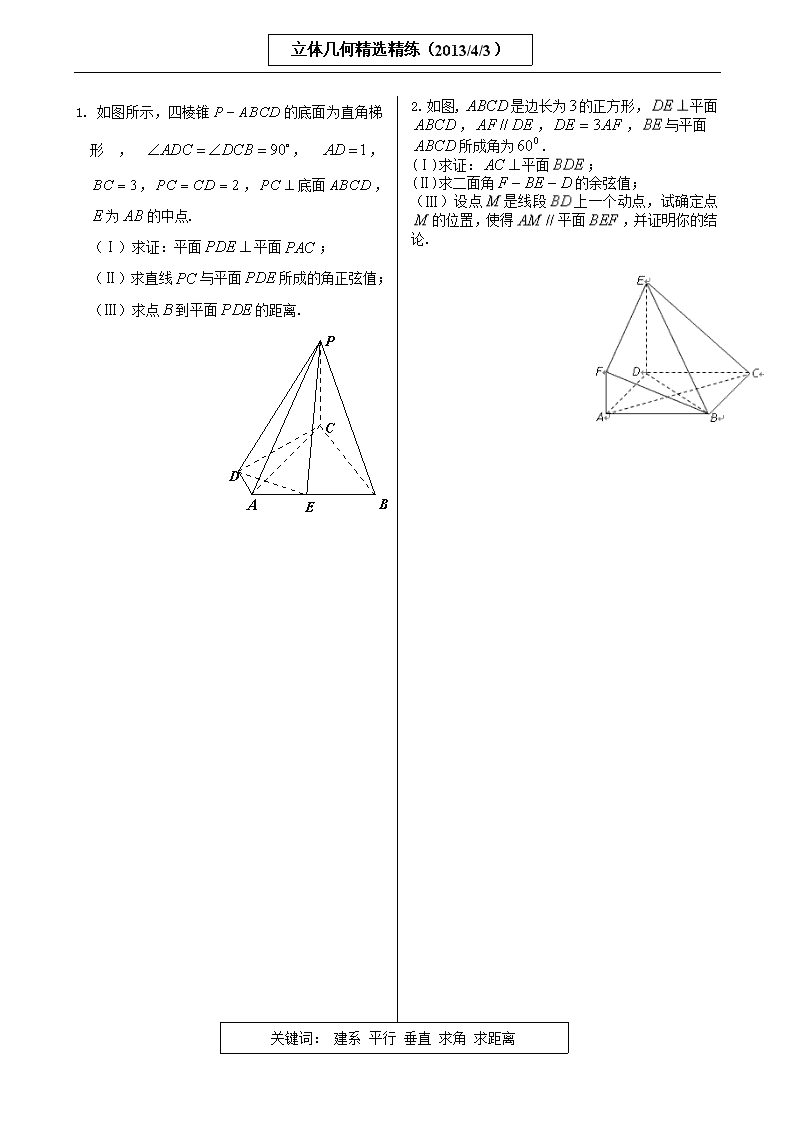
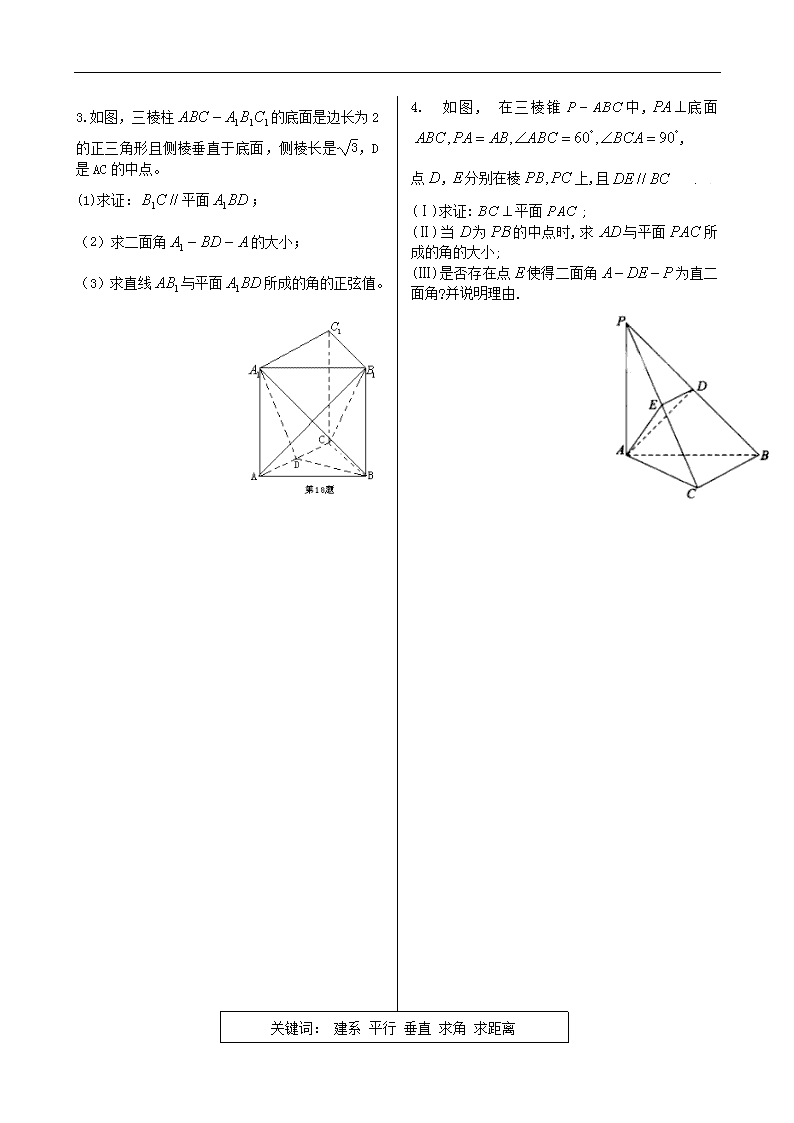
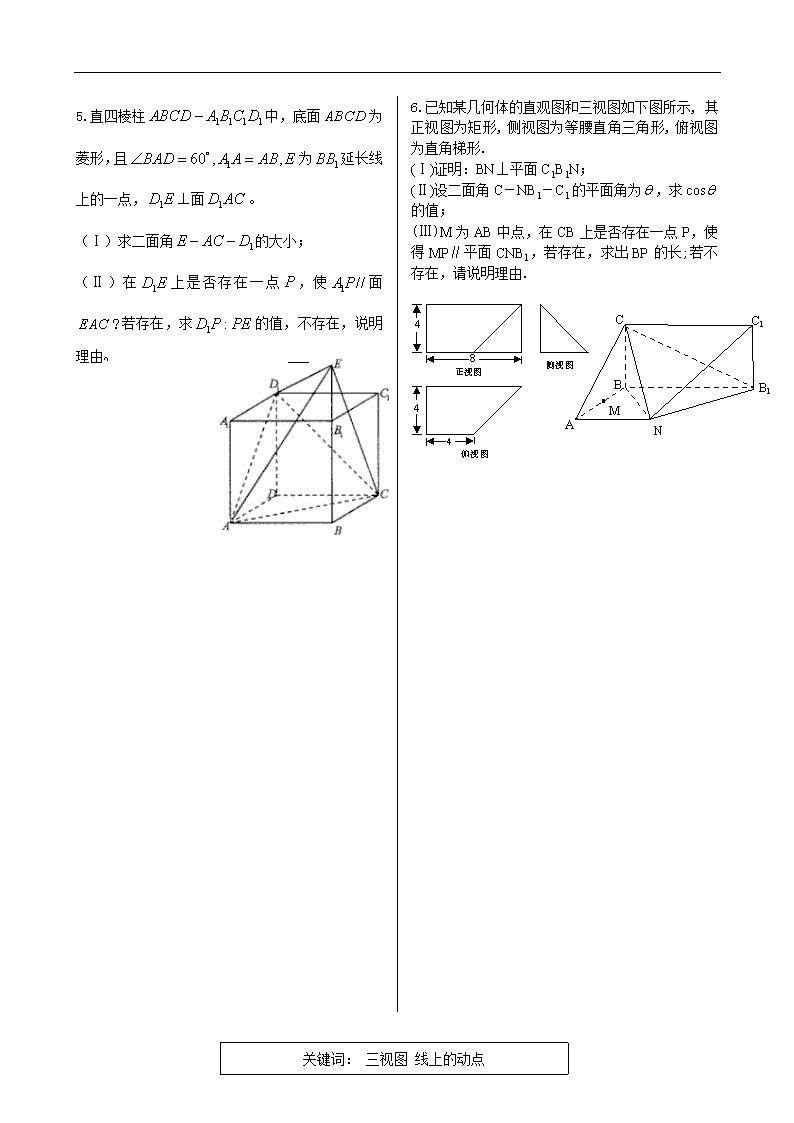
立体几何精选精练（‎2013/4/3‎）‎ ‎1. 如图所示，四棱锥的底面为直角梯形，，，，，底面，为的中点.‎ ‎ （Ⅰ）求证：平面平面；‎ ‎ （Ⅱ）求直线与平面所成的角正弦值；‎ ‎ （Ⅲ）求点到平面的距离.‎ D P E A B C 关键词： 建系 平行 垂直 求角 求距离 ‎2. 如图, 是边长为的正方形，平面，，，与平面所成角为.‎ ‎(Ⅰ)求证：平面；‎ ‎(Ⅱ)求二面角的余弦值；‎ ‎（Ⅲ）设点是线段上一个动点，试确定点的位置，使得平面，并证明你的结论.‎ ‎3.如图，三棱柱的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是，D是AC的中点。‎ ‎(1)求证：平面；　　　　　　　　　　　　　‎ ‎（2）求二面角的大小；‎ ‎（3）求直线与平面所成的角的正弦值。‎ 关键词： 建系 平行 垂直 求角 求距离 ‎4. 如图,在三棱锥中,底面,‎ 点,分别在棱上,且 ‎ ‎(Ⅰ)求证:平面;‎ ‎(Ⅱ)当为的中点时,求与平面所成的角的大小;‎ ‎(Ⅲ)是否存在点使得二面角为直二面角?并说明理由.‎ ‎5.直四棱柱中，底面为菱形，且为延长线上的一点，面。‎ ‎（Ⅰ）求二面角的大小；‎ ‎（Ⅱ）在上是否存在一点，使面?若存在，求的值，不存在，说明理由 关键词： 三视图 线上的动点 ‎6.已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.‎ ‎(Ⅰ)证明：BN⊥平面C1B1N；‎ ‎(Ⅱ)设二面角C－NB1－C1的平面角为，求cos的值；‎ ‎(Ⅲ)M为AB中点，在CB上是否存在一点P，使得MP∥平面CNB1，若存在，求出BP的长;若不存在，请说明理由.‎ N C C1‎ B1‎ B A M ‎7. 四棱锥P－ABCD的底面与四个侧面的形状和大小如图所示。‎ ‎（Ⅰ）写出四棱锥P－ABCD中四对线面垂直关系（不要求证明）；‎ ‎（Ⅱ）在四棱锥P－ABCD中，若E为PA的中点，求证：BE∥平面PCD；‎ ‎（Ⅲ）在四棱锥P－ABCD中，设面PAB与面PCD所成的角为，求的值 关键词： 空间想象 ‎8. 如图，是两条互相垂直的异面直线，点P、C在直线上，点A、B在直线上，M、N分别是线段AB、AP的中点，且PC=AC=a，（I）证明：平面ABC；‎ ‎（II）设平面MNC与平面PBC所成的角为 ‎ 现给出四个条件：‎ ‎ ① ② ‎ ‎③CM ④‎ 请从中再选择两上条件以确定的值，并求之.‎ ‎9. 已知某几何体的三视图如图所示，其中分别是该几何体的一个顶点P在三个投影面上的投影，分别是另四个顶点A，B，C，D的投影。‎ ‎（I）从①②两个图中选择出该几何体的直观图；‎ ‎（II）求直线PA与平面PBC所成角的正弦值；‎ ‎（III）设平面PAD与平面ABC的交线为，求二面角A——B的大小 关键词： 面上的动点 ‎10 . 如图，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=，BC=1，PA=2，E为PD的中点. （Ⅰ）求直线AC与PB所成角的余弦值；‎ ‎（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，并求出N点到AB和AP的距离. ‎ ‎11. 在直角梯形ABCD中，AD//BC，,,如图（1）．把沿翻折，使得平面.‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）若点为线段中点，求点到平面的距离；‎ ‎（Ⅲ）在线段上是否存在点N，使得与平面所成角为？若存在，求出的值；若不存在，说明理由．‎ ‎12 ．如图1，在等腰梯形中，，，，为上一点，且，．将梯形沿折成二面角，设其大小为．‎ ‎（Ⅰ）在上述折叠过程中，若，请你动手实验并直接写出直线与平面所成角的取值范围（不必证明）；‎ ‎（Ⅱ）当时，连结，，，得到如图2所示的几何体，‎ ‎（i）求证：平面平面；‎ ‎（ii）在平面上是否存在点，使得线段的中点在平面上，若存在，试确定点的位置；若不存在，请说明理由．‎ 关键词： 翻折问题 ‎13. 如图所示的几何体中，，，；直角三角形中，， ．‎ ‎（Ⅰ）求与所成角的正弦值；‎ ‎（Ⅱ）若过点且与直线垂直的平面与直线交于点，求线段的长度．‎ 关键词： 函数与最值 ‎14．如图，圆柱内有一个三棱柱，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O直径。‎ ‎（Ⅰ）证明：平面平面；‎ ‎（Ⅱ）设AB=，在圆柱内随机选取一点，记该点取自于三棱柱内的概率为。‎ ‎（i）当点C在圆周上运动时，求的最大值；‎ ‎（ii）记平面与平面所成的角为，当取最大值时，求的值。‎ ‎15．如图，已知平行四边形中，四边形为正方形，平面平面分别是的中点.‎ ‎（Ⅰ）求证：∥平面 ‎（Ⅱ）记表示四棱锥的体积.‎ ‎(ⅰ)求的表达式；‎ ‎（ⅱ）当取得最大值时，求平面与平面所成锐二面角的余弦值.‎ 关键词： 函数与最值 ‎16.如图，侧棱垂直底面的三棱柱中，，，，是侧棱上的动点.‎ ‎（Ⅰ）当时，求证：；‎ ‎（Ⅱ）试求三棱锥的体积取得最大值时的值；‎ ‎（Ⅲ）若二面角的平面角的余弦值为，试求实数的值.‎