高考数学复习专题练习第7讲 函数图像
第7讲 函数图像
一、选择题
1.函数=ln的大致图像为(如图所示) ( ).
解析 y=-ln|2x-3|=
故当x>时,函数为减函数,当x<时,函数为增函数.
答案 A
2.由方程x|x|+y|y|=1确定的函数y=f(x)在(-∞,+∞)上是( ).
A.增函数 B.减函数
C.先增后减 D.先减后增
解析 ①当x≥0且y≥0时,x2+y2=1,②当x>0且y<0时,x2-y2=1,
③当x<0且y>0时,y2-x2=1,
④当x<0且y<0时,无意义.
由以上讨论作图如上图,易知是减函数.
答案 B
3.已知函数f(x)=x-tan x,若实数x0是函数y=f(x)的零点,且0
0,则f(t)>0,故选B.
答案 B
4.如图,正方形ABCD的顶点A,B,顶点C、D位于第一象限,直线l:x=t(0≤t≤)将正方形ABCD分成两部分,记位于直线l左侧阴影部分的面积为f(t),则函数S=f(t)的图象大致是 ( ).
解析 当直线l从原点平移到点B时,面积增加得越来越快;当直线l从点B平移到点C时,面积增加得越来越慢.故选C.
答案 C
5.在同一坐标系中画出函数y=logax,y=ax,y=x+a的图象,可能正确的是( ).
解析 当a>1或0<a<1时,排除C;当0<a<1时,再排除B;当a
>1时,排除A.
答案 D
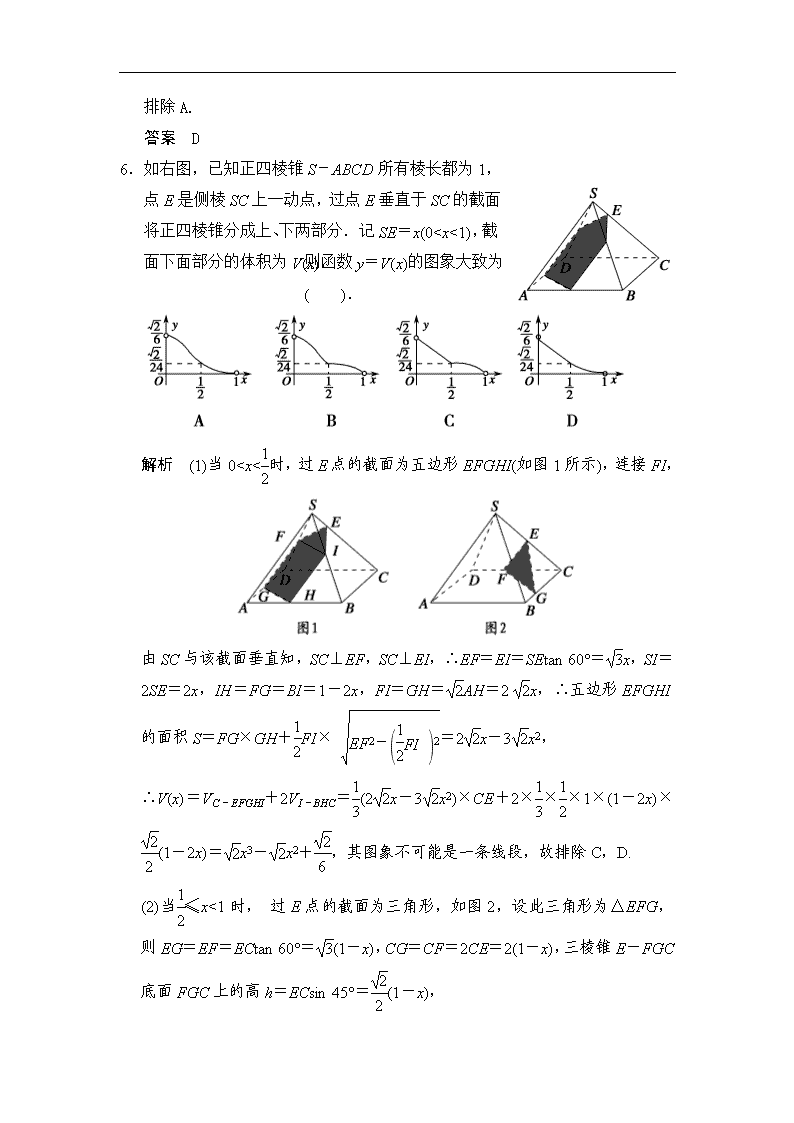
6.如右图,已知正四棱锥S-ABCD所有棱长都为1,
点E是侧棱SC上一动点,过点E垂直于SC的截面将正四棱锥分成上、下两部分.记SE=x(00,且a≠1,f(x)=x2-ax,当x∈(-1,1)时,均有f(x)<,则实数a的取值范围是________.
解析 由题知,当x∈(-1,1)时,f(x)=x2-ax<,即x2 -1时,如图,要使在(1,2)上,f1(x)=(x-1)2的图象在f2(x)=logax的下方,
只需f1(2)≤f2(2),
即(2-1)2≤loga2,loga2≥1,
∴1<a≤2.
∴a的取值范围是(1,2]
14.已知函数f(x)=x|m-x|(x∈R),且f(4)=0.
(1)求实数m的值;
(2)作出函数f(x)的图象并判断其零点个数;
(3)根据图象指出f(x)的单调递减区间;
(4)根据图象写出不等式f(x)>0的解集;
(5)求集合M={m|使方程f(x)=m有三个不相等的实根}.
解 (1)∵f(4)=0,∴4|m-4|=0,即m=4.
(2)∵f(x)=x|m-x|=x|4-x|=
∴函数f(x)的图象如图:
由图象知f(x)有两个零点.
(3)从图象上观察可知:f(x)的单调递减区间为[2,4].
(4)从图象上观察可知:
不等式f(x)>0的解集为:{x|04}.
(5)由图象可知若y=f(x)与y=m的图象有三个不同的交点,则0
查看更多