数学卷·2018届黑龙江省大庆市杜蒙县高二上学期期末考试（2017-01）

数学卷·2018届黑龙江省大庆市杜蒙县高二上学期期末考试（2017-01）

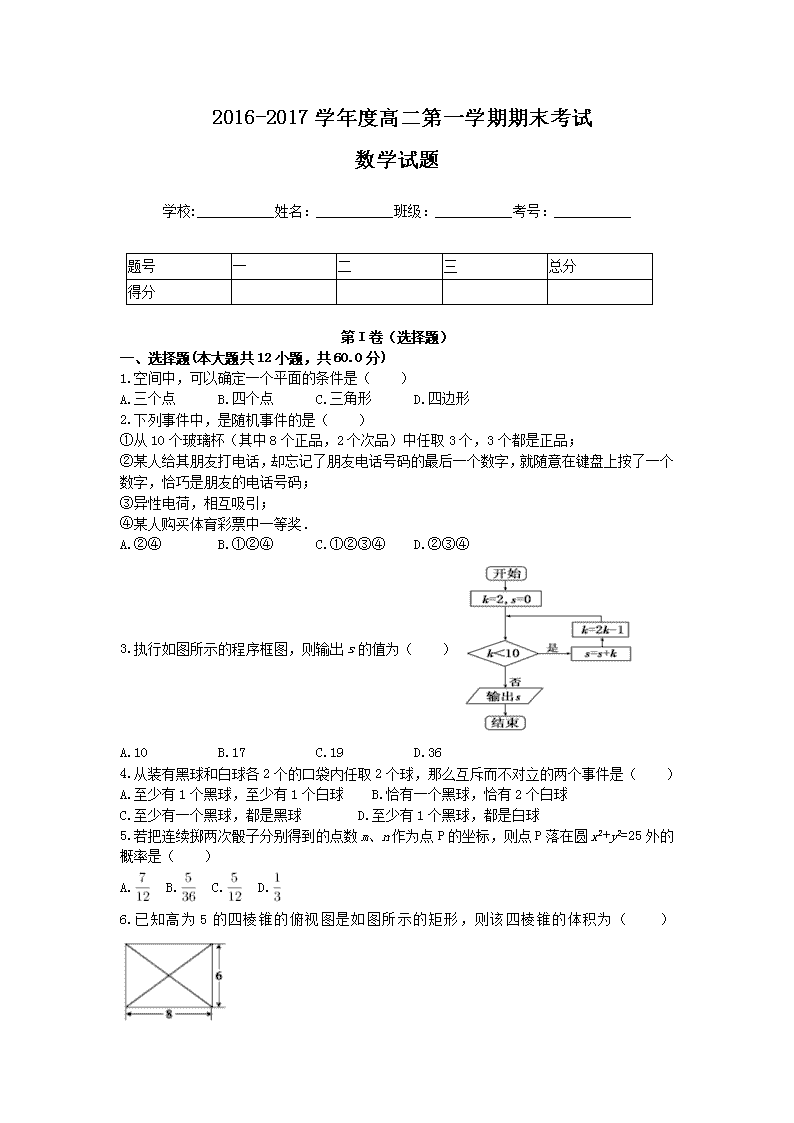
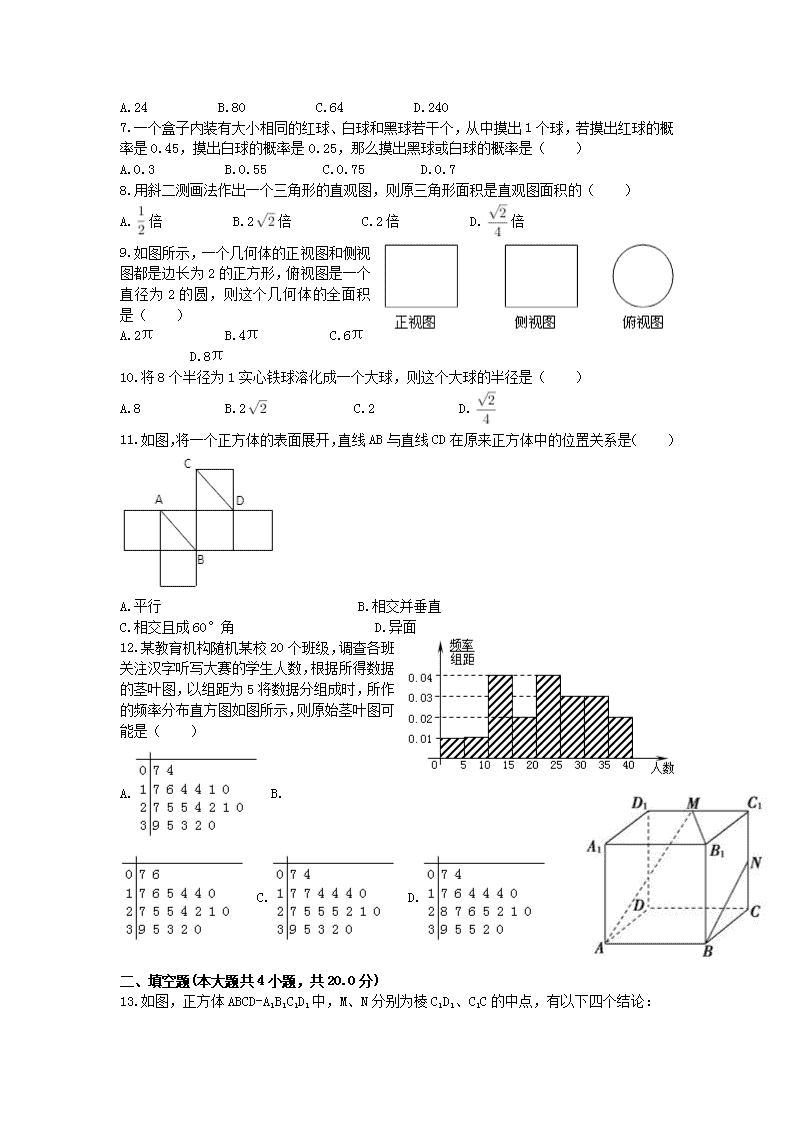
‎ 2016-2017学年度高二第一学期期末考试 数学试题 学校:___________姓名：___________班级：___________考号：___________‎ 题号 一 二 三 总分 得分 ‎ ‎ ‎ ‎ ‎ ‎ ‎  ‎ 第I卷（选择题）‎ 一、选择题(本大题共12小题，共60.0分)‎ ‎1.空间中，可以确定一个平面的条件是（　　） A.三个点   B.四个点   C.三角形   D.四边形 ‎2.下列事件中，是随机事件的是（　　） ①从10个玻璃杯（其中8个正品，2个次品）中任取3个，3个都是正品； ②某人给其朋友打电话，却忘记了朋友电话号码的最后一个数字，就随意在键盘上按了一个数字，恰巧是朋友的电话号码； ③异性电荷，相互吸引； ④某人购买体育彩票中一等奖． A.②④    B.①②④   C.①②③④  D.②③④‎ ‎3.执行如图所示的程序框图，则输出s的值为（　　） A.10     B.17     C.19     D.36‎ ‎4.从装有黑球和白球各2个的口袋内任取2个球，那么互斥而不对立的两个事件是（　　） A.至少有1个黑球，至少有1个白球  B.恰有一个黑球，恰有2个白球 C.至少有一个黑球，都是黑球    D.至少有1个黑球，都是白球 ‎5.若把连续掷两次骰子分别得到的点数m、n作为点P的坐标，则点P落在圆x2+y2=25外的概率是（　　） A. B. C. D.‎ ‎6.已知高为5的四棱锥的俯视图是如图所示的矩形，则该四棱锥的体积为（　　） ‎ ‎ A.24     B.80     C.64     D.240‎ ‎7.一个盒子内装有大小相同的红球、白球和黑球若干个，从中摸出1个球，若摸出红球的概率是0.45，摸出白球的概率是0.25，那么摸出黑球或白球的概率是（　　） A.0.3     B.0.55    C.0.75    D.0.7‎ ‎8.用斜二测画法作出一个三角形的直观图，则原三角形面积是直观图面积的（　　） A.倍     B.2倍     C.2倍     D.倍 ‎9.如图所示，一个几何体的正视图和侧视图都是边长为2的正方形，俯视图是一个直径为2的圆，则这个几何体的全面积是（　　） A.2π     B.4π     C.6π     D.8π ‎10.将8个半径为1实心铁球溶化成一个大球，则这个大球的半径是（　　） A.8      B.2      C.2      D.‎ ‎11.如图，将一个正方体的表面展开，直线AB与直线CD在原来正方体中的位置关系是（　　） A.平行              B.相交并垂直 C.相交且成60°角          D.异面 ‎12.某教育机构随机某校20个班级，调查各班关注汉字听写大赛的学生人数，根据所得数据的茎叶图，以组距为5将数据分组成时，所作的频率分布直方图如图所示，则原始茎叶图可能是（　　） A. B. C. D.‎ 二、填空题(本大题共4小题，共20.0分)‎ ‎13.如图，正方体ABCD-A1B1C1D1中，M、N分别为棱C1D1、C1C的中点，有以下四个结论：‎ ‎ ①直线AM与CC1是相交直线； ②直线AM与BN是平行直线； ③直线BN与MB1是异面直线； ④直线AM与DD1是异面直线． 其中正确的结论为 ______ （注：把你认为正确的结论的序号都填上）．‎ ‎14.过点P（-1，2）且与直线2x+y-5=0平行的直线方程为 ______ ．‎ ‎15.圆x2+y2-2x-2y+1=0上的动点Q到直线3x+4y+8=0距离的最小值为 ______ ．‎ ‎16.假设要考察某公司生产的500克袋装牛奶的三聚青氨是否超标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表第7行第8列的数开始向右读，请你依次写出最先检测的5袋牛奶的编号 ______ （下面摘取了随机数表第7行至第9行） 84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54．‎ 三、解答题(本大题共6小题，共72.0分)‎ ‎17.某公司的广告费支出x与销售额y（单位：万元）之间有下列对应数据 ‎ x ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ y ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ 回归方程为=bx+a，其中b=，a=-b． （1）画出散点图，并判断广告费与销售额是否具有相关关系； （2）根据表中提供的数据，求出y与x的回归方程=bx+a； （3）预测销售额为115万元时，大约需要多少万元广告费． ‎ ‎18.某射击队的队员为在射击锦标赛上取得优异成绩，正在加紧备战，经过近期训练，某队员射击一次，命中7～10环的概率如表所示： ‎ 命中环数 ‎10环 ‎9环 ‎8环 ‎7环 概率 ‎0.30‎ ‎0.28‎ ‎0.18‎ ‎0.12‎ 求该射击队员射击一次， （1）射中9环或10环的概率； （2）至少命中8环的概率； （3）命中不足8环的概率． ‎ 19. 某高校学生总数为8000人，其中一年级1600人，二年级3200人，三年级2000人，四年级1200人．为了完成一项调查，决定采用分层抽样的方法，从中抽取容量为400的样本． （1）各个年级分别抽取了多少人？ （2）若高校教职工有505人，需要抽取50个样本，你会采用哪种抽样方法，请写出具体抽样过程． 20.如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点，求证： （Ⅰ）PA∥平面EDB （Ⅱ）AD⊥PC． ‎ ‎ ‎ 21. 在某中学举行的物理知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15． （1）求成绩在50～70分的频率是多少； （2）求这三个年级参赛学生的总人数是多少； （3）求成绩在80～100分的学生人数是多少． ‎ ‎ ‎ ‎22.已知圆C：（x-1）2+（y-2）2=4． （1）求直线2x-y+4=0被圆C所截得的弦长； （2）求过点M（3，1）的圆C的切线方程． ‎