数学卷·2018届江西省抚州市崇仁二中高二上学期第一次月考数学试卷（文科）（解析版）

数学卷·2018届江西省抚州市崇仁二中高二上学期第一次月考数学试卷（文科）（解析版）

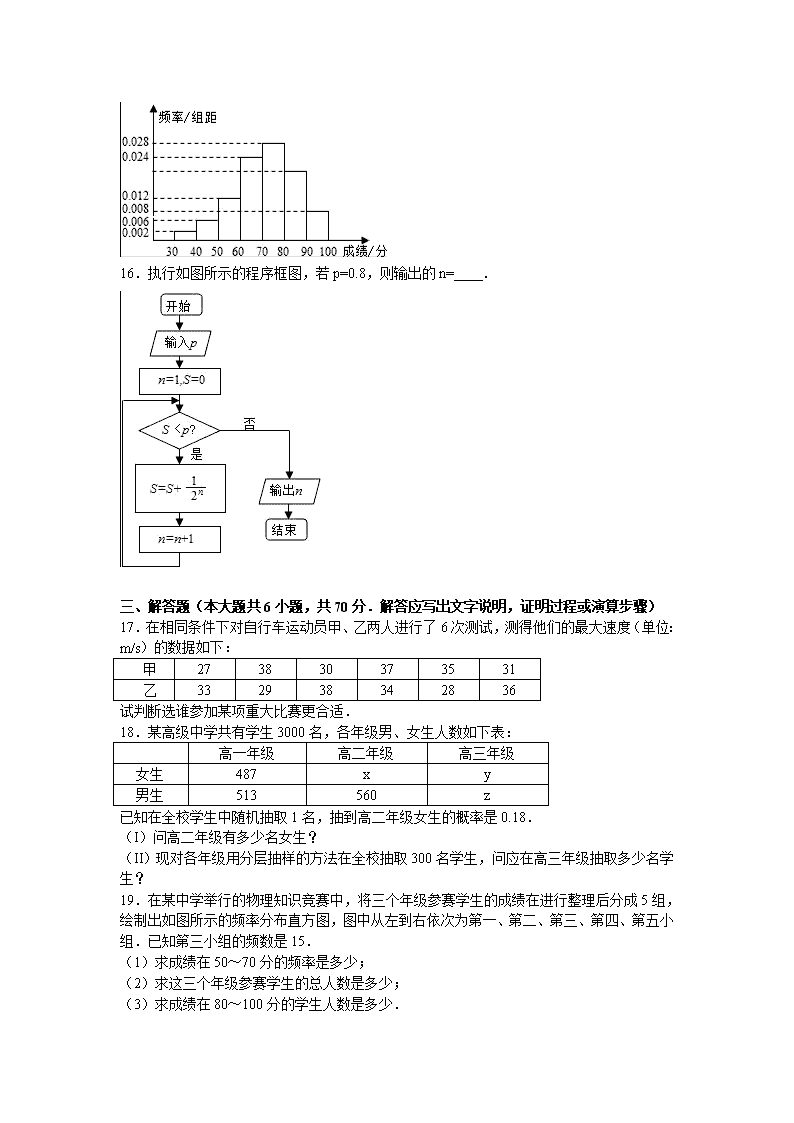
‎2016-2017学年江西省抚州市崇仁二中高二（上）第一次月考数学试卷（文科）‎ ‎　‎ 一.选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．为了调查全国人口的寿命，抽查了十一个省（市）的2500名城镇居民．这2500名城镇居民的寿命的全体是（　　）‎ A．总体 B．个体 C．样本 D．样本容量 ‎2．下列给出的赋值语句中正确的是（　　）‎ A．4=M B．M=﹣M C．B=A=3 D．X=Y=0‎ ‎3．某班的60名同学已编号1，2，3，…，60，为了解该班同学的作业情况，老师收取了号码能被5整除的12名同学的作业本，这里运用的抽样方法是（　　）‎ A．简单随机抽样法 B．系统抽样法 C．分层抽样法 D．抽签法 ‎4．已知x、y的取值如下表从所得的散点图分析，y与x线性相关，且=0.95x+a，则a=（　　） ‎ x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ A．2.1 B．2.2 C．2.4 D．2.6‎ ‎5．某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=（　　）‎ A．9 B．10 C．12 D．13‎ ‎6．直线4x﹣3y﹣2=0与圆（x﹣3）2+（y+5）2=36的位置关系为（　　）‎ A．相交 B．相切 C．相离 D．不确定 ‎7．给出以下四个问题：‎ ‎①输入一个正数x，求它的常用对数值； ‎ ‎②求面积为6的正方形的周长；‎ ‎③求三个数a，b，c中的最大数；‎ ‎④求函数的函数值．‎ 其中不需要用条件语句来描述其算法的有 （　　）‎ A．1个 B．2个 C．3个 D．4个 ‎8．如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图（两图都不完整），则下列结论中错误的是（　　）‎ A．该班总人数为50人 B．步行人数为30人 C．骑车人数占总人数的20%‎ D．乘车人数是骑车人数的2.5倍 ‎9．期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M：N为（　　）‎ A． B．1 C． D．2‎ ‎10．如图的程序框图表示的算法的功能是（　　）‎ A．计算小于100的奇数的连乘积 B．计算从1开始的连续奇数的连乘积 C．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数 D．计算1×3×5×…×n≥100时的最小的n值．‎ ‎11．在样本的频率分布直方图中，共有11个小长方形，若中间一个长方形的面积等于其他十个小长方形面积的和的，且样本容量是160，则中间一组的频数为（　　）‎ A．32 B．0.2 C．40 D．0.25‎ ‎12．若圆x2+y2﹣2x+4y+1=0上至少有两个点到直线2x+y﹣c=0的距离等于1，则实数c的取值范围为（　　）‎ A． B． C． D．‎ ‎　‎ 二.填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）‎ ‎13．某样本数据的茎叶图如图所示，若该组数据的中位数为85，平均数为85.5，则x+y=　　‎ ‎14．已知直线l1：ax+（3﹣a）y+1=0，l2：x﹣2y=0．若l1⊥l2，则实数a的值为　　．‎ ‎15．某小学为了解学生数学课程的学习情况，在3000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图（如图）．根据频率分布直方图3000名学生在该次数学考试中成绩小于60分的学生数是　　．‎ ‎16．执行如图所示的程序框图，若p=0.8，则输出的n=　　．‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）‎ ‎17．在相同条件下对自行车运动员甲、乙两人进行了6次测试，测得他们的最大速度（单位：m/s）的数据如下：‎ ‎ 甲 ‎27‎ ‎38‎ ‎30‎ ‎37‎ ‎35‎ ‎31‎ ‎ 乙 ‎33‎ ‎29‎ ‎38‎ ‎34‎ ‎28‎ ‎36‎ 试判断选谁参加某项重大比赛更合适．‎ ‎18．某高级中学共有学生3000名，各年级男、女生人数如下表：‎ 高一年级 高二年级 高三年级 女生 ‎487‎ x y 男生 ‎513‎ ‎560‎ z 已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．‎ ‎（I）问高二年级有多少名女生？‎ ‎（II）现对各年级用分层抽样的方法在全校抽取300名学生，问应在高三年级抽取多少名学生？‎ ‎19．在某中学举行的物理知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．‎ ‎（1）求成绩在50～70分的频率是多少；‎ ‎（2）求这三个年级参赛学生的总人数是多少；‎ ‎（3）求成绩在80～100分的学生人数是多少．‎ ‎20．某个服装店经营某种服装，在某周内获纯利润y（元）与该周每天销售这种服装件数x之间的一组数据关系见下表：‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ y ‎66‎ ‎69‎ ‎73‎ ‎81‎ ‎89‎ ‎90‎ ‎91‎ 已知： =280， xiyi=3 487．‎ ‎（1）求，；‎ ‎（2）画出散点图；‎ ‎（3）求纯利润y与每天销售件数x之间的回归直线方程．‎ ‎21．按如图所示的程序框图操作：‎ ‎（Ⅰ）写出输出的数所组成的数集．若将输出的数按照输出的顺序从前往后依次排列，则得到数列{an}，请写出数列{an}的通项公式；‎ ‎（Ⅱ）如何变更A框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{2n}的前7项？‎ ‎（Ⅲ）如何变更B框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项？‎ ‎22．已知点P为圆C1：（x﹣3）2+（y﹣4）2=4上的动点 ‎（1）若点Q为直线l：x+y﹣1=0上动点，求|PQ|的最小值与最大值；‎ ‎（2）若M为圆C2：（x+1）2+（y﹣1）2=4上动点，求|PM|的最大值和最小值．‎ ‎　‎ ‎2016-2017学年江西省抚州市崇仁二中高二（上）第一次月考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一.选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1．为了调查全国人口的寿命，抽查了十一个省（市）的2500名城镇居民．这2500名城镇居民的寿命的全体是（　　）‎ A．总体 B．个体 C．样本 D．样本容量 ‎【考点】用样本的频率分布估计总体分布．‎ ‎【分析】根据总体、个体、样本、样本容量的定义，可得结论．‎ ‎【解答】解：由题意可得，这2500名城镇居民的寿命的全体是样本，‎ 故选C．‎ ‎　‎ ‎2．下列给出的赋值语句中正确的是（　　）‎ A．4=M B．M=﹣M C．B=A=3 D．X=Y=0‎ ‎【考点】赋值语句．‎ ‎【分析】根据赋值语句的一般格式是：变量=表达式，赋值语句的左边只能是变量名称而不能是表达式，右边可以是数也可以是表达式，左右两边不能互换，只有B选项符合要求．‎ ‎【解答】解：根据赋值语句的一般格式是：变量=表达式，赋值语句的左边只能是变量名称而不能是表达式，‎ 右边可以是数也可以是表达式，左右两边不能互换，‎ A中，4=M，赋值符号左边不是变量，故A不正确；‎ C中，A=B=3，赋值语句不能连续赋值，故C不正确；‎ D中，X=Y=0，赋值语句不能连续赋值，故D不正确；‎ 故选：B．‎ ‎　‎ ‎3．某班的60名同学已编号1，2，3，…，60，为了解该班同学的作业情况，老师收取了号码能被5整除的12名同学的作业本，这里运用的抽样方法是（　　）‎ A．简单随机抽样法 B．系统抽样法 C．分层抽样法 D．抽签法 ‎【考点】系统抽样方法．‎ ‎【分析】根据系统抽样的定义进行判断即可．‎ ‎【解答】解：号码能被5整除的12名同学的间距相同，都是5，符合系统抽样的定义，‎ 故该抽样方法是系统抽样，‎ 故选：B ‎　‎ ‎4．已知x、y的取值如下表从所得的散点图分析，y与x线性相关，且=0.95x+a，则a=（　　） ‎ x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ A．2.1 B．2.2 C．2.4 D．2.6‎ ‎【考点】线性回归方程．‎ ‎【分析】本题考查的知识点是线性回归直线的性质，由线性回归直线方程中系数的求法，我们可知在回归直线上，满足回归直线的方程，我们根据已知表中数据计算出，再将点的坐标代入回归直线方程，即可求出对应的a值．‎ ‎【解答】解：点在回归直线上，‎ 计算得；‎ 代入得a=2.6；‎ 故选D．‎ ‎　‎ ‎5．某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=（　　）‎ A．9 B．10 C．12 D．13‎ ‎【考点】分层抽样方法．‎ ‎【分析】甲、乙、丙三个车间生产的产品数量的比依次为6：4：3，求出丙车间生产产品所占的比例，从而求出n的值．‎ ‎【解答】解：∵甲、乙、丙三个车间生产的产品件数分别是120，80，60，‎ ‎∴甲、乙、丙三个车间生产的产品数量的比依次为6：4：3，‎ 丙车间生产产品所占的比例，‎ 因为样本中丙车间生产产品有3件，占总产品的，‎ 所以样本容量n=3÷=13．‎ 故选D．‎ ‎　‎ ‎6．直线4x﹣3y﹣2=0与圆（x﹣3）2+（y+5）2=36的位置关系为（　　）‎ A．相交 B．相切 C．相离 D．不确定 ‎【考点】直线与圆的位置关系．‎ ‎【分析】求出圆心到直线的距离与圆的半径比较，可得直线和圆的位置关系．‎ ‎【解答】解：由于圆（x﹣3）2+（y+5）2=36的圆心为（3，﹣5）、半径为6，‎ 求得圆心（3，﹣5）到直线4x﹣3y﹣2=0的距离为=5，小于半径6，‎ 故直线和圆相交．‎ 故选：A．‎ ‎　‎ ‎7．给出以下四个问题：‎ ‎①输入一个正数x，求它的常用对数值； ‎ ‎②求面积为6的正方形的周长；‎ ‎③求三个数a，b，c中的最大数；‎ ‎④求函数的函数值．‎ 其中不需要用条件语句来描述其算法的有 （　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】条件语句；设计程序框图解决实际问题．‎ ‎【分析】对于选项①，②值，代入相应的公式求即可，对于选项③，④值域代入相应的公式时需要分类讨论，故要用到条件语句来描述其算法．‎ ‎【解答】解：对于①输入一个正数x，求它的常用对数值，代入lgx求即可；‎ 对于②，求面积为6的正方形的周长，代入a2求即可；‎ 对于③，求三个数a，b，c中的最大数，必须先进行大小比较，要用条件语句；‎ 对于④，求函数的函数值，必须对所给的x进行条件判断，也要用条件语句．‎ 其中不需要用条件语句来描述其算法的有2个．‎ 故选B．‎ ‎　‎ ‎8．如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图（两图都不完整），则下列结论中错误的是（　　）‎ A．该班总人数为50人 B．步行人数为30人 C．骑车人数占总人数的20%‎ D．乘车人数是骑车人数的2.5倍 ‎【考点】频率分布直方图．‎ ‎【分析】根据条形图和扇形图，对四个选项中的命题进行分析、判断即可．‎ ‎【解答】解：根据条形图和扇形图得出该班全体同学总数为25÷50%=50，∴A正确；‎ 根据选项A知该班外出时步行人数为50×30%=15，∴B错误；‎ 根据扇形图知骑车人数占总人数的20%，∴C正确；‎ 根据题意乘车人数是25，骑车人数是10，乘车人数是骑车人数的2.5倍，∴D正确．‎ 故选：B．‎ ‎　‎ ‎9．期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N，那么M：N为（　　）‎ A． B．1 C． D．2‎ ‎【考点】众数、中位数、平均数．‎ ‎【分析】全班40个人数学成绩的平均分为M，把M当成一个同学的分数，则班中有41名同学，可以算出41名同学的总分，再除以41，得到平均值，结果同原来40人的平均数相同．‎ ‎【解答】解：∵全班40个人数学成绩的平均分为M，‎ 把M当成一个同学的分数，‎ 则班中有41名同学共为41M，‎ ‎∴41人的平均分=，‎ 故选B ‎　‎ ‎10．如图的程序框图表示的算法的功能是（　　）‎ A．计算小于100的奇数的连乘积 B．计算从1开始的连续奇数的连乘积 C．从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数 D．计算1×3×5×…×n≥100时的最小的n值．‎ ‎【考点】程序框图．‎ ‎【分析】写出经过几次循环得到的结果，得到求的s的形式，判断出框图的功能．‎ ‎【解答】解：模拟程序的运行，可得 s=1，i=3‎ s=1×3，‎ 不满足条件s≥100，执行循环体，i=5，s=1×3×5，‎ 不满足条件s≥100，执行循环体，i=7，s=1×3×5×7，‎ 不满足条件s≥100，执行循环体，i=9，s=1×3×5×7×9，‎ ‎…‎ s=1×3×5×7×…×i≥100，‎ 满足条件s≥100，退出循环，输出i的值，‎ 该程序框图表示算法的功能是求从1开始的连续奇数的连乘积，当乘积大于100时，计算奇数的个数，‎ 故选：C．‎ ‎　‎ ‎11．在样本的频率分布直方图中，共有11个小长方形，若中间一个长方形的面积等于其他十个小长方形面积的和的，且样本容量是160，则中间一组的频数为（　　）‎ A．32 B．0.2 C．40 D．0.25‎ ‎【考点】频率分布直方图．‎ ‎【分析】据已知求出频率分布直方图的总面积；求出中间一组的频率；利用频率公式求出中间一组的频数．‎ ‎【解答】解：设间一个长方形的面积S则其他十个小长方形面积的和为4S，所以频率分布直方图的总面积为5S 所以中间一组的频率为 所以中间一组的频数为160×0.2=32‎ 故选A ‎　‎ ‎12．若圆x2+y2﹣2x+4y+1=0上至少有两个点到直线2x+y﹣c=0的距离等于1，则实数c的取值范围为（　　）‎ A． B． C． D．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】把圆的方程化为标准方程后，找出圆心坐标和圆的半径，用点到直线的距离公式表示出圆心到已知直线的距离d，画出图象，根据图象和题意列出关于d的不等式，求出不等式的解集即可得到c的取值范围．‎ ‎【解答】解：把圆的方程化为标准方程得：（x﹣1）2+（y+2）2=4，‎ 得到圆心坐标为（1，﹣2），半径r=2，‎ 根据题意画出图象，如图所示：‎ 因为圆心到直线2x+y﹣c=0的距离d=，‎ 根据图象可知：当0≤d＜3时，‎ 圆上至少有两个点到直线2x+y+c=0距离等于1，‎ 即0≤＜3，‎ 解得，＜c＜3，‎ 则满足题意的c的取值范围是（﹣3，3），‎ 故选：C．‎ ‎　‎ 二.填空题（本大题共4小题，每小题5分，共20分，把答案填在题中横线上）‎ ‎13．某样本数据的茎叶图如图所示，若该组数据的中位数为85，平均数为85.5，则x+y=　13　‎ ‎【考点】茎叶图．‎ ‎【分析】根据中位数的概念，求出x的值，再根据平均数的概念，求出y的值，即可得出结论 ‎【解答】解：根据题意，得；‎ 当该组数据的中位数为85时，（84+80+x）=85，‎ 解得x=6；‎ 所以该组数据的平均数为（73+79+84+84+84+86+87+88+93+90+y）=85.5，‎ 解得y=7；‎ 所以x+y=13．‎ 故答案为：13‎ ‎　‎ ‎14．已知直线l1：ax+（3﹣a）y+1=0，l2：x﹣2y=0．若l1⊥l2，则实数a的值为　2　．‎ ‎【考点】直线的一般式方程与直线的垂直关系．‎ ‎【分析】求出直线l2的斜率，根据l1⊥l2，得到l1的斜率，得到关于a的方程，求出a的值即可．‎ ‎【解答】解：已知直线l1：ax+（3﹣a）y+1=0，l2：x﹣2y=0，‎ 直线l2的斜率是，‎ 若l1⊥l2，则l1的斜率是﹣2，‎ 故=﹣2，解得：a=2，‎ 故答案为：2．‎ ‎　‎ ‎15．某小学为了解学生数学课程的学习情况，在3000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图（如图）．根据频率分布直方图3000名学生在该次数学考试中成绩小于60分的学生数是　600　．‎ ‎【考点】频率分布直方图．‎ ‎【分析】首先计算成绩小于60 的三个小矩形的面积之和，即成绩小于60 的学生的频率，再乘以3000即可．‎ ‎【解答】解：由频率分布直方图成绩小于60 的学生的频率为10（0.002+0.006+0.012）=0.2，‎ 所以成绩小于60分的学生数是3000×0，2=600‎ 故答案为：600‎ ‎　‎ ‎16．执行如图所示的程序框图，若p=0.8，则输出的n=　4　．‎ ‎【考点】程序框图．‎ ‎【分析】根据流程图所示的顺序，逐框分析程序中各变量、各语句的作用可知：该程序的作用是判断S=＞0.8时，n+1的值．‎ ‎【解答】解：根据流程图所示的顺序，‎ 该程序的作用是判断S=＞0.8时，n+1的值．‎ 当n=2时，‎ 当n=3时，，‎ 此时n+1=4．‎ 故答案为：4‎ ‎　‎ 三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤）‎ ‎17．在相同条件下对自行车运动员甲、乙两人进行了6次测试，测得他们的最大速度（单位：m/s）的数据如下：‎ ‎ 甲 ‎27‎ ‎38‎ ‎30‎ ‎37‎ ‎35‎ ‎31‎ ‎ 乙 ‎33‎ ‎29‎ ‎38‎ ‎34‎ ‎28‎ ‎36‎ 试判断选谁参加某项重大比赛更合适．‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】先做出甲和乙的速度的平均数，甲和乙的速度的平均数相同，需要再比较两组数据的方差，选方差较小运动员参加比赛比较好．‎ ‎【解答】解：平均速度 =（27+38+30+37+35+31）=33；‎ ‎=（33+29+38+34+28+36）=33．‎ s甲2= [（﹣6）2+52+（﹣3）2+42+22+（﹣2）2]=；‎ s乙2= [（﹣4）2+52+12+（﹣5）2+32]=．‎ ‎∵=，s甲2＞s乙2，‎ ‎∴乙的成绩比甲稳定．‎ 应选乙参加比赛更合适．‎ ‎　‎ ‎18．某高级中学共有学生3000名，各年级男、女生人数如下表：‎ 高一年级 高二年级 高三年级 女生 ‎487‎ x y 男生 ‎513‎ ‎560‎ z 已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.18．‎ ‎（I）问高二年级有多少名女生？‎ ‎（II）现对各年级用分层抽样的方法在全校抽取300名学生，问应在高三年级抽取多少名学生？‎ ‎【考点】分层抽样方法；简单随机抽样．‎ ‎【分析】（1）先根据抽到高二年级女生的概率=0.18得x=540．从而得出高二年级有多少名女生；‎ ‎（2）根据表格可知，高三年级人数为：y+z=3000﹣=900．全校要抽取300人，做出每个个体被抽到的概率，做出高三被抽到的人数．‎ ‎【解答】解：（1）由=0.18得x=540．所以高二年级有540名女生．…‎ ‎（2）高三年级人数为：y+z=3000﹣=900．‎ ‎∴×300=90（人）．故应在高三年级抽取90名学生．…‎ ‎　‎ ‎19．在某中学举行的物理知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组．已知第三小组的频数是15．‎ ‎（1）求成绩在50～70分的频率是多少；‎ ‎（2）求这三个年级参赛学生的总人数是多少；‎ ‎（3）求成绩在80～100分的学生人数是多少．‎ ‎【考点】频率分布直方图．‎ ‎【分析】（1）根据频率分布直方图的矩形面积表示频率，求出成绩在50﹣70分的矩形面积，即为所求；‎ ‎（2）求出第三组的频率，然后根据三个年级参赛学生的总人数=，可求出所求；‎ ‎（3）先求出成绩在80﹣100分的频率，然后利用频数=总数×频率可求出成绩在80﹣100分的学生人数．‎ ‎【解答】解：（1）成绩在50﹣70分的频率为：0.03×10+0.04×10=0.7‎ ‎（2）第三小组的频率为：0.015×10=0.15‎ 这三个年级参赛学生的总人数（总数=）为： =100（人）‎ ‎（3）成绩在80﹣100分的频率为：0.01×10+0.005×10=0.15‎ 则成绩在80﹣100分的人数为：100×0.15=15（人） …．‎ ‎　‎ ‎20．某个服装店经营某种服装，在某周内获纯利润y（元）与该周每天销售这种服装件数x之间的一组数据关系见下表：‎ x ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ y ‎66‎ ‎69‎ ‎73‎ ‎81‎ ‎89‎ ‎90‎ ‎91‎ 已知： =280， xiyi=3 487．‎ ‎（1）求，；‎ ‎（2）画出散点图；‎ ‎（3）求纯利润y与每天销售件数x之间的回归直线方程．‎ ‎【考点】线性回归方程．‎ ‎【分析】（1）利用平均数公式计算即得．‎ ‎（2）把所给的7对数据写成对应的点的坐标，在坐标系中描出来，得到散点图．‎ ‎（3）作出利用最小二乘法来求线性回归方程的系数的量，求出横标和纵标的平均数，求出系数，再求出a的值，即可求出回归方程．‎ ‎【解答】【解】（1）==6（件），==≈79.86（元）．‎ ‎（2）散点图如下：‎ ‎（3）由散点图知，y与x有线性相关关系．设回归直线方程为y=bx+a．‎ b==4.75，a=﹣6×4.75≈51.36．‎ 故回归直线方程为y=4.75x+51.36．‎ ‎　‎ ‎21．按如图所示的程序框图操作：‎ ‎（Ⅰ）写出输出的数所组成的数集．若将输出的数按照输出的顺序从前往后依次排列，则得到数列{an}，请写出数列{an}的通项公式；‎ ‎（Ⅱ）如何变更A框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{2n}的前7项？‎ ‎（Ⅲ）如何变更B框内的赋值语句，使得根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项？‎ ‎【考点】等差数列的前n项和；循环结构．‎ ‎【分析】（Ⅰ）由程序框图可知，本题求一个数列的前7项，且这一数列首项为1，后面每一项比前面项多2，所以可得输出的数组成的集合，并且此数列{an}恰为首项为1，公差为2的等差数列，再用等差数列通项公式即可求出数列{an}的通项公式 ‎（Ⅱ）要想使根据这个程序框图所输出的数恰好是数列{2n}的前7项，则前7项应为2，4，6，8，10，12，14，所以只需．将A框内的语句改为“a=2”即可．‎ ‎（Ⅲ）要想使根据这个程序框图所输出的数恰好是数列{3n﹣2}的前7项，则前7项应为1，4，7，10，13，16，19．只需将B框内的语句改为“a=a+3”即可．‎ ‎【解答】解：（Ⅰ）输出的数组成的集合为{1，3，5，7，9，11，13}；‎ 数列{an}的通项公式为an=2n﹣1（n∈N*，且n≤7）．‎ ‎（Ⅱ）将A框内的语句改为“a=2”即可．‎ ‎（Ⅲ）将B框内的语句改为“a=a+3”即可．‎ ‎　‎ ‎22．已知点P为圆C1：（x﹣3）2+（y﹣4）2=4上的动点 ‎（1）若点Q为直线l：x+y﹣1=0上动点，求|PQ|的最小值与最大值；‎ ‎（2）若M为圆C2：（x+1）2+（y﹣1）2=4上动点，求|PM|的最大值和最小值．‎ ‎【考点】圆方程的综合应用．‎ ‎【分析】（1）求出圆心C1：（3，4），半径r1=2，及圆心到直线的距离，由图形观察即可得到最值；‎ ‎（2）求出圆心C2为（﹣1，1），半径为r2=2，求出圆心的距离，判断两圆的位置关系，通过图形观察即可得到所求最值．‎ ‎【解答】解：（1）圆C1：（x﹣3）2+（y﹣4）2=4的圆心C1：（3，4），半径r1=2，‎ 圆心C1到直线x+y﹣1=0的距离为d==3＞2，‎ 即有直线和圆相离，即有|PQ|的最小值为3﹣2，无最大值；‎ ‎（2）圆C2：（x+1）2+（y﹣1）2=4的圆心C2为（﹣1，1），半径为r2=2，‎ 由|C1C2|==5＞r1+r2=4，即有两圆相离，‎ 即有|PM|的最大值为5+4=9，最小值为5﹣4=1．‎ ‎　‎ ‎2017年1月10日