高中数学北师大版新教材必修一同步课件：阶段提升课 第五课　统计

高中数学北师大版新教材必修一同步课件：阶段提升课 第五课　统计

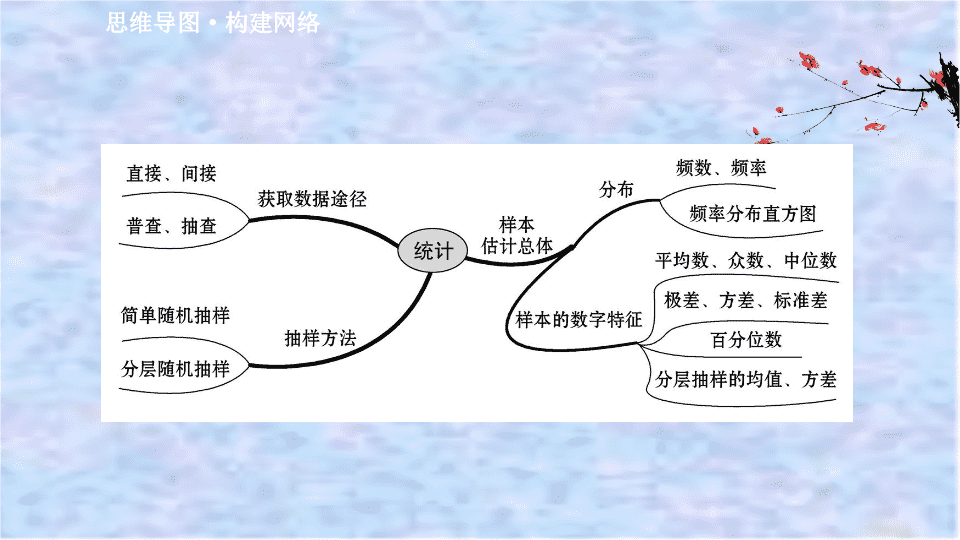
阶段提升课 第五课　统　　计 思维导图 · 构建网络 考点整合 · 素养提升 题组训练一　抽样的基本方法  1. 某公司生产 A,B,C 三种不同型号的轿车 , 其产量之比为 2∶3∶4, 为检验该公司 的产品质量 , 用分层随机抽样的方法抽取一个容量为 n 的样本 , 若样本中 A 种型号 的轿车比 B 种型号的轿车少 8 辆 , 则 n= ( 　　 ) A.96 　　　 B.72 　　　 C.48 　　　 D.36 【 解析 】 选 B. 由题意得 n- n=8, 所以 n=72. 2. 下列抽取样本时运用了哪种抽样方法 ? 并说明原因 . 设一个总体中的个体数 N=345, 要抽取一个容量为 n=15 的样本 , 现采用如下方法 : 从随机数表中任意选取三列构成三位数字号码 , 从中依次取出不同的三位数字号码 , 当数在 001 ～ 345 之间时 , 该号码抽入样本 ; 当数在 401 ～ 745 之间时 , 则该数减去 400 的号码抽入样本中 , 其余的 000,346 ～ 400,746 ～ 999 的号码都不要 ; 当某号码已抽入样本中 , 而再次遇到该号码被抽入样本时 , 只算一次 . 【 解析 】 运用了简单随机抽样中的随机数法 . 简单随机抽样的要求是给个体编号 , 逐个不放回抽取 , 操作的个体数量不宜太多 , 每个个体被抽取的机会均等 , 只有符合这些特点才是简单随机抽样 . 本题虽然取数时 , 设计了特别的规则 , 但是从随机数表中任意取数符合简单随机抽样的特点 , 所以本题运用了简单随机抽样中的随机数法 . 【 方法技巧 】 抽样方法的特点及选取规则 简单随机抽样和比例分配的分层随机抽样的共同特点是在抽样过程中每个个体被抽取的机会相等 , 体现了这些抽样方法的客观性和公平性 . 当总体中的个体数较少时 , 常采用简单随机抽样 ; 当已知总体由差异明显的几部分组成时 , 常采用分层随机抽样 . 在进行分层随机抽样时要用到简单随机抽样方法 . 题组训练二　 用样本的频率分布估计总体分布  1. 有一个容量为 66 的样本 , 数据的分组及各组的频数如下 : [11.5,15.5) 2,[15.5,19.5) 4,[19.5,23.5) 9, [23.5,27.5) 18,[27.5,31.5) 11,[31.5,35.5) 12, [35.5,39.5) 7,[39.5,43.5] 3, 则总体中大于或等于 31.5 的数据所占的比例为 ( 　　 ) 【 解析 】 选 B. 由题意知 , 样本量为 66, 而落在 [31.5,43.5] 内的样本个数为 12+7+3=22, 故总体中大于或等于 31.5 的数据约占 2. 对某校高三年级学生参加社区服务的次数进行统计 , 随机抽取 M 名学生 , 得到这 M 名学生参加社区服务的次数 , 根据此数据作出了频率分布表和频率分布直方图 , 如图所示 : 分组 频数 频率 [10,15) 10 0.25 [15,20) 24 n [20,25) m p [25,30] 2 0.05 合计 M 1 (1) 求表中 M,p 及图中 a 的值 ; (2) 若该校高三学生有 240 人 , 试估计该校高三学生参加社区服务的次数在区间 [10,15) 内的人数 . 【 解析 】 (1) 由分组 [10,15) 的频数是 10, 频率是 0.25, 知 =0.25, 解得 M=40. 因为频数之和为 40, 所以 10+24+m+2=40, 得 m=4,p= =0.10. 因为 a 是对应分组 [15,20) 的频率与组距的商 , 所以 a= =0.12. (2) 因为该校高三学生有 240 人 , 分组 [10,15) 的频率是 0.25, 所以估计该校高三 学生参加社区服务的次数在区间 [10,15) 内的人数为 240×0.25=60. 【 方法技巧 】 与频率分布直方图有关问题的常见类型及解题策略 (1) 已知频率分布直方图中的部分数据 , 求其他数据 , 可根据频率分布直方图中的数据求出样本与整体的关系 , 利用频率和等于 1 可求出其他数据 . (2) 已知频率分布直方图 , 求某种范围内的数据 , 可利用图形及某范围结合求解 . 题组训练三　 用样本估计总体的数字特征  1.(2019· 全国卷 Ⅱ) 演讲比赛共有 9 位评委分别给出某选手的原始评分 , 评定该选手的成绩时 , 从 9 个原始评分中去掉 1 个最高分、 1 个最低分 , 得到 7 个有效评分 .7 个有效评分与 9 个原始评分相比 , 不变的数字特征是 ( 　　 ) A. 中位数 B. 平均数 C. 方差 D. 极差 【 解析 】 选 A. 由于去掉 1 个最高分、 1 个最低分 , 不影响中间的数值 , 故中位数不变 . 2. 某工厂甲、乙两个车间包装同一种产品 , 在自动包装传送带上每隔一小时抽一包产品 , 称其质量 ( 单位 : 克 ) 是否合格 , 分别记录抽查数据 , 获得质量数据如下 . 甲 :107,111,111,113,114,122; 乙 :108,109,110,112,115,124. (1) 写出甲的众数和乙的中位数 ; (2) 根据样本数据 , 计算甲、乙两个车间产品质量的均值与方差 , 并说明哪个车间的产品的质量相对稳定 . 【 解析 】 (1) 甲的众数是 111, 乙的中位数是 111. (2) 设甲、乙两个车间产品质量的均值分别为 方差分别为 [(122-113) 2 +(114-113) 2 +(113-113) 2 +(111-113) 2 +(111-113) 2 +(107- 113) 2 ]=21, [(124-113) 2 +(110-113) 2 +(112-113) 2 +(115-113) 2 +(108-113) 2 +(109- 113) 2 ]≈29.33, 由于 所以甲车间的产品的质量相对稳定 . 【 方法技巧 】 利用样本数据的数字特征估计总体问题 (1) 平均数、众数、中位数都是描述一组数据的特点 , 但描述的含义不同 . (2) 标准差、方差都是描述一组数据波动情况的量 , 越小就表示越稳定 . 题组训练四　 样本的百分位数  1. 某次能力测试中 ,10 人的成绩统计如表 , 则这 10 人成绩的平均数为 _______, 20% 分位数为 _______.  分数 5 4 3 2 1 人数 ( 单位 : 人 ) 3 1 2 1 3 【 解析 】 这 10 人成绩的平均数为 ×(5×3+4×1+3×2+2×1+1×3)= × (15+4+6+2+3)= ×30=3. 因为 10×20%=2, 所以这 10 人成绩的 20% 分位数为 =1. 答案 : 3 　 1 2. 一家保险公司决定对推销员实行目标管理 , 即给推销员确定一个具体的销售目标 . 确定的销售目标是否合适 , 直接影响到公司的经济效益 . 如果目标定得过高 , 多数推销员完不成任务 , 会使推销员失去信心 ; 如果目标定得太低 , 将不利于挖掘推销员的工作潜力 . 下面一组数据是部分推销员的月销售额 ( 单位 : 千元 ). 19.58 16.11 16.45 20.45 20.24 21.66 22.45 18.22 12.34 19.35 20.55 17.45 18.78 17.96 19.91 18.12 14.65 14.78 16.78 18.78 18.29 18.51 17.86 19.58 19.21 18.55 16.34 15.54 17.55 14.89 18.94 17.43 17.14 18.02 19.98 17.88 17.32 19.35 15.45 19.58 13.45 21.34 14.00 18.42 23.00 17.52 18.51 17.16 24.56 25.14 请根据这组样本数据提出使 65% 的职工能够完成销售指标的建议 . 【 解析 】 将这 50 个样本数据按从小到大排序 , 可得 12.34 13.45 14.00 14.65 14.78 14.89 15.45 15.54 16.11 16.34 16.45 16.78 17.14 17.16 17.32 17.43 17.45 17.52 17.55 17.86 17.88 17.96 18.02 18.12 18.22 18.29 18.42 18.51 18.51 18.55 18.78 18.78 18.94 19.21 19.35 19.35 19.58 19.58 19.58 19.91 19.98 20.24 20.45 20.55 21.34 21.66 22.45 23.00 24.56 25.14 由 65% 的职工能够完成销售指标 , 那么 35% 的职工不能完成销售指标 . 由 50×(1-65%)=17.5 可知这组数据的 35% 分位数为 17.52. 故为使 65% 的职工能够完成销售指标 , 该保险公司可将月销售额定为 17.52 千元 . 【 方法技巧 】 计算一组 n 个数据的 p 分位数的一般步骤 第 1 步 , 按从小到大排列原始数据 . 第 2 步 , 计算 i=n×p. 第 3 步 , 若 i 不是整数 , 而大于 i 的比邻整数为 j, 则 p 分位数为第 j 项数据 ; 若 i 是整数 , 则 p 分位数为第 i 项与第 (i+1) 项数据的平均数 .