【数学】新疆阿勒泰地区2019-2020学年高二下学期期末考试试题(文)(解析版)
新疆阿勒泰地区2019-2020学年
高二下学期期末考试试题(文)
一选择题(每题5分,共60分)
1已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)=( )
A.{1,3,4} B.{3,4} C.{3} D.{4}
2命题“∀x∈R,x2≠x”的否定是( )
A.∀x∉R,x2≠x B.∀x∈R,x2=x
C.∃x∉R,x2≠x D.∃x∈R,x2=x
3复数z=的模为( )
A. B. C. D.2
4设a,b∈R,则“a+b>4”是“a>2且b>2”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
5函数f(x)=a3+5a2x2的导数f′(x)=( )
A.3a2+10ax2 B.3a2+10ax2+10a2x C.10a2x D.以上都不对
6(文1)直线l的参数方程为(t为参数),则直线l的斜率为( )
A.3 B. C.- D.-3
6(文2)方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
7(文1)在极坐标系中,极坐标化为直角坐标为( )
A.(1,1) B.(-1,1) C.(1,-1) D.(-1,-1)
7(文2)设双曲线-=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
A.4 B.3 C.1 D.2
8已知曲线y=-3lnx的一条切线的斜率为-,则切点的横坐标为
( )
A.3 B.2 C.1 D.
9设a=log37,b=21.1,c=0.83.1,则( )
A.b<a<c B.c<a<b C.c<b<a D.a<c<b
10.函数f(x)=x3-3x2+m在区间[-1,1]上的最大值是2,则常数m=( )
A.-2 B.0 C.2 D.4
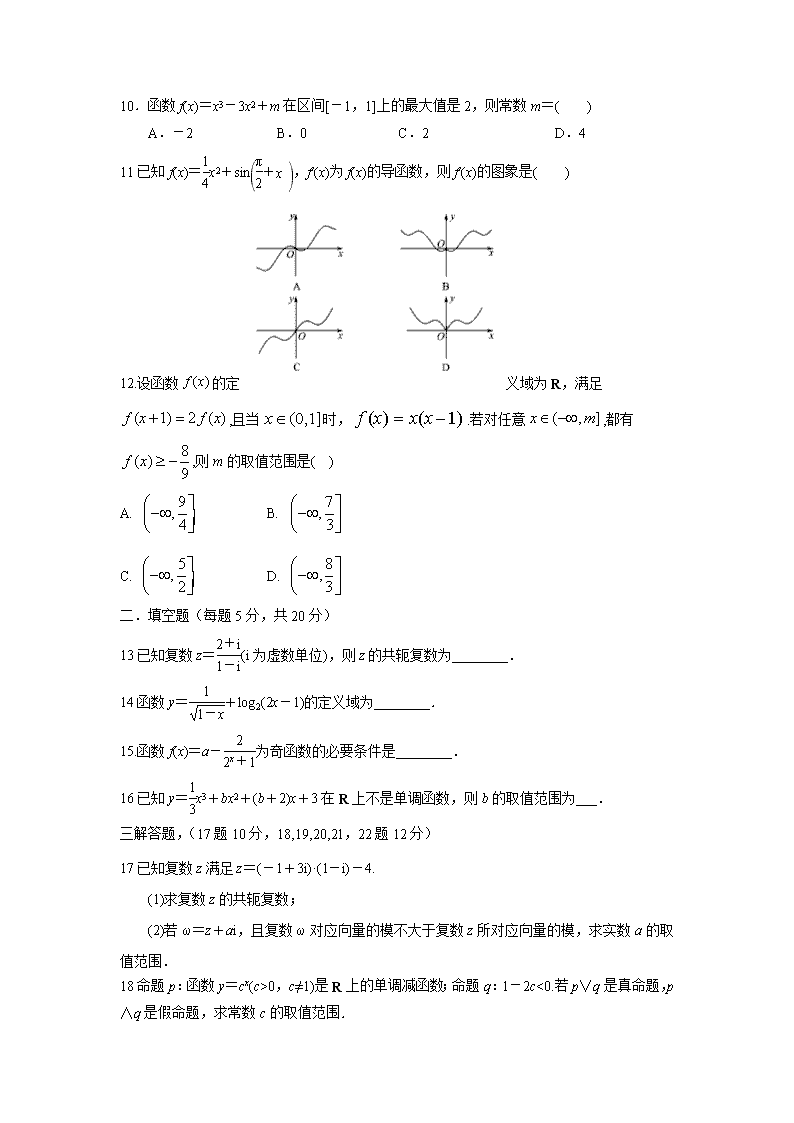
11已知f(x)=x2+sin,f′(x)为f(x)的导函数,则f′(x)的图象是( )
12.设函数的定义域为R,满足,且当时,.若对任意,都有,则m的取值范围是( )
A. B.
C. D.
二.填空题(每题5分,共20分)
13已知复数z=(i为虚数单位),则z的共轭复数为________.
14函数y=+log2(2x-1)的定义域为________.
15.函数f(x)=a-为奇函数的必要条件是________.
16已知y=x3+bx2+(b+2)x+3在R上不是单调函数,则b的取值范围为___.
三解答题,(17题10分,18,19,20,21,22题12分)
17已知复数z满足z=(-1+3i)·(1-i)-4.
(1)求复数z的共轭复数;
(2)若ω=z+ai,且复数ω对应向量的模不大于复数z所对应向量的模,求实数a的取值范围.
18命题p:函数y=cx(c>0,c≠1)是R上的单调减函数;命题q:1-2c<0.若p∨q是真命题,p∧q是假命题,求常数c的取值范围.
19已知函数f(x)=loga(1-x)+loga(x+3),其中0
b>0)的离心率e=,焦距是2.
(1)求椭圆的方程;
(2)若直线y=kx+2(k≠0)与椭圆交于C、D两点,|CD|=,求k的值.
22已知实数a>0,函数f(x)=a(x-2)2+2lnx.
(1)当a=1时,讨论函数f(x)的单调性;
(2)若f(x)在区间[1,4]上是增函数,求实数a的取值范围.
参考答案
一选择,每题5分,共60分
1已知全集U={1,2,3,4},集合A={1,2},B={2,3},则∁U(A∪B)=( D)
A.{1,3,4} B.{3,4} C.{3} D.{4}
解:∵A∪B={1,2,3},∴∁U(A∪B)={4}.故选D.
2命题“∀x∈R,x2≠x”的否定是(D )
A.∀x∉R,x2≠x B.∀x∈R,x2=x
C.∃x∉R,x2≠x D.∃x∈R,x2=x
解:全称命题的否定是特称命题.故选D
3复数z=的模为( B )
A. B. C. D.2
解析:z===--i,∴|z|= =,故选B.
4设a,b∈R,则“a+b>4”是“a>2且b>2”的(B )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
解:当a=5,b=0时,满足a+b>4,但a>2且b>2不成立,即充分性不成立;
若a>2且b>2,则必有a+b>4,即必要性成立.
因此,“a+b>4”是“a>2且b>2”的必要非充分条件.故选B.
5函数f(x)=a3+5a2x2的导数f′(x)=( C )
A.3a2+10ax2 B.3a2+10ax2+10a2x C.10a2x D.以上都不对
解:f′(x)=10a2x.故选C.
6(文1)直线l的参数方程为(t为参数),则直线l的斜率为( D )
A.3 B. C.- D.-3
解析:将直线l的方程化为普通方程为y-2=-3(x-1),所以直线l的斜率为-3,故选D.答案:D
6(文2).方程x2+ky2=2表示焦点在y轴上的椭圆,则k的取值范围是( D )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
解:将方程x2+ky2=2变形为+=1,根据椭圆的定义,要使焦点在y轴,只须
>2,解得00,即4b2-4(b+2)>0,∴b>2或b<-1,
∴b的取值范围是(-∞,-1)∪(2,+∞).
答案:(-∞,-1)∪(2,+∞)
三解答题,(17题10分,18,19,20,21,22题12分)
17已知复数z满足z=(-1+3i)·(1-i)-4.
(1)求复数z的共轭复数;
(2)若ω=z+ai,且复数ω对应向量的模不大于复数z所对应向量的模,求实数a的取值范围.
解:(1)z=-1+i+3i+3-4=-2+4i,所以复数z的共轭复数为-2-4i.。。。。4分
(2)ω=-2+(4+a)i,复数ω对应向量为(-2,4+a), 。。。。。。。。。。。6分
其模为=.
又复数z所对应向量为(-2,4),其模为2.由复数ω对应向量的模不大于复数z所对应向量的模得,20+8a+a2≤20,,,,,8分
a2+8a≤0,a(a+8)≤0,所以,实数a的取值范围是-8≤a≤0. ,,,,,,,,,10分
18命题p:函数y=cx(c>0,c≠1)是R上的单调减函数;命题q:1-2c<0.若p∨q是真命题,p∧q是假命题,求常数c的取值范围.
解:∵p∨q是真命题,p∧q是假命题,
∴p,q中一个是真命题,一个是假命题. ,,,,,,,,,,,2分
若p真q假,则有解得01.,,,,,,,,,,,,10分
综上可知,满足条件的c的取值范围是∪(1,+∞),,12分
19已知函数f(x)=loga(1-x)+loga(x+3),其中0b>0)的离心率e=,焦距是2.
(1)求椭圆的方程;
(2)若直线y=kx+2(k≠0)与椭圆交于C、D两点,|CD|=,求k的值.
解析:(1)由题意得2c=2,所以c2=2,又=,所以a2=3,b2=1,,,,3分
∴椭圆方程为+y2=1. 。。4分
(2)设C(x1,y1)、D(x2,y2),将y=kx+2带入+y2=1,
整理得(1+3k2)x2+12kx+9=0,
所以Δ=(12k)2-36(1+3k2)>0 。。。。。5分
。。。。。。。6分
又|CD|=,
y1-y2=k(x1-x2),
所以=, 。。。。。。。8分
又(x1-x2)2=(x1+x2)2-4x1x2=-, 。。。9分
代入上式,整理得7k4-12k2-27=0,即(7k2+9)(k2-3)=0,,,,,,,,,,,,,10分
解得k2=-(舍去)或k2=3,即k=±,
经验证,k=±能使①成立,故k=±. ,,,,,,,,,,12分
22已知实数a>0,函数f(x)=a(x-2)2+2lnx.
(1)当a=1时,讨论函数f(x)的单调性;
(2)若f(x)在区间[1,4]上是增函数,求实数a的取值范围.
解:(1)当a=1时,f(x)=x2-4x+4+2lnx,
f′(x)=2x-4+=,。。。。。。。。。。。。。。。2分
∵x>0,∴f′(x)≥0, 。。。。。。。。。。。。。。3分
∴f(x)在区间(0,+∞)上单调递增.。。。。。。。。。。。。。4分
(2)∵f′(x)=2ax-4a+=, 。。。。5分
又f(x)在区间[1,4]上是增函数
∴f′(x)=≥0对x∈[1,4]恒成立,,,,,,,,7分
即2ax2-4ax+2≥0对x∈[1,4]恒成立。。。。。。。。。。。。。8分
令g(x)=2ax2-4ax+2, 。。。。。。。。9分
则g(x)=2a(x-1)2+2-2a,。。。。。。。。。。。。。。。。。。。。。。10
∵a>0,∴g(x)在[1,4]上单调递增,.。。。。。。。。。。。。11分
只要使g(x)min=g(1)=2-2a≥0即可,∴0<a≤1.。。。12分