2017-2018学年云南省玉溪市民族中学高二上学期第一次阶段性考试数学试题

2017-2018学年云南省玉溪市民族中学高二上学期第一次阶段性考试数学试题

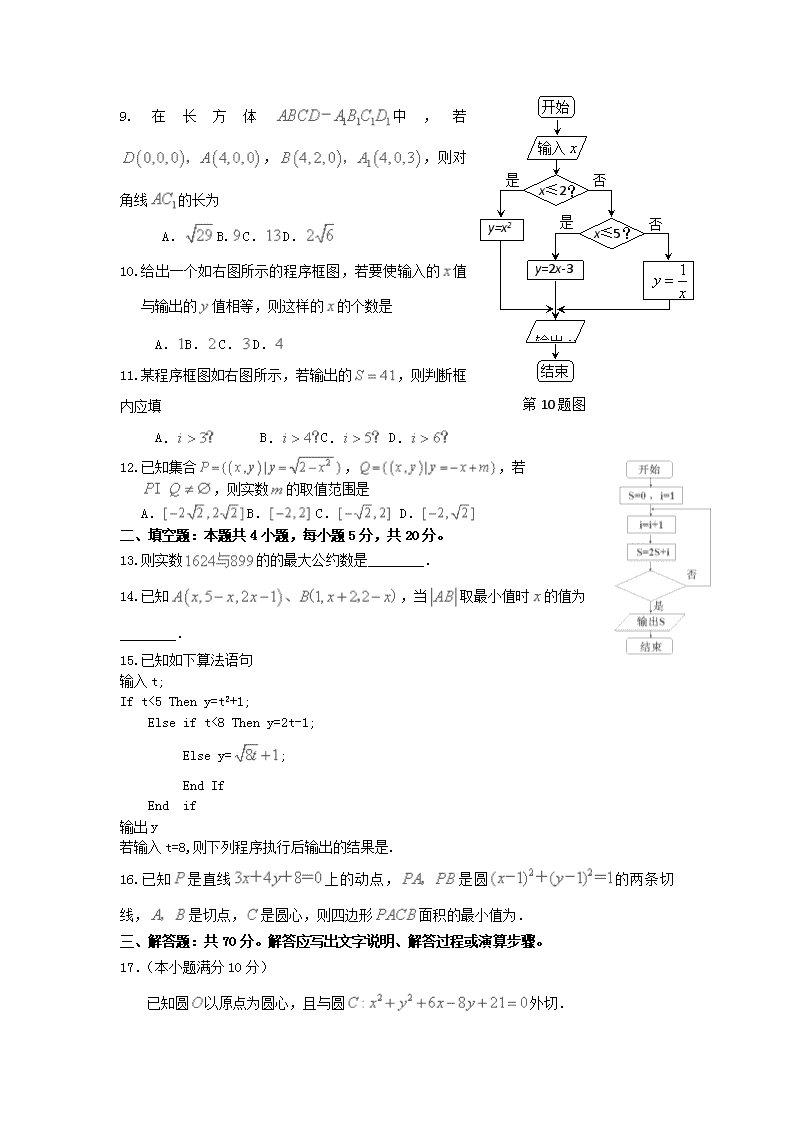
‎2017-2018学年云南省玉溪市民族中学高二上学期第一次阶段性考试数学试卷（文理同卷）‎ 命题教师：李燕祥 联系电话65032‎ 一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.在简单随机抽样中，某一个个体被抽中的可能性 A.与第几次抽样无关，第一次抽中的可能性要大些 B.与第几次抽样有关，最后一次抽中的可能性大些 C.与第几次抽样无关，每次抽中的可能性相等 D.与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样 ‎2.已知，则以线段为直径的圆的方程是 A．B．‎ C．D．‎ ‎3.执行右边的程序框图，若输入的的值为，则输出的值是 A． B．C． D．‎ ‎4.某防疫站对学生进行身体健康调查，欲采用分层抽样的办法抽取样本．某中学共有学生名，抽取了一个容量为的样本，已知样本中女生比男生少人，则该校共有女生 A．人B．人 C．人D．人 ‎5.直线与圆的位置关系 A．相交 B．相切C．相交且过圆心 D．相离 ‎6.某年级有名学生，随机编号为，现用系统抽样方法，从中抽出人，若号被抽到了，则下列编号也被抽到的是 A．B．C．D．‎ ‎7.两个二进制数与的和用十进制数表示为 A． B． C． D．‎ ‎8.如图，在正方体中，棱长为，，则点的坐标为 A．B．‎ C．D．‎ y=2x-3‎ 开始 输入 x≤2？‎ x≤5？‎ y=x2‎ 是 否是 是 否是 输出 结束 第10题图 ‎9.在长方体中，若，，则对角线的长为 A．B.C．D．‎ ‎10.给出一个如右图所示的程序框图，若要使输入的值与输出的值相等，则这样的的个数是 ‎ A．B．C．D．‎ ‎11.某程序框图如右图所示，若输出的，则判断框内应填 A． B．C． D．‎ ‎12.已知集合，，若 ‎，则实数的取值范围是 A．B． C． D．‎ 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13.则实数的的最大公约数是________．‎ ‎14.已知，当取最小值时的值为________．‎ ‎15.已知如下算法语句 输入t;‎ If t<5 Then y=t2+1; ‎ ‎ Else if t<8 Then y=2t-1;‎ ‎ Else y=;‎ ‎ End If ‎ End if 输出y 若输入t=8,则下列程序执行后输出的结果是.‎ ‎16.已知是直线上的动点，是圆的两条切线，是切点，是圆心，则四边形面积的最小值为．‎ 三、解答题：共70分。解答应写出文字说明、解答过程或演算步骤。‎ ‎17．（本小题满分10分）‎ 已知圆以原点为圆心，且与圆外切．‎ ‎（Ⅰ）求圆的方程； （Ⅱ）求直线与圆相交所截得的弦长．‎ ‎18.（本小题满分12分）‎ 已知数列的前项和，．‎ ‎（Ⅰ）求数列的通项公式；（Ⅱ）设，求数列的前项和．‎ ‎19．（本小题满分12分）‎ 某篮球学校的甲、乙两名运动员练习罚球，每人练习组，每组罚球个，命中个数的茎叶图如图．根据茎叶图求：‎ ‎（Ⅰ）甲、乙两名运动员命中个数的极差分别是多少？‎ ‎（Ⅱ）甲运动员命中个数在间的频率是多少？‎ ‎（Ⅲ）甲、乙两名运动员哪个罚球命中率较高？并简要说明．‎ ‎20．（本小题满分12分）‎ 在中,角所对的边分别为，满足,且. (Ⅰ)求的面积；(Ⅱ)若，求的值.‎ ‎21．（本小题满分12分）‎ 某校从参加高一年级期中考试的学生中随机抽出名学生，将其物理成绩(均为整数)分成六段后得到如图所示的频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；‎ ‎（Ⅱ）估计本次考试物理成绩的众数与中位数(中位数保留小数点后一位)；‎ ‎（Ⅲ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试数学成绩的平均分．‎ ‎22．（本小题满分12分）‎ 已知圆与直线相交于、两点，为原点，且，求实数的值．‎ 玉溪市民族中学高二第一次月考 数学试卷（文理同卷）‎ 参考答案 一、选择题：1-12：‎ 二、填空题：13、；14、；15、；16、‎ 三、解答题 ‎ ‎17．解：（Ⅰ）设圆方程为．圆，‎ ‎，所以圆方程为．‎ ‎（Ⅱ）到直线的距离为，‎ 故弦长．‎ ‎18.解：（Ⅰ）当时，；‎ ‎（Ⅱ）当时，，‎ 当时，也适合上式.因此，数列的通项公式为，‎ ‎（Ⅱ）由（Ⅰ）知，故，‎ ‎ 可知 ‎19.解：（Ⅰ）从茎叶图可以看出甲运动员的最大值是，最小值是，‎ 甲运动员的极差为；‎ 乙运动员的最大值是，最小值是，‎ 乙运动员的极差为.‎ ‎（Ⅱ）甲运动员命中个数在间的频数是，‎ 样本容量是，‎ ‎∴频率为.‎ ‎（Ⅲ）甲运动员的命中个数集中在茎叶图的下方，而乙运动员的命中个数集中在茎叶图的上方．‎ 从数据的分布情况来看，甲运动员的罚球命中率较高．‎ ‎20．解:(Ⅰ)因为,且 所以,∴, ∴, 又bc=5, 所以; (Ⅱ)因为, 所以, ∵bc=5,b2+c2=26, ∵根据余弦定理得:a2=b2+c2﹣2bccosA=, ∴.‎ ‎21.解：（Ⅰ）设分数在内的频率为，‎ 根据频率分布直方图，则有：‎ ‎，‎ ‎∴分数在内的频率为.‎ 频率分布直方图如图所示．‎ ‎（Ⅱ）∵分数在内的小矩形最高，众数是最高小矩形中点的横坐标，‎ ‎∴众数为.‎ ‎∵分数在内的频率为：，‎ ‎∴中位数在内，‎ ‎∵中位数要平分直方图的面积，‎ ‎∴中位数为：.‎ ‎（Ⅲ）利用组中值估算抽样学生的平均分为：‎ ‎，‎ 估计这次考试的平均分是.‎ ‎22．解:设点、的坐标为、．一方面，由，得 ‎，即，也即：．①‎ 另一方面，、是方程组的实数解，即、是方程②‎ 的两个根．‎ ‎∴，．③‎ 又、在直线上，‎ ‎∴．‎ 将③代入，得．④‎ 将③、④代入①，解得，代入方程②，检验成立，并且原方程为圆的方程.‎ ‎∴．‎