数学理卷·2018届河南省新乡市延津县高级中学高二（卫星班）下学期期末考试（2017-07）

数学理卷·2018届河南省新乡市延津县高级中学高二（卫星班）下学期期末考试（2017-07）

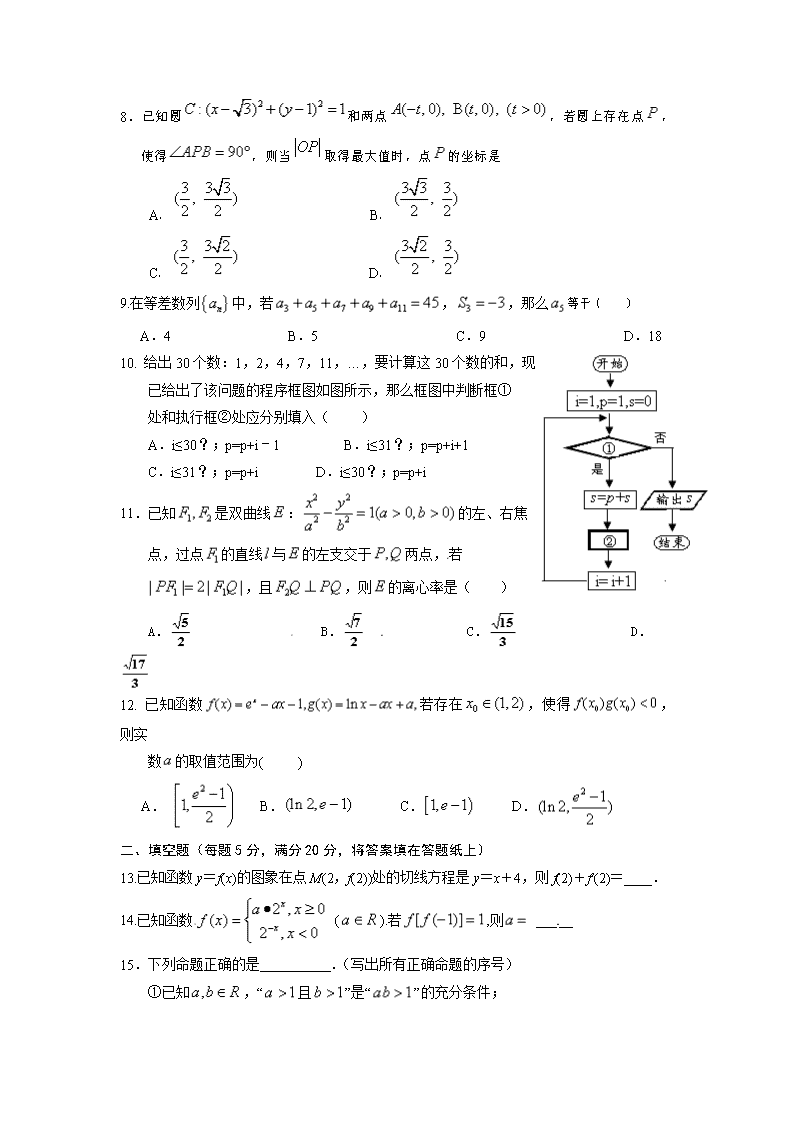
高二理科卫星班期末考试 数学(理科)试题 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 复数满足：，则（ ）【来源：全,品…中&高*考+网】‎ A． B． C． D． ‎ ‎2．已知是虚数单位，复数的虚部为 ‎ A. B. C. D. ‎ ‎3. 若，则（ ）‎ A． B． C． D． ‎ ‎4. 若，则直线被圆所截得的弦长为（ ）‎ A． B． C. D． ‎5. 将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的左视图为（ ）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ A B C D ‎6.为得到函数的图象，只需将函数的图象（ ）‎ A．向左平移个长度单位 B．向左平移个长度单位 C．向左平移个长度单位 D．向右平移个长度单位 ‎ ‎7.《九章算术》中“开立圆术”曰：“置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径”．“开立圆术”相当于给出了已知球的体积V，求其直径d，公式为．如果球的半径为，根据“开立圆术”的方法求球的体积为（ ）‎ A． B． C． D．‎ ‎8．已知圆和两点，若圆上存在点，使得，则当取得最大值时，点的坐标是 A． B． ‎ C． D．‎ ‎9.在等差数列中，若，，那么等于（ ）‎ A．4 B．‎5 ‎C．9 D．18‎ 10. ‎ 给出30个数：1，2，4，7，11，…，要计算这30个数的和，现 已给出了该问题的程序框图如图所示，那么框图中判断框①‎ 处和执行框②处应分别填入（　 　）‎ A．i≤30？；p=p+i﹣1 B．i≤31？；p=p+i+1‎ C．i≤31？；p=p+i D．i≤30？；p=p+i ‎11．已知是双曲线：的左、右焦 点，过点的直线与的左支交于两点，若 ‎，且，则的离心率是（ ）‎ A．         B．       C．        D．‎ ‎12. 已知函数若存在，使得，则实 ‎ 数的取值范围为( )‎ A． B． C． D． ‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.已知函数y＝f(x)的图象在点M(2，f(2))处的切线方程是y＝x＋4，则f(2)＋f′(2)＝____．‎ ‎14.已知函数 ().若,则 _____‎ ‎15．下列命题正确的是 ．（写出所有正确命题的序号）‎ ‎①已知，“且”是“”的充分条件；‎ ‎②已知平面向量，“且”是“”的必要不充分条件；‎ ‎③已知，“”是“”的充分不必要条件；‎ ‎④命题：“，使且”的否定为：“，‎ 都有且” ‎ ‎16. 已知函数是定义在的可导函数，为其导函数，当且时，，若曲线在处的切线的斜率为，则 ‎_________ ‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17.(本小题满分12分)‎ 设向量，记函数 ‎（1）求函数的单调递增区间；‎ ‎（2）在锐角中，角A,B，C的对边分别为，若，求面积的最大值．‎ ‎18.（本小题满分12分）‎ 已知数列{an}满足a1＝1，a2＝4，且对任意m，n，p，q∈N*，若m＋n＝p＋q，则有am＋an＝ap＋aq.‎ ‎(Ⅰ)求数列{an}的通项公式；‎ ‎(Ⅱ)设数列的前n项和为Sn，求证：≤Sn<.‎ ‎19. （本小题满分12分）‎ 在某城市气象部门的数据中，随机抽取100天的空气质量指数的监测数据如表：‎ 空气质量指数t ‎（0，50]‎ ‎（50，100]‎ ‎（100，150]‎ ‎（150，200）【来源：全,品…中&高*考+网】‎ ‎（200，300]‎ ‎（300，+∞）‎ 质量等级 优 良 轻微污染 轻度污染 中度污染 严重污染 天数K ‎5‎ ‎23‎ ‎22‎ ‎25‎ ‎15‎ ‎10‎ ‎（1）若该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t（t 取整数）存在如下关系y=且当t＞300时，y＞500，估计在某一医院收治此类病症人数超过200人的概率； ‎ ‎（2）若在（1）中，当t＞300时，y与t的关系拟合与曲线，现已取出了10对样本数据（ti，yi）（i=1，2，3，…，10）且知，，，，试用可线性化的回归方法，求拟合曲线的表达式．‎ ‎（附：线性回归方程中，，．）‎ ‎20．如图，四棱锥中，底面是 边长为4的正方形，平面平面，‎ ‎．‎ ‎（1）求证：平面平面；‎ ‎（2）为线段上一点，若二面角 的平面角与二面角的平面角大小相等，‎ 求的长．‎ ‎21. 已知在平面直角坐标系中，是坐标原点，动圆经过点，且与直线相切.‎ ‎（1）求动圆圆心的轨迹方程；【来源：全,品…中&高*考+网】‎ ‎（2）过的直线交曲线于两点，过作曲线的切线，直线交于点，求的面积的最小值.‎ 请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分 ‎22．（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系中，曲线C1的参数方程为（α为参数），以原点O 为极点，x轴的正半轴为级轴，建立极坐标系，曲线C2的极坐标方程；‎ ‎（I）求曲线C1的普通方程和曲线C2的直角坐标方程；‎ ‎（Ⅱ）设P为曲线C1上的动点，求点P到曲线C2上的距离的最小值的值并求此时点P的坐标；‎ ‎23．（本小题满分10分）选修4-5：不等式选讲 已知函数，‎ ‎（1）解不等式 ‎ （2）若对于，有，求证：．‎ 参考答案 ‎1—12：CAA B D A D B B D D A ‎13．7 14． 15．③ 16．‎ ‎17.‎ ‎ ‎ ‎（2）【来源：全,品…中&高*考+网】‎ 在中，利用余弦定理，即（当且仅时等号成立），即，又 ‎.（当且仅当时等号成立）‎ 面积的最大值为 ‎18．【解析】(Ⅰ)令m＝1，p＝n－1，q＝2，得an＋a1＝an－1＋a2.‎ 即an－an－1＝3(n≥2)．‎ 所以数列{an}是以3为公差的等差数列．‎ ‎∴an＝1＋(n－1)×3＝3n－2.(6分)‎ ‎(Ⅱ)因为＝＝.‎ 所以Sn＝＝<.‎ 另一方面，由于＝>0，‎ 则Sn≥S1＝＝＝.‎ 综上可知：≤Sn<.(12分)‎ ‎19．解：（1）令y＞200得2t-100＞200，解得t＞150， ∴当t＞150时，病人数超过200人． 由频数分布表可知100天内空气指数t＞150的天数为25+15+10=50． ∴病人数超过200人的概率P=． （2）令x=lnt，则y与x线性相关，==7，=600， ∴b===50，a=600-50×7=250． ∴拟合曲线方程为y=50x+250=50lnt+250． 20．(Ⅰ)∵平面平面，，∴平面 ∵底面，∴平面底面 (Ⅱ)取中点，连接 ‎，又因为平面底面，所以平面 以为原点，方向分别为轴正方向建立空间直角坐标系 平面的法向量， 平面的法向量， ， 则，∴ 设，所以 由上同理可求出平面的法向量 由平面、与平面所成的锐二面角的大小相等可得 ‎ ‎，∴ ∴‎ ‎21． ‎ ‎（2）设，直线 将代入中得 所以，，‎ 得切线： ‎ ‎22．解：（Ⅰ）由曲线C1：（α为参数），曲线C1的普通方程为：．‎ 由曲线C2：ρsin（π+）=4，展开可得：（sinθ+cosθ）=4，化为：x+y=8．‎ 即：曲线B的直角坐标方程为：x+y=8．…（5分）‎ ‎（Ⅱ）椭圆上的点到直线O的距离为 ‎∴当sin（α+φ）=1时，P的最小值为．…（10分）【来源：全,品…中&高*考+网】‎ ‎23．解：（1）不等式f（x）＜x+1，等价于|2x﹣1|＜x+1，即﹣x﹣1＜2x﹣1＜x+1，‎ 求得0＜x＜2，故不等式f（x）＜x+1的解集为（0，2）．‎ ‎（2）∵，‎ ‎∴f（x）=|2x﹣1|=|2（x﹣y﹣1）+（2y+1）|≤|2（x﹣y﹣1）|+|（2y+1）|≤2•+＜1．‎