- 2021-06-11 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020届艺术生高考数学二轮复习课时训练:第六章 不等式、推理与证明 第3节
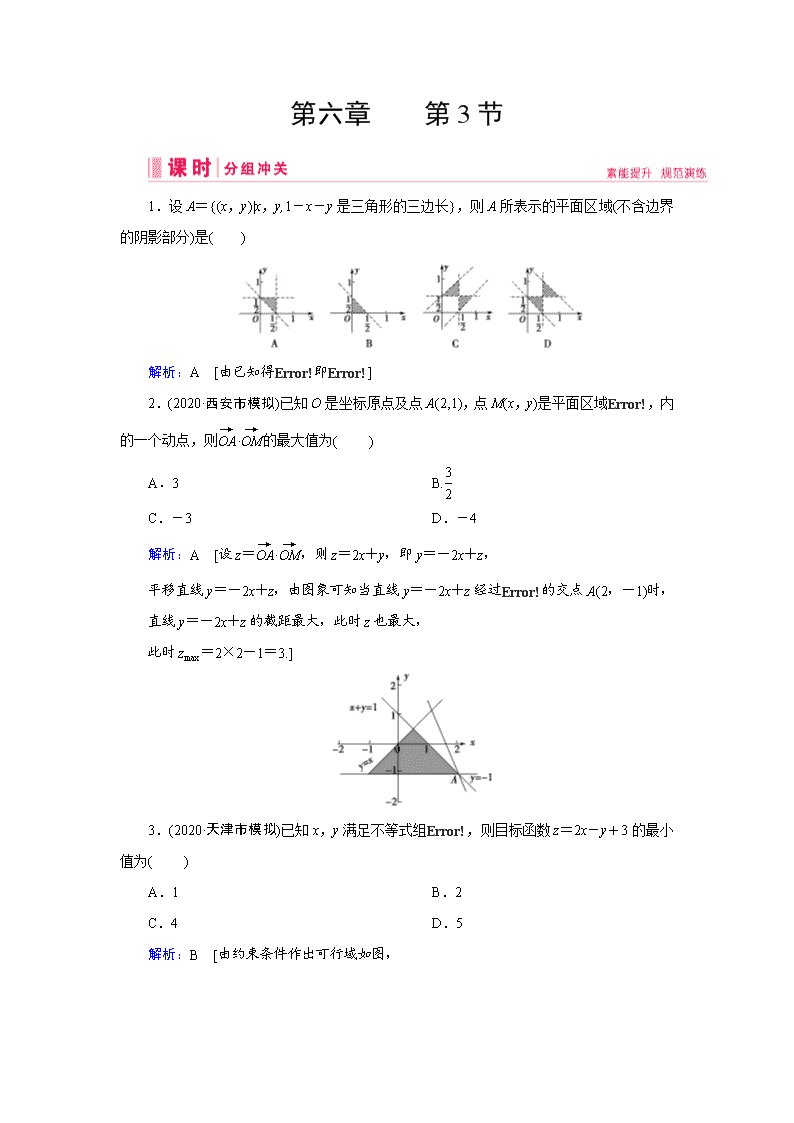
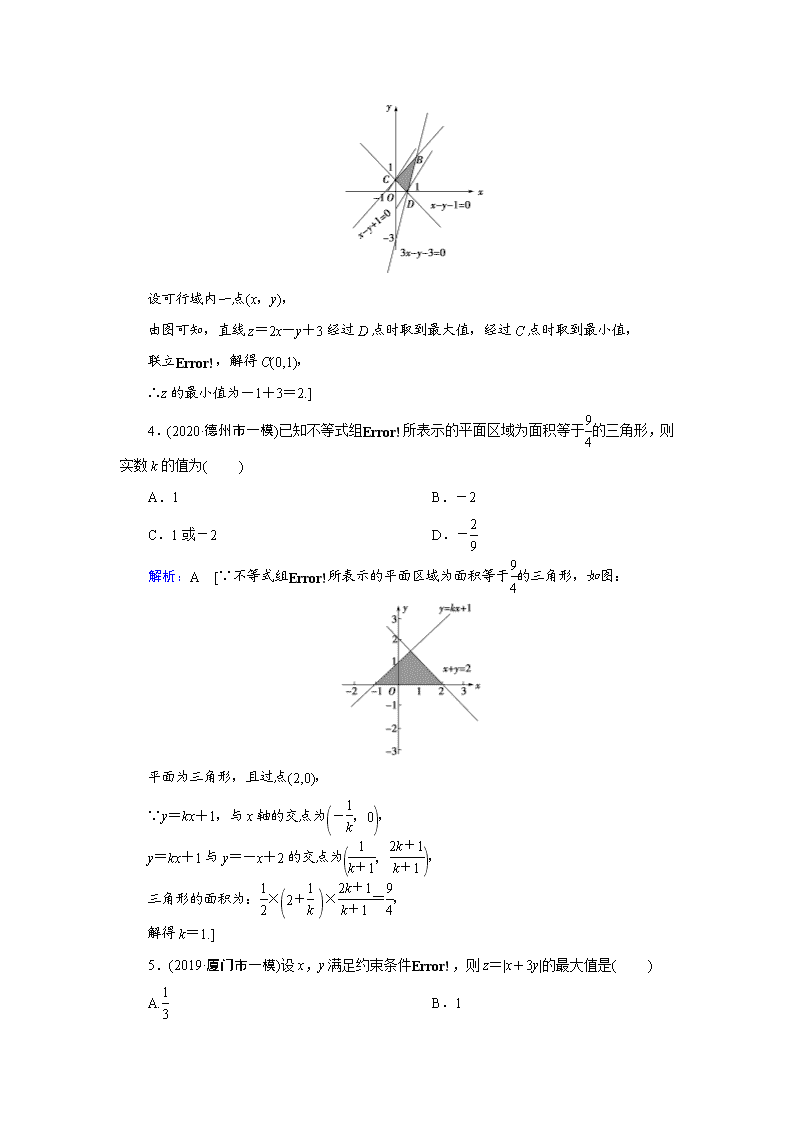
第六章 第3节 1.设A={(x,y)|x,y,1-x-y是三角形的三边长},则A所表示的平面区域(不含边界的阴影部分)是( ) 解析:A [由已知得即] 2.(2020·西安市模拟)已知O是坐标原点及点A(2,1),点M(x,y)是平面区域,内的一个动点,则·的最大值为( ) A.3 B. C.-3 D.-4 解析:A [设z=·,则z=2x+y,即y=-2x+z, 平移直线y=-2x+z,由图象可知当直线y=-2x+z经过的交点A(2,-1)时, 直线y=-2x+z的截距最大,此时z也最大, 此时zmax=2×2-1=3.] 3.(2020·天津市模拟)已知x,y满足不等式组,则目标函数z=2x-y+3的最小值为( ) A.1 B.2 C.4 D.5 解析:B [由约束条件作出可行域如图, 设可行域内一点(x,y), 由图可知,直线z=2x-y+3经过D点时取到最大值,经过C点时取到最小值, 联立,解得C(0,1), ∴z的最小值为-1+3=2.] 4.(2020·德州市一模)已知不等式组所表示的平面区域为面积等于的三角形,则实数k的值为( ) A.1 B.-2 C.1或-2 D.- 解析:A [∵不等式组所表示的平面区域为面积等于的三角形,如图: 平面为三角形,且过点(2,0), ∵y=kx+1,与x轴的交点为, y=kx+1与y=-x+2的交点为, 三角形的面积为:××=, 解得k=1.] 5.(2019·厦门市一模)设x,y满足约束条件,则z=|x+3y|的最大值是( ) A. B.1 C. D.2 解析:D [画出x,y满足约束条件表示的平面区域, 由解得B, 由解得A(-1,1), 由解得C. 设目标函数为z′=x+3y,作出目标函数对应的直线, 直线过C时,直线的纵截距最小,z′最小,最小值为-;当直线过A(-1,1)时,直线的纵截距最大,z′最大,最大值为2;∴目标函数z=|x+3y|的取值范围是[0,2],最大值为2.] 6.(2019·泉州市模拟)若x,y满足约束条件,则z=x2+y2的最小值为 _____ . 解析:不等式组表示的平面区域如图所示, 则z=x2+y2的几何意义为区域内的点到原点的距离的平方, 由图象知,OA的距离最小, 由,解得A(0,1), 所以|OA|2=1, 所以z=x2+y2的最小值为1. 答案:1 7.若不等式组,表示的平面区域的面积为3,则实数a的值是 ________ . 解析:作出可行域,如图中阴影部分所示,区域面积 S=××2=3,解得a=2. 答案:2 8.(2019·聊城市一模)设x,y满足约束条件,则z=2xy的最大值为 ________ . 解析:画出约束条件表示的平面区域,如图所示; 又z=2xy=2x·2-4y=2x-4y, 设t=x-4y, 则目标函数t=x-4y过点B时,取得最大值, 由,得B(-2,-1); ∴z的最大值为2-2-4×(-1)=4. 答案:4 9.(2019·杭州市高三模拟)若实数x,y满足. 求:(1)x的取值范围; (2)|x|+|y|的取值范围. 解: (1)由约束条件作出可行域如图, 由图可知,0≤x≤1. (2)当x≥0,y≥0时, z=|x|+|y|=x+y过时有最大值为, 过O(0,0)时有最小值0; 当x≥0,y≤0时,z=|x|+|y|=x-y过(1,-1)时有最大值为2, 过O(0,0)时有最小值0.所以|x|+|y|的取值范围是[0,2]. 10.若x,y满足约束条件 (1)求目标函数z=x-y+的最值; (2)若目标函数z=ax+2y仅在点(1,0)处取得最小值,求a的取值范围. 解:(1)作出可行域如图,可求得A(3,4),B(0,1),C(1,0). 平移初始直线x-y+=0,过A(3,4)时z取最小值-2,过C(1,0)时z取最大值1. 所以z的最大值为1,最小值为-2. (2)直线ax+2y=z仅在点(1,0)处取得最小值,由图象可知-1<-<2, 解得-4查看更多
相关文章
- 当前文档收益归属上传用户