甘肃省庆阳市宁县第二中学2019-2020高一下学期4月线上测试数学试题

甘肃省庆阳市宁县第二中学2019-2020高一下学期4月线上测试数学试题

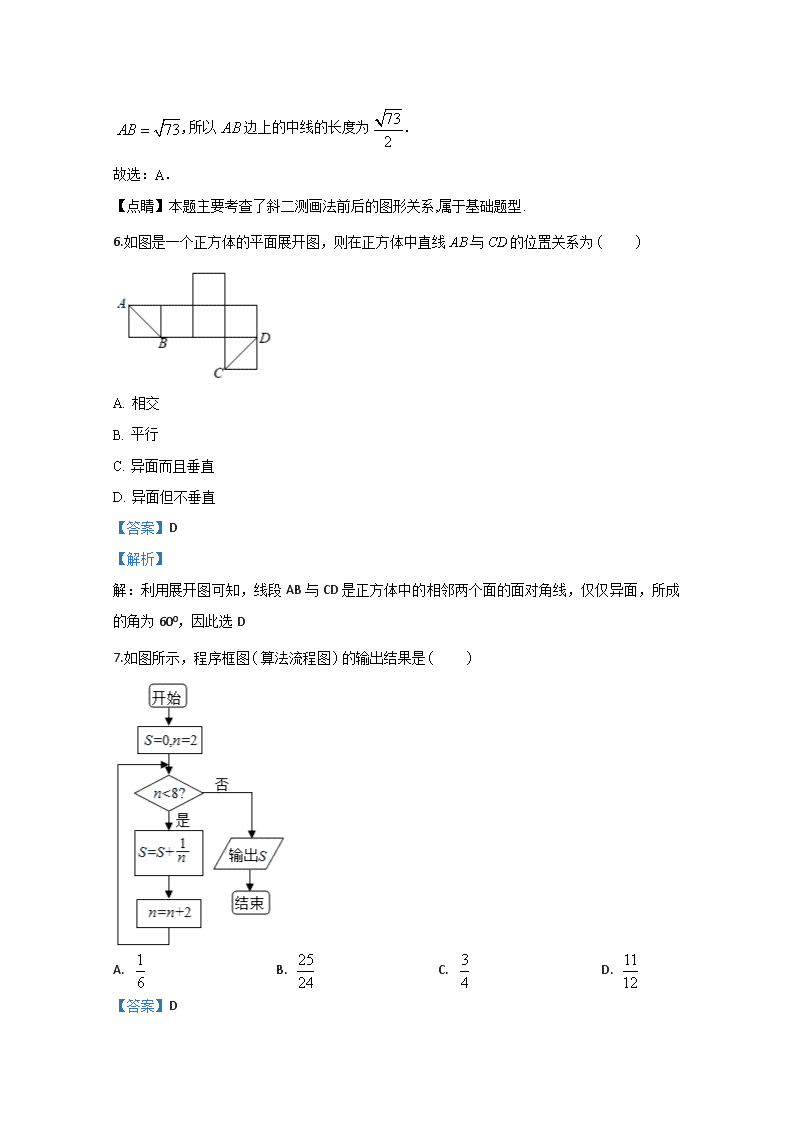
数学试卷 第Ⅰ卷 一、 选择题（每小题5分，共50分）‎ ‎1.若奇函数在上为增函数，且有最小值0，则它在上 （ ）‎ A. 是减函数，有最小值0‎ B. 是增函数，有最小值0‎ C. 是减函数，有最大值0‎ D. 是增函数，有最大值0‎ ‎【答案】D ‎【解析】‎ ‎【详解】因为为奇函数，且在上为增函数，且有最小值0，‎ 所以在上增函数，且有最大值0，选D.‎ ‎2.函数(，且)的图象恒过定点（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 令中即可 详解】解：当时，，所以，‎ 所以函数图象恒过点 故选：D．‎ ‎【点睛】考查指数型函数恒过定点，基础题.‎ ‎3.函数y＝ ＋log2(x＋3)的定义域是(　　)‎ A. R B. (－3，＋∞) C. (－∞，－3) D. (－3,0)∪(0，＋∞)‎ ‎【答案】D ‎【解析】‎ 试题分析：由题意,得，解得.故选D.‎ 考点：函数的定义域.‎ ‎4.已知集合，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ ‎，直接求交集即可 ‎【详解】解：由题意得，‎ 故选：D．‎ ‎5.水平放置的的斜二测直观图如图所示,已知,,轴,则中边上的中线的长度为( )‎ A. B. C. 5 D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据斜二测画法的规则还原图形的边角关系再求解即可.‎ ‎【详解】由斜二测画法规则知,即直角三角形,其中,,所以 ‎,所以边上的中线的长度为.‎ 故选：A.‎ ‎【点睛】本题主要考查了斜二测画法前后的图形关系,属于基础题型.‎ ‎6.如图是一个正方体的平面展开图，则在正方体中直线AB与CD的位置关系为　　‎ A. 相交 B. 平行 C. 异面而且垂直 D. 异面但不垂直 ‎【答案】D ‎【解析】‎ 解：利用展开图可知，线段AB与CD是正方体中的相邻两个面的面对角线，仅仅异面，所成的角为600，因此选D ‎7.如图所示，程序框图算法流程图的输出结果是　　‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 模拟程序图框的运行过程，得出当时，不再运行循环体，直接输出S值．‎ ‎【详解】模拟程序图框运行过程，得 S=0,n=2,n<8满足条件，进入循环：‎ S=满足条件，进入循环：‎ 进入循环：‎ 不满足判断框的条件，进而输出s值，‎ 该程序运行后输出的是计算：．‎ 故选D．‎ ‎【点睛】本题考查了程序框图的应用问题，是基础题目．根据程序框图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：①分析流程图（或伪代码），从流程图（或伪代码）中即要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．‎ ‎8.三个数0.32，20.3，的大小关系为（ ）.‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用指数函数与对数函数的单调性即可得出．‎ ‎【详解】∵0＜0.32＜1，20.3＞1，log0.32＜0，‎ ‎∴20.3＞0.32＞log0.32．‎ 故选A．‎ ‎【点睛】本题考查了指数函数与对数函数的单调性，属于基础题．‎ ‎9.一个球的内接正方体的表面积为54，则球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 分析】‎ 球的内接正方体的对角线就是球的直径，正方体的棱长为a，球的半径为r，则，求出正方体棱长，再求球半径即可 ‎【详解】解：设正方体的棱长为a，球的半径为r，‎ 则，所以．‎ 又因为 所以 所以 故选：A ‎【点睛】考查球内接正方体棱长和球半径的关系以及球表面积的求法，基础题.‎ ‎10.过点且垂直于直线的直线方程为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由题，可先得到所求直线的斜率，然后利用点斜式，即可得到本题答案.‎ ‎【详解】因为所求直线垂直于直线，又直线的斜率为，‎ 所以所求直线的斜率，‎ 所以直线方程为，即.‎ 故选：A ‎【点睛】本题主要考查直线方程的求法，属基础题.‎ ‎11.已知函数y＝|x－3|，如图所示程序框图表示的是给定x值，求其相应函数值的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎(1)因为y＝|x－3|，所以需对x－3的正负进行判断．故判断框内应为x<3？因为“是”时，y＝3－x. 所以“否”时，即x≥3时，y＝x－3．‎ ‎12.方程的解__________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ ‎,用真数相等即可，注意真数大于零.‎ ‎【详解】解：∵，‎ ‎∴，‎ ‎∴‎ 经检验满足 故答案为：.‎ ‎【点睛】考查简单对数方程的解法，基础题.‎ 三、解答题（13，14题每小题13分，15题14分，共40分）‎ ‎13.设 ‎（1）讨论的奇偶性;‎ ‎（2）判断函数在上的单调性并用定义证明.‎ ‎【答案】(1)奇函数(2)在上是增函数，证明见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎(1)分别确定函数定义域和与的关系即可确定函数的奇偶性；‎ ‎(2),且,通过讨论的符号决定与的大小，据此即可得到函数的单调性.‎ ‎【详解】(1)的定义域为,,是奇函数.‎ ‎(2),且,‎ ‎∵,，‎ ‎ ， .‎ ‎ 在上是增函数.‎ ‎【点睛】本题主要考查函数的奇偶性，函数的单调性的证明等知识，意在考查学生的转化能力和计算求解能力.‎ ‎14.设集合或，分别求出满足下列条件的实数的取值范围：‎ ‎（1） ‎ ‎（2） ‎ ‎【答案】（1）；（2）或．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先解出，时，看集合与的端点大小即可（2）当时，有，所以或.‎ ‎【详解】解：（1）∵‎ ‎∴‎ 当时，有，解得 故答案为：．‎ ‎（2）当时，有，所以或，‎ 解得或 故答案为：或．‎ ‎【点睛】考查已知两个集合的关系求参数的取值范围，中档题.‎ ‎15.如图在三棱锥中， 分别为棱的中点，已知.‎ 求证：（1）直线平面；‎ ‎（2）平面 平面.‎ ‎【答案】(1)证明见解析；（2）证明见解析．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）本题证明线面平行，根据其判定定理，需要在平面内找到一条与平行的直线，由于题中中点较多，容易看出，然后要交待在平面外，在平面 内，即可证得结论；（2）要证两平面垂直，一般要证明一个平面内有一条直线与另一个平面垂直，由（1）可得，因此考虑能否证明与平面内的另一条与相交的直线垂直，由已知三条线段的长度，可用勾股定理证明，因此要找的两条相交直线就是，由此可得线面垂直.‎ ‎【详解】（1）由于分别是的中点，则有，又平面，平面，所以平面．‎ ‎（2）由（1），又，所以，又是中点，所以，，又，所以，所以，是平面内两条相交直线，所以平面，又平面，所以平面平面．‎ ‎【考点】线面平行与面面垂直．‎ ‎ ‎ ‎ ‎