- 2021-06-11 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年甘肃省静宁县第一中学高二下学期期末考试数学(文)试题 Word版
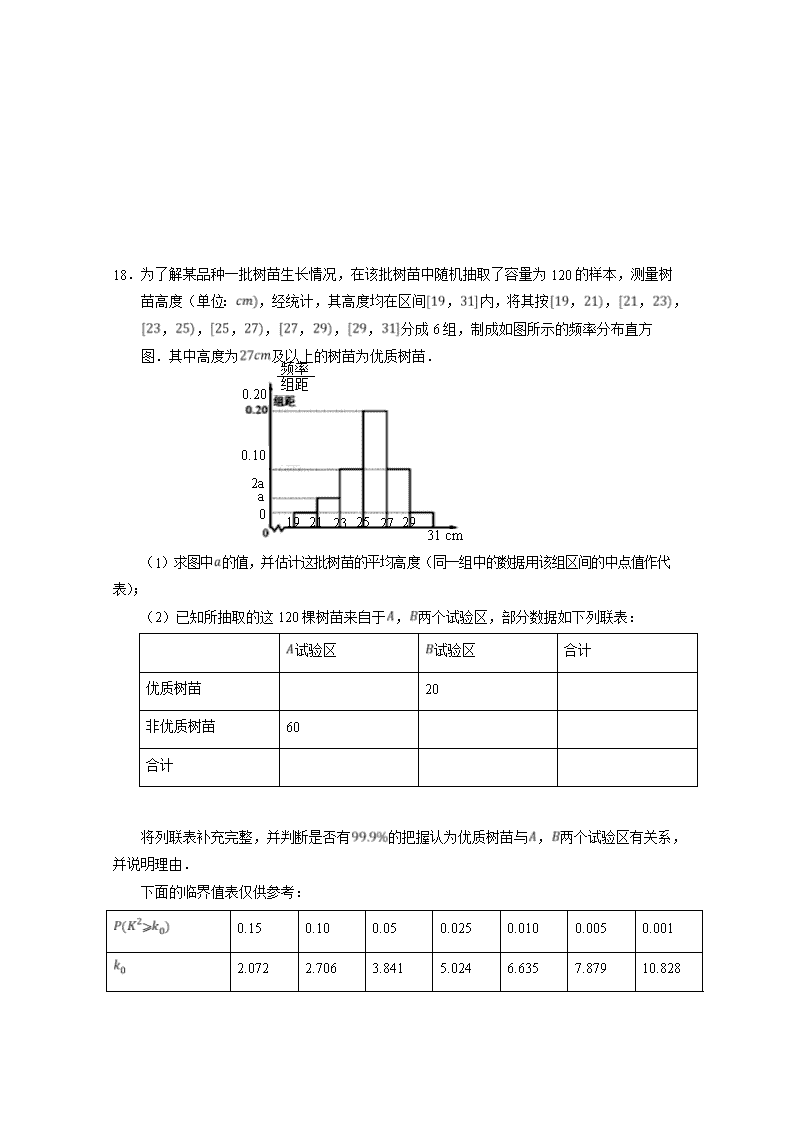
静宁一中2018-2019学年度第二学期高二级期末试题(卷) 数学(文科) 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.复数( ) A. B. C. D. 2.设集合,1,2,3,,,2,,,3,,则( ) A., B., C. ,1, D.,2, 3.已知平面向量,的夹角为,,,则( ) A.3 B.2 C.0 D. 4.已知函数,则( ) A.的最小正周期是,最大值是1 B.的最小正周期是,最大值是 C.的最小正周期是,最大值是 D.的最小正周期是,最大值是1 5.若,则下列不等式恒成立的是( ) A. B. C. D. 6.某程序框图如图所示,该程序运行后输出的值是( ) A.55 B.45 C.66 D.36 7.抛物线的焦点到双曲线的渐近线的距离是( ) A. B. C. D. 8.函数的图象大致是( ) 9.在中,,,,则的面积为( ) A.15 B. C.40 D. 10..函数在上的最小值为( ) A. -2 B.0 C. D. 11.法国机械学家莱洛. 发现了最简单的等宽曲线莱洛三角形,它是分别以正三角形的顶点为圆心,以正三角形边长为半径作三段圆弧组成的一条封闭曲线,在封闭曲线内随机取一点,则此点取自正三角形之内(如图阴影部分)的概率是( ) A. B. C. D. 12.定义域为R的可导函数的导函数为,满足,且,则不等式的解集为( ) A. B. C. D. 二、填空题:本题共4小题,每小题5分,共20分 13.若是第四象限角,,则_____.. 14.在正方体中,,分别为,中点,则异面直线与所成角的余弦值为_____. 15.若实数,满足约束条件,则的最大值是_____. 16.已知函数,且,则_____. 三、解答题:共70分解答应写出文字说明、证明过程或演算步骤 17.已知等差数列满足,. (1)求的通项公式; (2)设是等比数列的前项和,若,,求. 频率 组距 0.20 0.10 2a a 0 199 219 239 259 279 299 18.为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:,经统计,其高度均在区间,内,将其按,,,,,,,,,,,分成6组,制成如图所示的频率分布直方图.其中高度为及以上的树苗为优质树苗. 31 cm (1)求图中的值,并估计这批树苗的平均高度(同一组中的数据用该组区间的中点值作代表); 试验区 试验区 合计 优质树苗 20 非优质树苗 60 合计 (2)已知所抽取的这120棵树苗来自于,两个试验区,部分数据如下列联表: 将列联表补充完整,并判断是否有的把握认为优质树苗与,两个试验区有关系,并说明理由. 下面的临界值表仅供参考: 0.15 0.10 0.05 0.025 0.010 0.005 0.001 2.072 2.706 3.841 5.024 6.635 7.879 10.828 (参考公式:,其中. 19. (本小题满分12分)在直三棱柱(侧棱垂直底面)中, 平面,其垂足落在直线上. (1)求证:; (2)若,,为的中点,求三棱锥的体积. 20.已知函数. (1)求曲线在点处的切线方程; (2)若在上恒成立,求实数的取值范围. 21.已知椭圆:的离心率为,且经过点. (1)求椭圆的方程; (2)与轴不垂直的直线经过,且与椭圆交于,两点,若坐标原点在以为直径的圆内,求直线斜率的取值范围. 选考题:共10分,请考生在第22、23题中选定一题作答 选修4-4:坐标系与参数方程 22.在直角坐标系中,直线的参数方程为(为参数).以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为. (1)求曲线的直角坐标方程; (2)若直线与曲线相交于不同的两点,,若是的中点,求直线的斜率. 选修4-5:不等式选讲 23.已知函数. (1)解不等式:; (2)已知.且对于,恒成立,求实数的取值范围. 2019年高二数学试卷(文科)答案 一、 选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答数 A C C B D A C A B D B C 二、填空题:本题共4小题,每小题5分,共20分 13. ; 14.; 15. 8; 16.16 三、解答题:共70分解答应写出文字说明、证明过程或演算步骤 17.【解】(I)设等差数列的公差为,∵.∴,, 解得,, ∴. (Ⅱ)设等比数列的公比为,,,联立解得,, ∴,或. 18.【解】(1)由频率分布直方图知,,解得, 计算, 估计这批树苗的平均高度为; (2)优质树苗有,根据题意填写列联表, 试验区 试验区 合计 优质树苗 10 20 30 非优质树苗 60 30 90 合计 70 50 120 计算观测值, 没有的把握认为优质树苗与,两个试验区有关系. 19.【解】(1)∵三棱柱为直三棱柱,∴平面, 又∵平面,∴,∵平面,且平面,∴, 又∵平面,平面,, ∴平面,又∵平面,∴; …………………… 5分 (2)在直三棱柱 中,, ∵平面,其垂足落在直线上,∴, 在中, ,,,, 在中,, …………………… 8分 由(1)知平面,平面,从而,, ∵为的中点,,…………………… 10分 ∴.…………………… 12分 20【解析】(1),, (1),又(1),即切线的斜率,切点为, 曲线在点处的切线方程; (2)令,,则, 令,则. 当时,,函数在上为增函数,故(1); 从而,当时,(1). 即函数在上为增函数,故(1). 因此,在上恒成立,必须满足. 实数的取值范围为,. 21.【解】(Ⅰ)由题意可得,解得,, ∴椭圆的方程为. (Ⅱ)设直线的方程为,代入椭圆方程整理可得得, ,解得或, 设,, 又,, ∴, ∵坐标原点在以为直径的圆内, ∴, ∴ , 解得或. 故直线斜率的取值范围为. 选考题:共10分,请考生在第22、23题中选定一题作答 选修4-4:坐标系与参数方程 22.【解】(Ⅰ)由,,,得 即所求曲线的直角坐标方程为: (Ⅱ)将直线的参数方程代入曲线的直角坐标方程,得 由是的中点知, 即[来源:Z,xx,k.Com] 所以直线的斜率为. 选修4-5:不等式选讲 23.【解析】(1), 当时,由,解得; 当时,不成立; 当时,由,解得. 所以不等式的解集为. (2)∵,∴ ∴对于,恒成立等价于:对,,即 ∵ ∴,∴ 查看更多