- 2021-06-11 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年四川省宜宾市高二下学期第一次月考数学试题(文)(Word版)
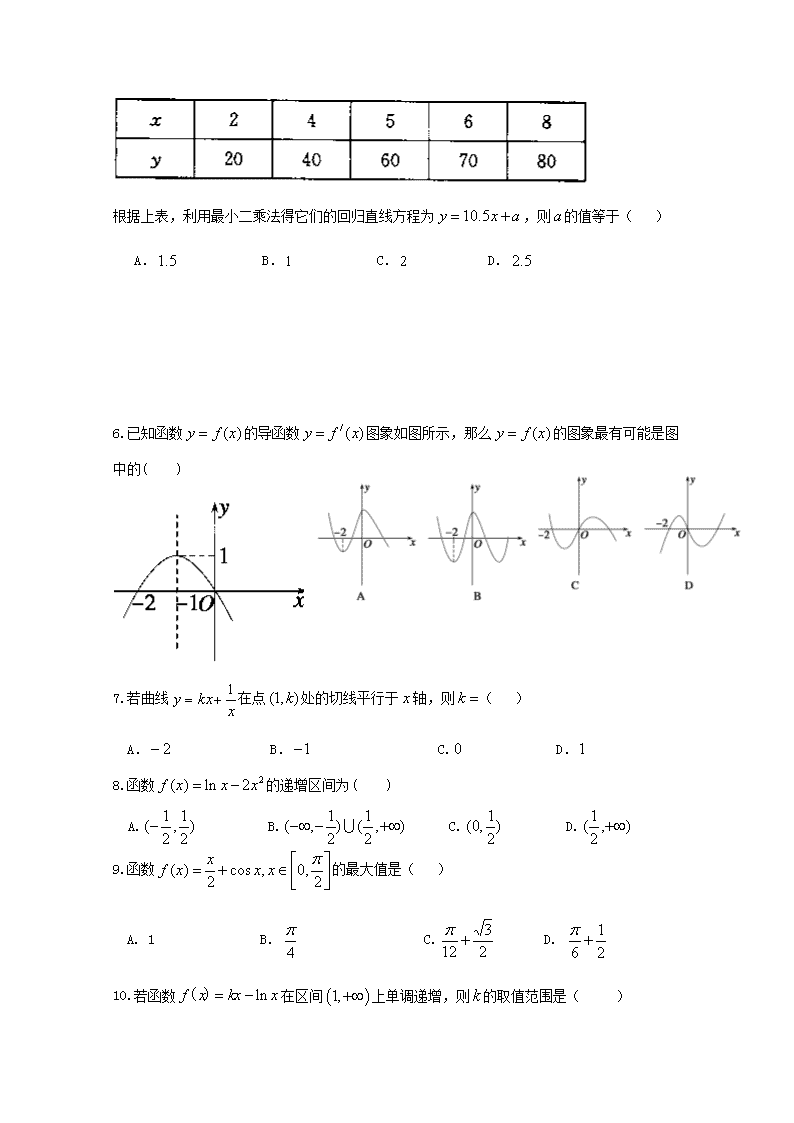
四川省宜宾市2017-2018学年高二数学下学期第一次月考试卷(文) 考试时间共 120 分钟,满分 150 分 试卷分为第Ⅰ卷(选择题)第Ⅱ卷(非选择题) 注意事项: 1.答题前,考生务必在答题卡上将自己的姓名、班级、准考证号用 0.5 毫米黑色签字笔填写清楚,考生考试条码由监考老师粘贴在答题卡上的“条码粘贴处”。 2.选择题使用 2B 铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡 皮擦擦干净后再填涂其它答案;非选择题用 0.5 毫米黑色签字笔在答题卡的对应区域 内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。 3.考试结束后由监考老师将答题卡收回。 第Ⅰ卷 (选择题,共 60 分) 一、选择题(本大题共 12 小题,每小题 5 分,共 60 分;在每小题给出的四个选项中, 只有一个是符合题目要求的) 1.已知满足,则分别等于( ) A. B. C. D. 2.命题“,”的否定是( ) A., B., C., D., 3.已知函数,则的值为( ) A. B. C. D. 4.用反证法证明“三角形中至少有一个内角不小于60°”,应先假设这个三角形中( ) A.有一个内角小于60° B.有一个内角大于60° C.每一个内角都小于60° D.每一个内角都大于60° 5.对具有线性相关关系的变量,,测得一组数据如下表: 根据上表,利用最小二乘法得它们的回归直线方程为,则的值等于( ) A. B. C. D. 6.已知函数的导函数图象如图所示,那么的图象最有可能是图中的( ) 7.若曲线在点处的切线平行于轴,则( ) A. B. C. D. 8.函数的递增区间为( ) A. B. C. D. 9.函数的最大值是( ) A. 1 B. C. D. 10.若函数在区间上单调递增,则的取值范围是( ) A. B. C. D. 11.若函数在内有极小值,则实数的取值范围是( ) A.(0,3) B. C.(0,+) D.(0,) 12.已知函数,若存在,使得,则实数的取值范围是( ) A. B. C. D. 第Ⅱ卷 (非选择题,共 90 分) 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分) 13.已知复数(为虚数单位),则= . 14.已知点的极坐标为,则点的直角坐标为 . 15.已知为偶函数,当,则曲线在点处的切线方程是________. 16.《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”:,,,,则按照以上规律,若具有“穿墙术”,则 . 三、解答题(本大题共 6 小题,第 17 题满分 10 分,18-22 每题满分 12 分,共 70 分; 解答应写出文字说明、证明过程或演算步骤) 17.(本题满分10分)已知复数,(,为虚数单位). (1)若是纯虚数,求实数的值; (2)若复数在复平面上对应的点在第四象限,求实数的取值范围. 18.(本题满分12分)已知圆和圆的极坐标方程分别为, (1) 把圆和圆的极坐标方程化为直角坐标方程; (2) 求经过两圆交点的直线的极坐标方程. 19.(本题满分12分)已知命题:关于的方程有实根;命题:对任意,不等式恒成立,若“”是假命题,“”也是假命题,求实数的取值范围; 20.(本题满分12分)北京时间4月14日,是湖人当家球星科比·布莱恩特的退役日,当天有大量网友关注此事。某网上论坛有重庆网友200人,四川网友300人。为了解不同地区对“科比退役”事件的关注程度,现采用分层抽样的方法,从中抽取100名网友,先分别统计他们在论坛的留言条数,再将留言条数分成5组:分别加以统计,得到如图所示的频率分布直方图。 规定留言不少于60条为“强烈关注”,否则为“一般关注”。 网友 强烈关注 一般关注 合计 重庆市 四川省 合计 完成上表,并判断是否有90%以上的把握认为关注程度与网友所在地区有关? 附:临界值表及参考公式:。 0.15 0.10 0.05 0.025 0.010 0.005 0.001 2.072 2.706 3.841 5.024 6.635 7.879 10.828 21.(本题满分12分) 已知,其中是自然常数, (1)若时,求的单调区间和极值; (2)是否存在实数,使得的最小值为,若存在求出的值;若不存在,请说明理由; 22.(本题满分12分)已知函数(为实数). (1)当时,求函数的图象在点处的切线方程; (2)设函数(其中为常数),若函数在区间上不存在极值,且存在满足,求的取值范围; 文科数学参考答案及评分建议 一、选择题:(每小题5分,共60分) 1.A; 2.B; 3.B; 4.C; 5.A; 6.A; 7.D; 8.C; 9.C; 10.D; 11.D; 12.C; 二、填空题(每小题5分,共20分) 13. ; 14.; 15 . ; 16 . ; 三、解答题(共70分) 17.解:(1)依据...............2分 根据题意是纯虚数,..............4分,;..............5分 (2)根据题意在复平面上对应的点在第四象限,可得 所以,实数的取值范围为..............10分 18.解:(1)由知,所以圆:;..............4分 由, 所以圆:...............8分 (2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为...............10分 化为极坐标方程为...............12分 19. 解::关于的方程有实根 则 或. 所以为真时............................3分 :对任意,不等式恒成立, 则由对任意 ,不等式 x-1≥a2-3a恒成立 ∴( x-1)min≥a2-3a 即a2-3a≤-2 解得1≤a≤2 , 即 为真命题时,a 的取值范围是1≤a≤2 . .........................8分 ∵“”是假命题,“”也是假命题,则是真命题,是假命题..............9分 ........................11分 ∴实数的取值范围为........................12分 20.解:根据分层抽样原理,重庆抽取100×=40人, 所以四川抽取60人; 重庆“强烈关注”有人,则“一般关注”有8人 四川“强烈关注”有人,则“一般关注”有21人 填写列联表如下; 网友 强烈关注 一般关注 合计 重庆市 a=32 b=8 40 四川省 c=39 d=21 60 合计 71 29 100 ..... ......6分 根据列联表,计算观测值 对照临界值表知,没有90%以上的把握认为关注程度与网友所在地区有关。............12分 21.解:(1), ……1分 ∴当时,,此时单调递减 当时,,此时单调递增 ……3分 ∴的极小值为 ,无极大值 ……5分 (Ⅲ)假设存在实数,使()有最小值3, ……6分 ① 当时,在上单调递减,,(舍去),所以,此时最小值的最小值不是3. ……7分 ②当时,在上单调递减,在上单调递增 ,,满足条件. ……9分 ③ 当时,在上单调递减,,(舍去),所以,此时最小值的最小值不是3.……11分 综上可知存在实数,使得当时有最小值3. ……12分 22.解:(1)当时,,, 则, 函数的图象在点的切线方程为:, 即 ……5分 (Ⅱ),由 由于函数在区间上不存在极值,所以或 ……6分 由于存在满足,所以 ……7分 对于函数,对称轴 ①当或,即或时,, 由,结合或可得:或 ②当,即时,, 由,结合可知:不存在; ③当,即时,; 由,结合可知: 综上可知: 或 ……12分 查看更多