- 2021-06-11 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013届人教A版文科数学课时试题及解析(44)直线、平面垂直的判定与性质B
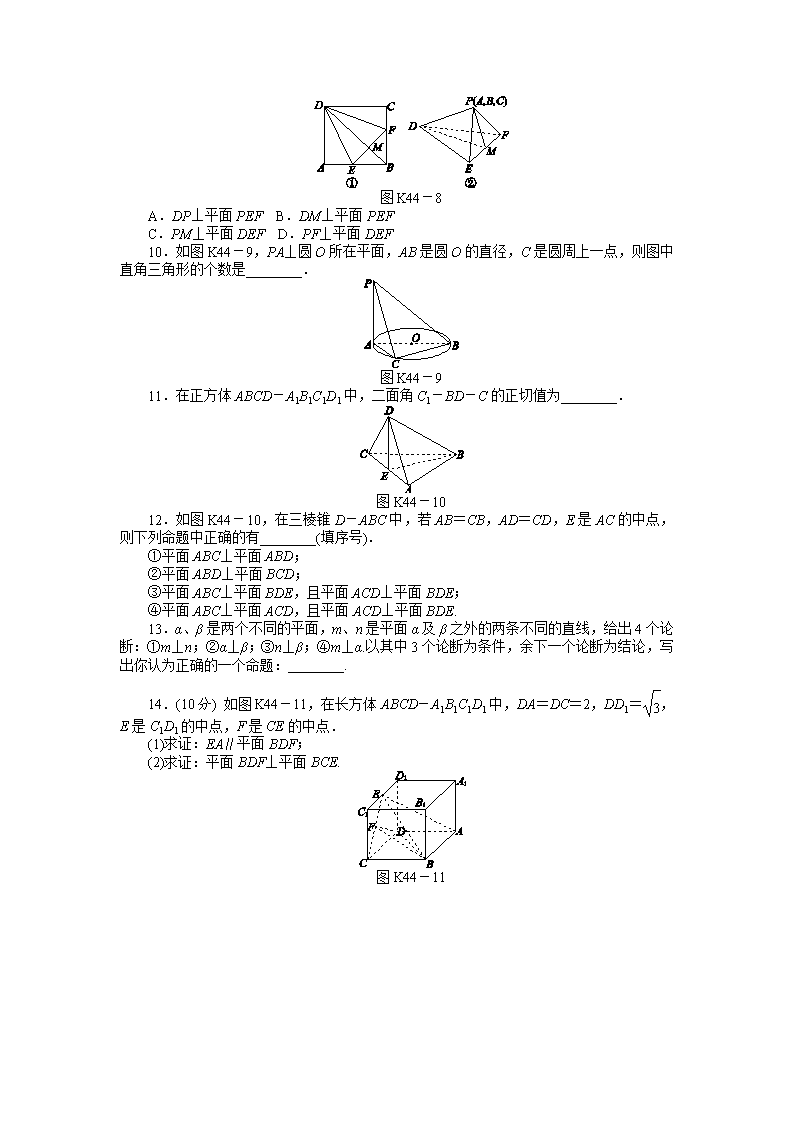
课时作业(四十四)B [第44讲 直线、平面垂直的判定与性质] [时间:45分钟 分值:100分] 1.已知m是平面α的一条斜线,点A∉α,l为过点A的一条动直线,那么下列情形可能出现的是( ) A.l∥m,l⊥α B.l⊥m,l⊥α C.l⊥m,l∥α D.l∥m,l∥α 2.已知直线l、m,平面α、β,且l⊥α,m⊂β,则α∥β是l⊥m的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 3. 在下列关于直线l,m与平面α,β的命题中,真命题是( ) A.若l⊂β且α⊥β,则l⊥α B.若l⊥β且α∥β,则l⊥α C.若l⊥β且α⊥β,则l∥α D.若α∩β=m且l∥m,则l∥α 4.如图K44-7所示,平面ABC⊥平面BDC,∠BAC=∠BDC=90°,且AB=AC=a,则AD=________. 图K44-7 5. 若a、b是空间两条不同的直线,α、β是空间的两个不同的平面,则a⊥α的一个充分条件是( ) A.a∥β,α⊥β B.a⊂β,α⊥β C.a⊥b,b∥α D.a⊥β,α∥β 6. 设a,b,c是空间不重合的三条直线,α,β是空间两个不同的平面,则下列命题中,逆命题不成立的是( ) A.当c⊥α时,若c⊥β,则α∥β B.当b⊂α时,若b⊥β,则α⊥β C.当b⊂α,且c是a在α内的射影时,若b⊥c,则a⊥b D.当b⊂α,且c⊄α时,若c∥α,则b∥c 7.正方形ABCD的边长是12,PA⊥平面ABCD,PA=12,那么P到对角线BD的距离是( ) A.12 B.12 C.6 D.6 8.已知P是△ABC所在平面外一点,PA,PB,PC两两垂直,且P在△ABC所在平面内的射影H在△ABC内,则H一定是△ABC的( ) A.内心 B.外心 C.垂心 D.重心 9.如图K44-8,在正方形ABCD中,E,F分别是AB,BC的中点,现在沿DE,DF及EF把△ADE,△CDF和△BEF折起,使A,B,C三点重合,重合后的点记作P,那么在四面体P-DEF中必有( ) 图K44-8 A.DP⊥平面PEF B.DM⊥平面PEF C.PM⊥平面DEF D.PF⊥平面DEF 10.如图K44-9,PA⊥圆O所在平面,AB是圆O的直径,C是圆周上一点,则图中直角三角形的个数是________. 图K44-9 11.在正方体ABCD-A1B1C1D1中,二面角C1-BD-C的正切值为________. 图K44-10 12.如图K44-10,在三棱锥D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列命题中正确的有________(填序号). ①平面ABC⊥平面ABD; ②平面ABD⊥平面BCD; ③平面ABC⊥平面BDE,且平面ACD⊥平面BDE; ④平面ABC⊥平面ACD,且平面ACD⊥平面BDE. 13.α、β是两个不同的平面,m、n是平面α及β之外的两条不同的直线,给出4个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中3个论断为条件,余下一个论断为结论,写出你认为正确的一个命题:________. 14.(10分) 如图K44-11,在长方体ABCD-A1B1C1D1中,DA=DC=2,DD1=,E是C1D1的中点,F是CE的中点. (1)求证:EA∥平面BDF; (2)求证:平面BDF⊥平面BCE. 图K44-11 15.(13分)如图K44-12,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,O为AC的中点,PO⊥平面ABCD,PO=2,M为PD的中点. (1)证明:PB∥平面ACM; (2)证明:AD⊥平面PAC. 图K44-12 16.(12分) 如图K44-13,在矩形ABCD中,AB=2AD,E为AB的中点,现将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCDE,F为线段A′D的中点. (1)证明:EF∥平面A′BC; (2)求直线A′C与平面A′DE所成角的正切值. 图K44-13 课时作业(四十四)B 【基础热身】 1.C [解析] 设m在平面α内的射影为n,当l⊥n,且与平面α无公共点时,l⊥m,l∥α. 2.B [解析] l⊥α,α∥β⇒l⊥β,又m⊂β,故l⊥m,反之当l⊥m时,α,β的位置不确定.故选B. 3.B [解析] A显然不对,C、D中的直线l有可能在平面α内.故选B. 4.a [解析] 如图,取BC中点E,连接ED、AE, ∵AB=AC,∴AE⊥BC. ∵平面ABC⊥平面BDC, ∴AE⊥平面BCD, ∴AE⊥ED. 在Rt△ABC和Rt△BCD中, AE=DE=BC=a, ∴AD==a. 【能力提升】 5.D [解析] 只有选项D,a⊥β,α∥β⇒a⊥α. 6.B [解析] 当α⊥β时,平面α内的直线不一定垂直于平面β. 7.D [解析] 如图所示, 连接正方形ABCD的两条对角线AC、BD,交于点O,则BD⊥AC,又PA⊥平面ABCD,所以BD⊥PA,所以BD⊥平面PAO,则PO⊥BD,即PO是P到BD的距离.在△PAO中,∠PAO=90°,PA=12,AO=AC=6,所以PO===6. 8.C [解析] 如图所示, PA⊥PB,PA⊥PC,所以PA⊥平面PBC,所以PA⊥BC,又PH⊥平面ABC,所以AE⊥BC.即H是△ABC高的交点,所以H一定是△ABC的垂心. 9.A [解析] 在正方形中,DA⊥EA,DC⊥FC,∴在折叠后的四面体P-DEF中有DP⊥EP,DP⊥FP,又EP∩FP=P,∴DP⊥平面PEF. 10.4 [解析] 由题中图与已知得直角三角形有:△PAC、△PAB、△ABC、△PBC. 11. [解析] 如图, ∠C1OC是二面角C1-BD-C的平面角. 在Rt△C1OC中,tan∠C1OC=. 12.③ [解析] 因为AB=CB,E是AC的中点,所以BE⊥AC,同理有DE⊥AC,又BE∩DE=E,所以AC⊥平面BDE.因为AC⊂平面ABC,所以平面ABC⊥平面BDE.又由于AC⊂平面ACD,所以平面ACD⊥平面BDE.故只有③正确. 13.②③④⇒①或①③④⇒② [解析] 由题意可构造出四个命题(1)①②③⇒④;(2)①②④⇒③;(3)①③④⇒②;(4)②③④⇒①.只有(3)(4)是正确的. 14.[解答] 证明:(1)连接AC交BD于O点,连接OF, 可得OF是△ACE的中位线,OF∥AE. 又AE⊄平面BDF,OF⊂平面BDF, 所以EA∥平面BDF. (2)计算可得DE=DC=2,又F是CE的中点, 所以DF⊥CE. 又BC⊥平面CDD1C1, 所以DF⊥BC. 又BC∩CE=C, 所以DF⊥平面BCE. 又DF⊂平面BDF, 所以平面BDF⊥平面BCE. 15.[解答] (1)证明:连接BD,MO.在平行四边形ABCD中,因为O为AC的中点,所以O为BD的中点.又M为PD的中点,所以PB∥MO.因为PB⊄平面ACM,MO⊂平面ACM,所以PB∥平面ACM. (2)证明:因为∠ADC=45°,且AD=AC=1,所以∠DAC=90°,即AD⊥AC.又PO⊥平面ABCD,AD⊂平面ABCD,所以PO⊥AD.而AC∩PO=O,所以AD⊥平面PAC. 【难点突破】 16.[解答] (1)证明:取A′C的中点M,连接MF,MB, 则FM∥DC,且FM=DC, 又EB∥DC,且EB=DC, 从而有FM綊EB, 所以四边形EBMF为平行四边形, 故有EF∥MB. 又EF⊄平面A′BC,MB⊂平面A′BC, 所以EF∥平面A′BC. (2)连接CE,则CE⊥DE,因为平面A′DE⊥平面BCDE,且交线为DE, 所以CE⊥平面A′DE,A′C在平面A′DE上的射影为A′E. 所以∠CA′E是直线A′C与平面A′DE所成角. 因为在矩形ABCD中,AB=2AD, 设AD=a, 则AB=2a,CE=a. 又A′E=a,所以tan∠CA′E===, 故直线A′C与平面A′DE所成角的正切值为. 查看更多