2018届二轮复习选择题压轴题突破课件（全国通用）

2018届二轮复习选择题压轴题突破课件（全国通用）

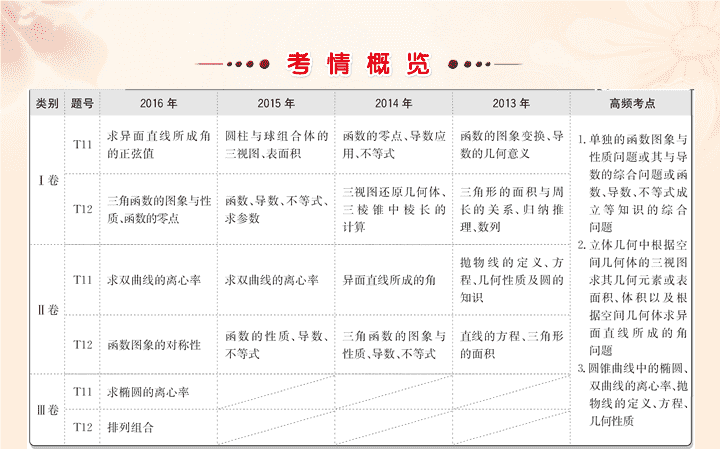
第二部分 冲刺名校专项突破 第一讲 选择题压轴题突破 压轴热点一 　立体几何中的三视图、表面积、体积、接切问题及异面直线所成角问题 【 典例 1】 (2015 · 全国卷 Ⅰ) 圆柱被一个平面截去一部 分后与半球 ( 半径为 r) 组成一个几何体，该几何体三视 图中的正视图和俯视图如图所示 ① . 若该几何体的 表面 积为 16+20π ② ，则 r=( 　　 ) A.1 B.2 C.4 D.8 【 信息联想 】 信息①：看到几何体的正视图和俯视图，想到还原该几何体 . 信息②：看到表面积，想到利用表面积公式求解 . 【 解题流程 】 选 B. 第一步：还原几何体 . 由正视图和俯视图知，该几何体是半球与半个圆柱的组合体 . 第二步：利用表面积公式列方程求解 . 圆柱的底面半径与球的半径都为 r ，圆柱的高为 2r ，其 表面积为 ×4πr 2 +πr×2r+πr 2 +2r×2r=5πr 2 +4r 2 = 16+20π ，解得 r=2. 【 规律方法 】 1. 由三视图还原直观图的关键：弄清几何体的形状、数量特征与三视图的关系 . 2. 求解几何体的面积及体积问题的技巧 (1) 求三棱锥的体积，常用等体积转化法 . (2) 求不规则几何体的体积，常用分割或补形法 . (3) 求面积问题，关键是空间问题平面化及熟记常用公式 . 3. 解决空间几何体间接切问题的关键：作平面将空间几何体间的接切，转化为平面图形间的接切 . 4. 求异面直线所成角的方法：常用 “ 平移直线法 ” . 【 押题预测 】 1. 一个几何体的三视图及尺寸如图所示 , 则该几何体的外接球半径为　 ( 　　 ) 【 解析 】 选 D. 如图所示 , 直观图为三棱锥 P - ABC, AB ⊥ BC, 平面 PAC ⊥ 平面 ABC, 过 P 作 PD⊥AC 于 D, 则 D 是 AC 的中点 ,PD⊥ 平面 ABC, 则外接球球心 O 在线段 PD 上 . 由三视图得 PD= =4, AC=6 . 设外接球的半径为 r, 在直角三角形 ODC 中 , 由 OD 2 =OC 2 -CD 2 , 得 (4-r) 2 =r 2 -(3 ) 2 , 解得 r= 2. 在正方体 ABCD-A′B′C′D′ 中 , 点 P 在线段 AD′ 上 运动 , 则异面直线 CP 与 BA′ 所成的角 θ 的取值范围是 　 ( 　　 ) 【 解析 】 选 D. 如图 , 连接 CD ′ , 则异面直线 CP 与 BA′ 所成的角 θ 等于∠ D′CP, 由图可知 , 当 P 点与 A 点重合时 ,θ= , 当 P 点无限接近 D′ 点时 ,θ 趋近于 0, 由于是异面直线 , 故 θ≠0, 所以角 θ 的取值范围是 0<θ≤ . 压轴热点二 　函数的图象与性质问题或其与导数、不等 式等的综合问题 【 典例 2】 (2016· 全国卷 Ⅱ) 已知函数 f(x)(x∈R ) 满足 f(-x )=2-f(x) ，若函数 y= ① 与 y= f(x ) 图象的交点为 (x 1 ， y 1 ) ， (x 2 ， y 2 ) ， … ， ( x m ， y m ) ，则 ② = ( 　　 ) A.0 B.m C.2m D.4m 【 信息联想 】 信息①：看到 f(-x )=2-f(x) 及 y= ，想到 f(x ) 与 y= 的图象都关于点 (0 ， 1) 对称 . 信息②：看到图象的交点，想到 f(x ) 与 y= 图象的 对称性，它们的交点成对出现，且其横坐标之和为 0 ， 纵坐标之和为 2. 【 解题流程 】 选 B. 第一步：确定 f(x ) 与 y= 的对称性 . 由 f(-x )=2-f(x) ，得 f(x ) 的图象关于 (0 ， 1) 对称，而 y= +1 ，也关于 (0 ， 1) 对称 . 第二步：判断交点的对称性及性质 . 由于 y= f(x ) 与 y= 都关于 (0 ， 1) 对称，故它们的交 点成对出现，其横坐标之和为 0 ，纵坐标之和为 2 ，这 样的交点共 对 . 第三步：求 综上所述， =0+2 · =m. 【 规律方法 】 1. 求解函数的图象与性质综合应用问题的策略 (1) 熟练掌握图象的变换法则及利用图象解决函数性质、方程、不等式问题的方法 . (2) 熟练掌握确定与应用函数单调性、奇偶性、周期性、最值、对称性及零点的方法 . 2. 利用导数解决不等式问题的思路 (1) 构造函数法：解决不等式恒成立问题，常利用构造函数法，然后利用导数知识解决 . 常见的构造函数的方法有移项法、构造形似函数法、主元法、放缩法等 . (2) 变量分离法：是将不等式 f(x )>0 作变形，将参数 a 和变量 x 进行分离，将不等式转化为 h(a )> g(x )( 或 h(a )< g(x )) 求解 . 【 押题预测 】 1. 已知函数 f(x )= 的图象上关于 y 轴 对称的点至少有 3 对 , 则实数 a 的取值范围是　 ( 　　 ) 【 解析 】 选 A.f(x )= 令 φ (x )=sin -1(x<0), 则 φ (x ) 关于 y 轴对称的函数为 g(x )=-sin -1(x>0), 则函数 f(x ) 的图象上关于 y 轴对称的点至少有 3 对 , 即函数 g(x ) 的图象与函数 h(x )= log a x(a >0,a≠1) 的图 象至少有 3 个交点 ( 如图所示 ), 2. 已知函数 f(x )= -2lnx(a∈R) ， g(x )=- ，若 至少存在一个 x 0 ∈[1 ， e] ，使 f(x 0 )>g(x 0 ) 成立，则实 数 a 的范围为 ( 　　 ) 【 解析 】 选 B. 由题意知， f(x)-g(x )>0 在 [1 ， e] 上有 解，即 ax-2lnx>0 ， a> 设 y= 则 y′= 因此当 x=1 时， =0 ，所以 a>0. 压轴热点三 　椭圆、双曲线的几何性质及抛物线的定 义、几何性质 【 典例 3】 (2016· 全国卷 Ⅱ) 已知 F 1 ， F 2 是双曲线 E ： 的左、右焦点， 点 M 在 E 上， ① MF 1 与 x 轴垂直 ② ， sin∠MF 2 F 1 = ，则 E 的离心率为 ( 　　 ) 【 信息联想 】 信息①：看到 M 在 E 上，想到可设 M(x ， y) ，且 M 适合双 曲线 E 的方程，得到坐标 x ， y 满足的关系式 . 信息②：看到 MF 1 与 x 轴垂直，想到 M(x ， y) 中 x=-c ， △ MF 1 F 2 为直角三角形 . 且 sin∠MF 2 F 1 = 得到 a ， b ， c 的关系 . 【 解题流程 】 选 A. 第一步：求出 M 点坐标 . 如图所示，设 M(-c ， y) ，则 所以 y= 第二步，将 sin∠MF 2 F 1 用 a ， b ， c 表示，并由 sin∠MF 2 F 1 = 得到 a ， b ， c 的关系 . 在 Rt△MF 2 F 1 中， 所以 a=b. 第三步：求离心率大小 . 【 规律方法 】 求椭圆、双曲线离心率大小 ( 范围 ) 的方法 根据已知椭圆、双曲线满足的几何条件及性质得到参数 a ， b ， c 满足的等量关系 ( 不等关系 ) ，然后把 b 用 a ， c 表 示，求 的值 ( 范围 ). 【 押题预测 】 1. 已知双曲线 C ： (a ， b>0) 的左、右焦点分别 为 F 1 ， F 2 ，过 F 2 的直线与双曲线 C 的右支相交于 P ， Q 两 点，若 PQ⊥PF 1 ，且 |PF 1 |=|PQ| ，则双曲线的离心率 e =( 　　 ) 【 解析 】 选 D. 设 |PF 2 |=m ， |QF 2 |=n ， 则由题意得 |PF 1 |=|PQ|= m+n ， |QF 1 |= 则 解得 又因为 |PF 1 | 2 +|PF 2 | 2 =|F 1 F 2 | 2 ， 即 [(2 -2)a+2a] 2 +[(2 -2)a] 2 =(2c) 2 ， 解得 则双曲线的离心率 2. 如图，等腰梯形 ABCD 中， AB∥CD 且 AB=2 ， AD=1 ， DC=2x(x∈(0 ， 1)). 以 A ， B 为焦点，且过点 D 的双曲线的离心率为 e 1 ，以 C ， D 为焦点，且过点 A 的椭圆的离心率为 e 2 ，则 e 1 +e 2 的取值范围为 ( 　　 ) 【 解析 】 选 B. 由已知得 |DB|= 由双曲线定义和椭圆定义得 a 1 = c 1 =1 ， a 2 = c 2 =x ， 则： 设 -1=t(0f( -1)= ， 得 e 1 +e 2 ∈( ， +∞).