- 2021-06-10 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学文(平行班)卷·2019届陕西省西安中学高二上学期期中考试(2017-11)
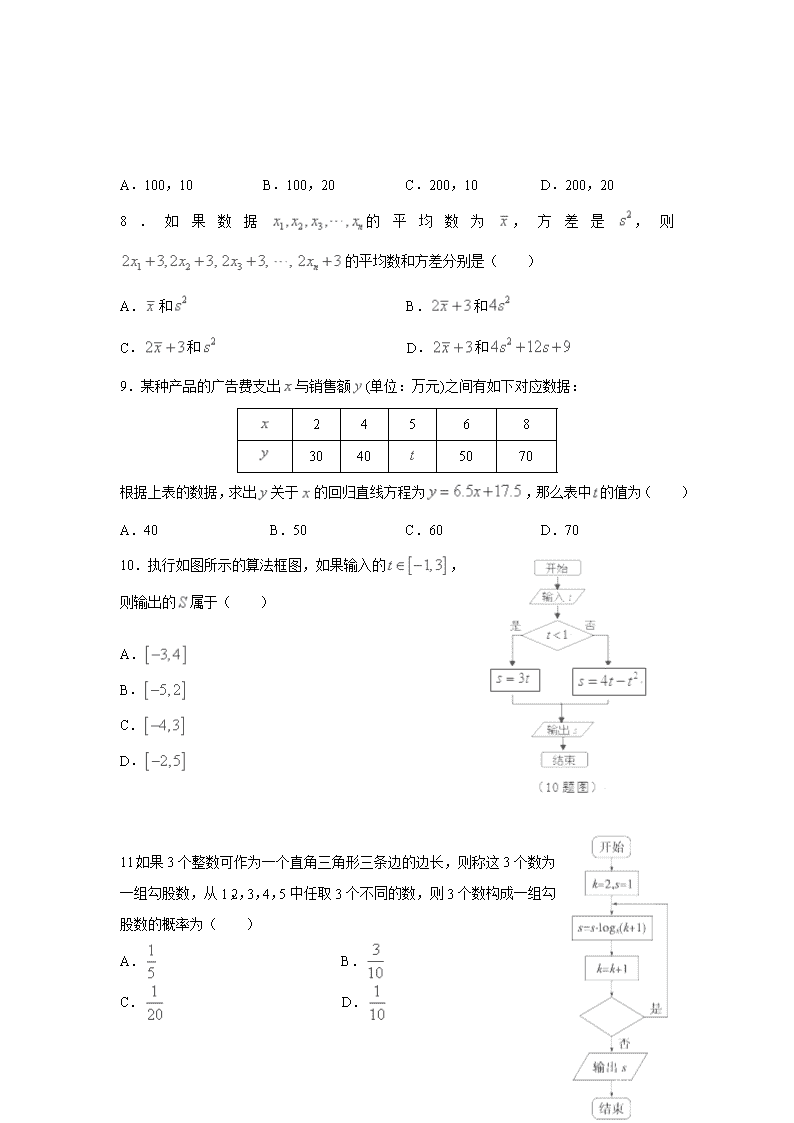
小二黑体 西安中学2017-2018学年度第一学期期中考试 高二数学(文科普通班)试题 (时间:120分钟 满分:150分) 命题人: 一、选择题:(本题共12小题,每题5分,共60分.每题有且只有一个正确答案, 直接将答案填写在指定位置) 1.为了解1200名学生对学校教改试验的意见,打算从中抽取一个容量为30的样本,考虑采用系统抽样,则分段的间隔为( ) A.40 B.30 C.20 D.12 2.命题“存在实数,使”的否定是( ) A.对任意实数,都有 B.不存在实数,使 C.对任意实数,都有 D.存在实数,使 3.已知命题p:若,则;命题q:若,则.在命题①p且q;②p或q;③p且();④()或q中,真命题是( ) A.①③ B.②③ C.①④ D.②④ 4.椭圆的焦距为4,则等于( ) A.4 B.8 C.4或8 D.12 5.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的 两个事件是( ) A.至少有1个白球,都是白球 B.恰有1个白球,恰有2个白球 C.至少有1个白球,至少有1个红球 D.至少有1个白球,都是红球 6.丁大姐常说“便宜没好货”,她这句话的意思是:“好货”是“不便宜”的( ) A.充分条件 B.必要条件 C.充分必要条件 D.既非充分又非必要条件 7.已知某地区中小学生人数和近视情况分别如图1和图2所示,为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别是( ) 小学生 3500名 初中生 4500名 高中生 2000名 A.100,10 B.100,20 C.200,10 D.200,20 8.如果数据的平均数为,方差是,则的平均数和方差分别是( ) A.和 B.和 C.和 D.和 9.某种产品的广告费支出与销售额(单位:万元)之间有如下对应数据: 2 4 5 6 8 30 40 50 70 根据上表的数据,求出关于的回归直线方程为,那么表中的值为( ) A.40 B.50 C.60 D.70 10.执行如图所示的算法框图,如果输入的, 则输出的属于( ) A. B. C. D. 11.如果3个整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则3个数构成一组勾股数的概率为( ) A. B. C. D. 12.执行如图所示的算法框图,如果输出,那么判断框内应填入的条件是( ) A. B. (12题图) C. D. 二、填空题:(本题共4小题,每题5分,共20分, 直接将答案填写在指定位置) 13.某校高一年级有900名学生,其中女生400名,按男女比例用分层抽样的方法,从该年级学生中抽取一个容量为45的样本,则应抽取的男生人数为________. 14.甲乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为________. 15.顾客请一位工艺师把、两件玉石原料各制成一件工艺品,工艺师带一位徒弟完成这项任务,每件原料先由徒弟完成粗加工,再由工艺师进行精加工完成制作,两件工艺品都完成后交付顾客,两件原料每道工序所需时间(单位:工作日)如下: 工序 时间 原料 粗加工 精加工 原料 原料 则最短交货期为 个工作日. 16.在区间和上分别各取一个数,记为和,则方程表示焦点在轴上的椭圆的概率是____________. 三、解答题:(本题共6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤,在答题卷中相应位置作答) 17.(本小题满分10分)已知命题:任意;命题:存在, ;若“且”为假命题,“或”为真命题,求实数的取值范围. 18.(本小题满分12分)某车间20名工人年龄数据如下表: 年龄(岁) 工人数(人) 19 1 28 3 29 3 30 5 31 4 32 3 40 1 合计 20 (1)求这20名工人年龄的众数与极差; (2)以这十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图; (3)求这20名工人年龄的方差. 19.(本小题满分12分)求满足下列条件的椭圆的标准方程: (1)两个焦点坐标分别是,,椭圆上一点到两焦点的距离之和等于10; (2)过点,且与椭圆有相同的焦点. 20.(本小题满分12分)现有分别写有1,2,3,4,5的5张卡片. (1)从中随机抽取2张,求两张卡片上数字和为5的概率; (2)从中随机抽取1张,放回后再随机抽取1张,求抽得的第一张卡片上的数大于第二张卡片上的数的概率. 21.(本小题满分12分)随着移动互联的快速发展,基于互联的共享单车应运而生.某市场研究人员为了了解共享单车运营公司的经营状况,对该公司最近六个月(2017年5月到2017年10月)内在西安市的市场占有率进行了统计,并绘制了相应的拆线图. (1)由拆线图可以看出,可用线性回归模型拟合月度市场占有率与月份代码之间的关系.求关于的线性回归方程; (2)公司对员工承诺如果公司的共享单车在2017年年底(12月底)能达到西安市场占有率的,员工每人都可以获得年终奖,依据上面计算得到回归方程估计员工是否能得到年终奖. (参考公式:回归直线方程为,其中) 22.(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表: 质量指标值分组 [75,85) [85,95) [95,105) [105,115) [115,125) 频数 6 26 38 22 8 (1)在答题卡上画出这些数据的频率分布直方图(要求用阴影部分显示); (2)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定? (3)估计这种产品质量指标值的平均值及中位数(其中求平均值时同一组中的数据用该组区间的中点值作代表,求中位数精确到0.1).查看更多