- 2021-06-10 发布 |
- 37.5 KB |
- 6页

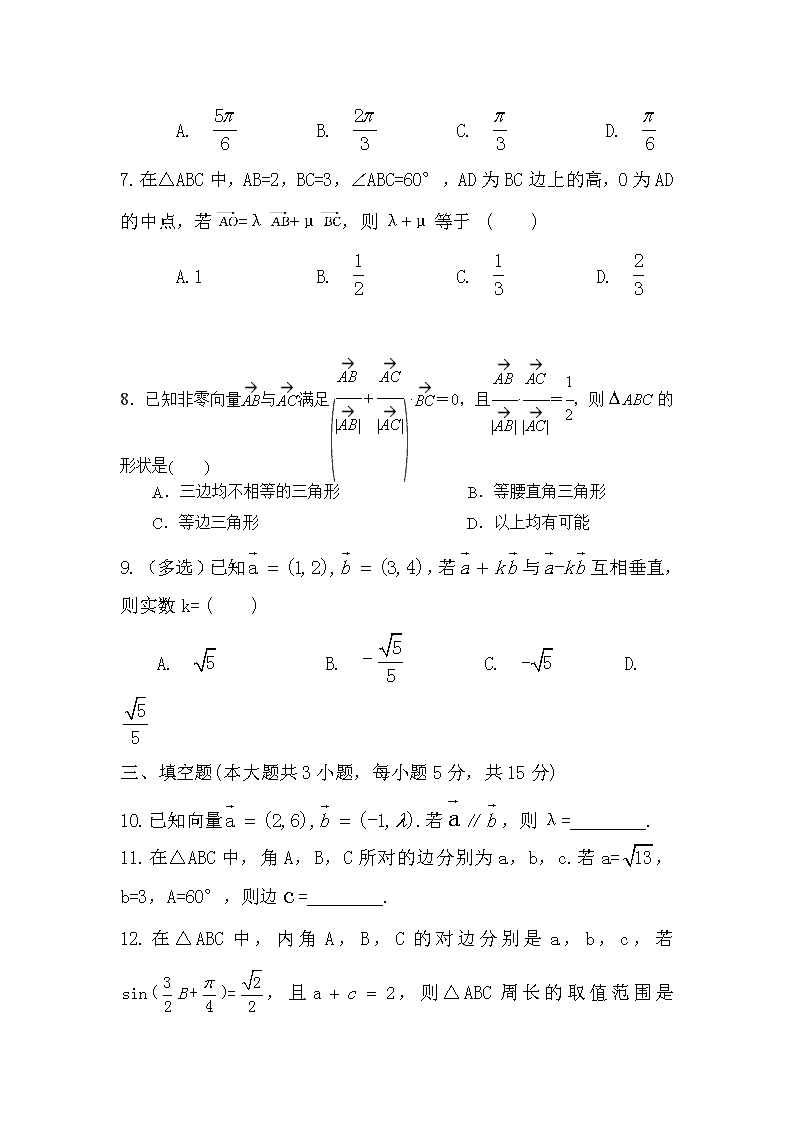

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019-2020学年山东省枣庄市第八中学东校区高一3月月考(网络测试)数学试题
高一数学必修二模块素养评价 (时间100分钟 ,满分100分) 2020.3.1 一、选择题(本大题共8小题,每小题5分,共45分 1.已知平面向量,则向量 ( ) A.(-2,-1) B.(-2,1) C.(-1,0) D.(-1,2) 2. 计算(1+i)(2+i)= ( ) A.1-i B.1+3i C.3+i D.3+3i 3.复平面内表示复数z=i(-2+i)的点位于 ( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 4.设i是虚数单位,复数是纯虚数,则实数= ( ) A.2 B. C. D.-2 5.在△ABC中,A=,BC=3,AB=,则C等于 ( ) A. B. C. D. 6.已知向量满足,,则的夹角θ等于( ) A. B. C. D. 7.在△ABC中,AB=2,BC=3,∠ABC=60°,AD为BC边上的高,O为AD的中点,若=λ+μ,则λ+μ等于 ( ) A.1 B. C. D. 8.已知非零向量与满足·=0,且·=,则ABC的形状是( ) A.三边均不相等的三角形 B.等腰直角三角形 C.等边三角形 D.以上均有可能 9.(多选)已知,若与互相垂直,则实数k= ( ) A. B. C. D. 三、填空题(本大题共3小题,每小题5分,共15分) 10.已知向量.若∥,则λ=________. 11.在△ABC中,角A,B,C所对的边分别为a,b,c.若a=,b=3,A=60°,则边=________. 12.在△ABC中,内角A,B,C的对边分别是a,b,c,若,且,则△ABC周长的取值范围是 ________. 四、解答题(本大题共2小题,共40分. 13.(20分)△ABC的内角A,B,C的对边分别为a,b,c,已知. (1)求cos B; (2)若,△ABC的面积为2,求b. 14.(20分)已知在△ABC中,角A,B,C的对边分别为a,b,c,向量=(sin A,sin B),=(cos B,cos A),=sin2C. (1)求角C的大小. (2)若,且·(-)=18,求边c的长. 高一数学单元检测参考答案 2020.3.1 1. 【解析】选D.因为a=(1,1),b=(1,-1), 所以a-b=(1,1)-(1,-1) =-=(-1,2). 2. 【解析】选B.依题意得(1+i)(2+i)=2+i2+3i=1+3i. 3.【解析】选C.z=i(-2+i)=-2i+i2=-1-2i,故复平面内表示复数z=i(-2+i) 的点(-1,-2)位于第三象限. 4. 【解析】选B.因为= =是纯虚数, 所以2a-1=0且a+2≠0,所以a=. 5.【解析】选C.BC=a=3,AB=c=,由正弦定理,得sin C==,又a=3,c=,所以a>c,即A>C,故C为锐角.所以C=. 6.【解析】选B.由|b-a|=可得b2-2a·b+a2=16-2a·b+25=61,所以a·b=-10,所以cos θ==-=-,所以θ=120°. 7.【解析】选D.因为=+=+, 所以2=+,即=+. 故λ+μ=+=. 8.解析 答案 C ∵·=0,∴∠A的平分线所在的向量与垂直,所以△ABC为等腰三角形.又·=,∴cosA=,∴∠A=.故△ABC为等边三角形. 9. 【解析】选BD.由已知a=(1,2),b=(3,4),若a+kb与a-kb互相垂直,则(a+kb)·(a-kb)=0,即a2-k2b2=0,即5-25k2=0,即k2=,所以k=±. 10. 【解析】因为a∥b,所以-1×6=2λ,所以λ=-3. 答案:-3 11.【解析】a2=c2+b2-2cbcos A⇒13=c2+9-2c×3×cos 60°,即c2-3c-4=0,解得c=4或c=-1(舍去). 答案:4 12.【解析】因为sin=,且角B为三角形的内角,所以B=,所以B=.又b2=a2+c2-2accos B=(a+c)2-3ac=4-3ac≥4-=1,当且仅当a=c=1时,取等号,所以b≥1,所以a+c+b≥3;又a+c=2>b,所以a+c+b<4,所以△ABC周长的取值范围是[3, 4). 答案:[3,4) 13.【解析】(1)由题设及A+B+C=π得sin(A+C)=sin B=8sin2,故sin B=4(1-cos B),上式两边平方,整理得17cos2B-32cos B+15=0, 解得cos B=1(舍去),cos B=. (2)由cos B=得sin B=, 故S△ABC=acsin B=ac,又S△ABC=2, 则ac=, 由余弦定理及a+c=6得b2=a2+c2-2accos B=(a+c)2-2ac(1+cos B)= 36-2××=4,所以b=2. 14.【解析】(1)m·n=sin A·cos B+sin B·cos A =sin(A+B),对于△ABC,A+B=π-C,0查看更多
- 当前文档收益归属上传用户