用样本的频率分布估计总体分布1

用样本的频率分布估计总体分布1

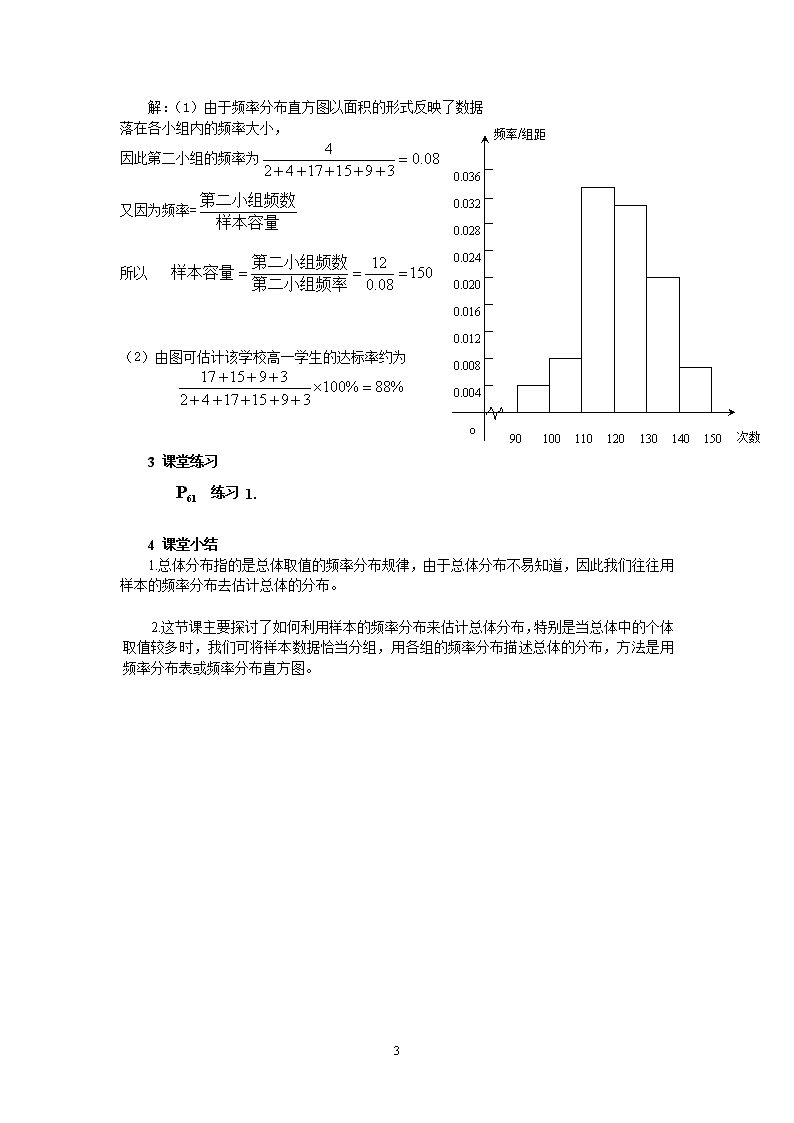
‎ ‎ ‎§２.2.1用样本的频率分布估计总体分布 教材：普通高中课程标准实验教科书(A版)数学必修3‎ 一、教学目的 ‎（1） 通过实例体会分布的意义和作用。‎ ‎（2）在表示样本数据的过程中，学会列频率分布表，画频率分布直方图、频率分布折线图。‎ ‎（3）通过实例体会频率分布直方图、频率折线图的特征，从而恰当地选择上述方法分析样本的分布，准确地做出总体估计。‎ 二、重点与难点 重点：会列频率分布表，画频率分布直方图、频率折线图。‎ 难点：能通过样本的频率分布估计总体的分布。‎ 三、教学过程 ‎1.创设情景，引入新课〖探究〗：P55‎ 我国是世界上严重缺水的国家之一，城市缺水问题较为突出，某市政府为了节约生活用水，计划在本市试行居民生活用水定额管理，即确定一个居民月用水量标准a，用水量不超过a的部分按平价收费，超出a的部分按议价收费。如果希望大部分居民的日常生活不受影响，那么标准a定为多少比较合理呢 ？你认为，为了了较为合理地确定出这个标准，需要做哪些工作？（让学生展开讨论）‎ ‎2讲授新课 为了制定一个较为合理的标准a，必须先了解全市居民日常用水量的分布情况，比如月均用水量在哪个范围的居民最多，他们占全市居民的百分比情况等。因此采用抽样调查的方式，通过分析样本数据来估计全市居民用水量的分布情况。（如课本P56）‎ ‎2.1分析数据一些常见的方法 分析数据的一种基本方法是用图将它们画出来，或者用紧凑的表格改变数据的排列方式，作图可以达到两个目的，一是从数据中提取信息，二是利用图形传递信息。表格则是通过改变数据的构成形式，为我们提供解释数据的新方式。‎ 下面我们学习的频率分布表和频率分布图，则是从各个小组数据在样本容量中所占比例大小的角度，来表示数据分布的规律。可以让我们更清楚的看到整个样本数据的频率分布情况。‎ ‎2.2频率分布的概念以及画频率分布直方图的一般步骤 频率分布是指一个样本数据在各个小范围内所占比例的大小。一般用频率分布直方图反映样本的频率分布。‎ 画频率分布直方图的一般步骤：‎ （1） 求极差即计算一组数据中最大值与最小值的差 例如：在上述问题中极差应该是4.3-0.2=4.1.说明了样本数据的变化范围是4.1t ‎（2）组距与组数 ‎ 组距与组数的确定没有固定的标准，常常要一个尝试和选择的过程。将数据分组时，组数应力求合适，当然数据分组与样本容量有关，一般样本容量越大，所分组数就越多。一般情况下，当样本容量不超过100时，一般分成5—12组。‎ 组数=极差/组距 ‎（3）数据分组 3‎ ‎ ‎ 决定分点，分组时应保证将样本数据落在每一组的内部。我们通常的做法是将分点数比数据多一位小数或把第一组的起点稍减小一点。‎ ‎(4)列频率分布表 ‎(5)画频率分布直方图 画图时，应以横轴表示月均用水量，纵轴表示频率与组距的比值。再以每个组距为底，以各频率除以组距的商为高，分别画出矩形，这样得到的直方图就是频率分布直方图。‎ 在图中每个小矩形的面积表示了相应各组的频率。它反映了数据落在各个小组频率的大小，在频率分布直方图中，各个小矩形的面积之和等于1。‎ 以课本P56制定居民用水标准问题为例，经过以上几个步骤画出频率分布直方图。（利用多媒体演示）‎ 频率分布直方图的特征：‎ ‎(1)从频率分布直方图可以清楚的看出数据分布的总体趋势。‎ ‎(2)从频率分布直方图得不出原始的数据内容，把数据表示成直方图后，原有的具体数据信息就被抹掉了。‎ ‎2.3〖探究〗P58:同样一组数据，如果组距不同，横轴、纵轴的单位不同，得到的图和形状也会不同。不同的形状给人以不同的印象，这种印象有时会影响我们对总体的判断，分别以0.1和1为组距重新作图，然后谈谈你对图的印象？（把学生分成两大组进行，分别作出两种组距的图，然后组织同学们对所作图不同的看法进行交流……）（老师用多媒体演示）‎ 接下来请同学们思考下面这个问题：‎ ‎〖思考〗：如果当地政府希望使85%以上的居民每月的用水量不超出标准，根据频率分布表2-2和频率分布直方图2.2-1，（见课本P57）你能对制定月用水量标准提出建议吗？（让学生仔细观察表和图）‎ ‎2.4频率分布折线图、总体密度曲线 ‎2.4.1频率分布折线图的定义：‎ 连接频率分布直方图中各小长方形上端的中点，就得到频率分布折线图。‎ ‎2.4.2总体密度曲线的定义：‎ 在样本频率分布直方图中，相应的频率折线图会越来越接近于一条光滑曲线，统计中称这条光滑曲线为总体密度曲线。它能够精确地反映了总体在各个范围内取值的百分比，它能给我们提供更加精细的信息。（见课本P60）‎ ‎〖思考〗：‎ ‎１．对于任何一个总体，它的密度曲线是不是一定存在？为什么？‎ ‎２．对于任何一个总体，它的密度曲线是否可以被非常准确地画出来？为什么？‎ 实际上，尽管有些总体密度曲线是饿、客观存在的，但一般很难想函数图象那样准确地画出来，我们只能用样本的频率分布对它进行估计，一般来说，样本容量越大，这种估计就越精确．‎ ‎3.【例题精析】‎ ‎〖例〗：为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数次测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12.‎ ‎（1）第二小组的频率是多少？样本容量是多少？‎ ‎（2）若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？‎ 分析：在频率分布直方图中，各小长方形的面积等于相应各组的频率，小长方形的高与频数成正比，各组频数之和等于样本容量，频率之和等于1。‎ 3‎ ‎ ‎ 解：（1）由于频率分布直方图以面积的形式反映了数据 ‎90‎ ‎100‎ ‎110‎ ‎120‎ ‎130‎ ‎140‎ ‎150‎ 次数 o ‎0.004‎ ‎0.008‎ ‎0.012‎ ‎0.016‎ ‎0.020‎ ‎0.024‎ ‎0.028‎ 频率/组距 ‎0.032‎ ‎0.036‎ 落在各小组内的频率大小，‎ 因此第二小组的频率为 又因为频率=‎ 所以 ‎ ‎ ‎ ‎（2）由图可估计该学校高一学生的达标率约为 ‎3 课堂练习 P61 练习 1. ‎ ‎4 课堂小结 ‎1.总体分布指的是总体取值的频率分布规律，由于总体分布不易知道，因此我们往往用样本的频率分布去估计总体的分布。‎ ‎2.这节课主要探讨了如何利用样本的频率分布来估计总体分布，特别是当总体中的个体取值较多时，我们可将样本数据恰当分组，用各组的频率分布描述总体的分布，方法是用频率分布表或频率分布直方图。‎ 3‎