圆锥曲线的方程脑图讲义课件

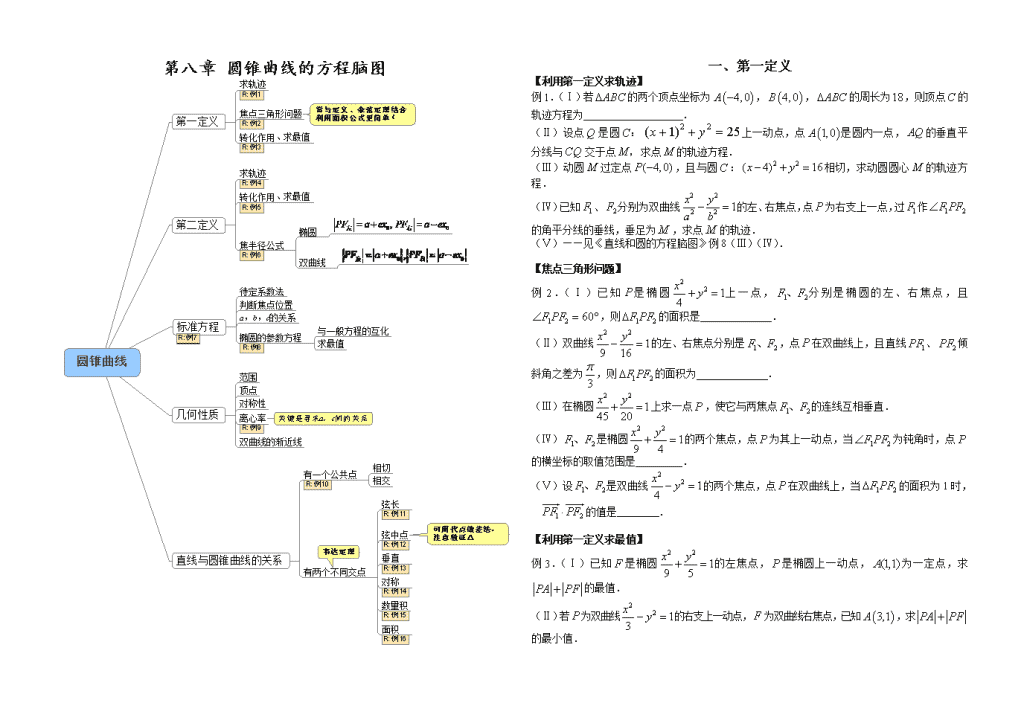
圆锥曲线的方程脑图讲义课件

第八章 圆锥曲线的方程脑图 一、第一定义 ‎【利用第一定义求轨迹】‎ 例1．（Ⅰ）若的两个顶点坐标为，，的周长为，则顶点的轨迹方程为 ．‎ ‎（Ⅱ）设点Q是圆C：上一动点，点是圆内一点，的垂直平分线与CQ交于点M，求点M的轨迹方程． ‎ ‎（Ⅲ）动圆过定点，且与圆：相切，求动圆圆心的轨迹方程．‎ ‎（Ⅳ）已知、分别为双曲线的左、右焦点，点为右支上一点，过作的角平分线的垂线，垂足为，求点的轨迹． ‎ ‎（Ⅴ）——见《直线和圆的方程脑图》例8（Ⅲ）（Ⅳ）．‎ ‎【焦点三角形问题】‎ 例2．（Ⅰ）已知是椭圆上一点，分别是椭圆的左、右焦点，且，则的面积是 ．‎ ‎（Ⅱ）双曲线的左、右焦点分别是，点在双曲线上，且直线、倾斜角之差为，则的面积为 ．‎ ‎（Ⅲ）在椭圆上求一点，使它与两焦点的连线互相垂直．‎ ‎（Ⅳ）是椭圆的两个焦点，点为其上一动点，当为钝角时，点的横坐标的取值范围是 ．‎ ‎（Ⅴ）设是双曲线的两个焦点，点在双曲线上，当的面积为1时，的值是 ．‎ ‎【利用第一定义求最值】‎ 例3．（Ⅰ）已知是椭圆的左焦点，是椭圆上一动点，为一定点，求的最值． ‎ ‎（Ⅱ）若为双曲线的右支上一动点，为双曲线右焦点，已知，求的最小值． ‎ 二、第二定义 ‎【利用第二定义求轨迹】‎ 例4．（Ⅰ）已知动点满足，则点M的轨迹是 A．椭圆 B．双曲线 C．抛物线 D．两条相交直线 ‎（Ⅱ）已知圆：与定直线：，动圆和圆外切且与直线相切，求动圆的圆心的轨迹方程． ‎ ‎（Ⅲ）已知圆的方程为，动抛物线过点、，且以圆的切线为准线，求抛物线焦点的轨迹方程． ‎ ‎（Ⅳ）——见《直线和圆的方程脑图》例8（Ⅱ）、例9（Ⅱ）（Ⅸ）．‎ ‎【利用第二定义求最值】‎ 例5．（Ⅰ）已知是椭圆的左焦点，是椭圆上一动点，为一定点，求的最小值． ‎ ‎（Ⅱ）若为双曲线的右支上一动点，为双曲线右焦点，已知，求（1）的最小值． ‎ ‎（Ⅲ）若F为抛物线的焦点，点M在抛物线上移动，，求的最小值． ‎ ‎（Ⅳ）已知点P是抛物线= 2x上的动点，点P在y轴上的射影是M，点A的坐标是，则的最小值是 A． B．‎4 ‎‎ ‎ C． D．5‎ ‎【焦半径公式】‎ 例6．（Ⅰ）已知点在椭圆上，为椭圆的左右焦点，求的取值范围． ‎ ‎（Ⅱ）双曲线的两个焦点分别为，为双曲线上的任意一点，求证：、、成等比数列．‎ ‎（Ⅲ）已知抛物线的一条焦点弦被焦点分成为、的两部分，求证：．‎ ‎（Ⅳ）若双曲线，在右支上有一点，且到左焦点与到右焦点的距离之比为：，求点的横坐标． ‎ ‎（Ⅴ）在双曲线的一支上有不同的三点、，与焦点的距离成等差数列，求． ‎ 三、标准方程 ‎【待定系数法求圆锥曲线方程】‎ 例7．（Ⅰ）已知椭圆焦点在轴上，焦距等于4，并且经过点，求椭圆的标准方程．‎ ‎（Ⅱ）已知椭圆经过两点，，求椭圆的标准方程． ‎ ‎（Ⅲ）已知椭圆的长轴长是短轴长的2倍，且过点，求椭圆的标准方程．‎ ‎（Ⅳ）双曲线的一条准线是，则的值为 ．‎ ‎（Ⅴ）已知双曲线的右准线为，右焦点为，离心率，求双曲线方程．‎ ‎（Ⅵ）求与双曲线有共同的渐近线，且经过点的双曲线方程．‎ ‎（Ⅶ）求以椭圆的焦点为焦点，以直线为渐近线的双曲线的方程． ‎ ‎（Ⅷ）为何值时，方程表示①圆；②椭圆；③双曲线？‎ ‎（Ⅸ）抛物线的焦点坐标是 ．‎ ‎（Ⅹ）已知抛物线的准线为，求抛物线的标准方程． ‎ ‎（Ⅺ）已知抛物线的焦点在轴上，且到焦点的距离是，求抛物线的标准方程．‎ ‎（Ⅻ）已知抛物线焦点在轴上且截直线所得弦长为，求抛物线的标准方程．‎ ‎【利用椭圆的参数方程求最值】‎ 例8．已知实数、满足，①求的取值范围；②求的取值范围．‎ 四、几何性质 ‎【求离心率】‎ 例9．（Ⅰ）已知为椭圆的焦点，为椭圆上一点，垂直于轴，且，求离心率． ‎ ‎（Ⅱ）椭圆的左焦点为，，是两个顶点，如果到直线的距离是，求椭圆的离心率． ‎ ‎（Ⅲ）椭圆的两焦点为，以为边作正三角形，若椭圆恰好平分正三角形的两条边，则椭圆的离心率为 ．‎ ‎（Ⅳ）已知双曲线的两条渐近线方程是，求此双曲线的离心率．‎ ‎（Ⅴ）设双曲线的右焦点为，右准线与两条渐近线交于、两点，如果是直角三角形，则双曲线的离心率是 ．‎ ‎（Ⅵ）已知是椭圆的两个焦点，满足的点总在椭圆内部，求椭圆离心率的取值范围． ‎ ‎（Ⅶ）已知双曲线的右焦点为，若过点且倾斜角为的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是 A． B． C． D．‎ 五、直线与圆锥曲线的位置关系 ‎【有一个公共点】‎ 例10．（Ⅰ）已知椭圆，在椭圆上求一点，使到直线：的距离最小并求出最小值． ‎ ‎（Ⅱ）求经过点且与双曲线仅有一个公共点的直线方程．‎ ‎【有两个不同交点】——韦达定理 ‎【弦长】例11．（Ⅰ）抛物线截直线所得弦长等于 ．‎ ‎（Ⅱ）已知椭圆的中心在原点，焦点在坐标轴上，直线与该椭圆相交于和，且，，求椭圆方程． ‎ ‎【弦中点】例12．（Ⅰ）已知椭圆，①求斜率为2的平行弦的中点轨迹方程；②过的直线与椭圆相交，求被截得的弦的中点轨迹方程；③过点且被点平分的弦所在直线的方程． ‎ ‎（Ⅱ）已知双曲线，①过定点作直线交双曲线于点，使点是的中点，求此直线方程；②过定点能否作直线，使与双曲线相交于两点、，且是的中点？若存在，求出的方程；若不存在，说明理由．‎ ‎【垂直】例13．（Ⅰ）若直线：与双曲线交于、两点,且以为直径的圆过原点，求的值. ‎ ‎（Ⅱ）已知椭圆的中心在坐标原点，焦点在轴上，椭圆上的点到焦点距离的最大值为，最小值为．‎ ‎①求椭圆的标准方程； ‎ ‎②若直线与椭圆相交于，两点（、不是左右顶点），且以为直径的圆过椭圆的右顶点，求证：直线过定点，并求出该定点的坐标． ‎ ‎【对称】例14．（Ⅰ）已知椭圆的方程为，试确定的取值范围，使得对于直线，椭圆上有不同的两个点关于该直线对称． ‎ ‎（Ⅱ）已知抛物线上总存在关于直线对称的两点，则实数的取值范围是 ．‎ ‎【数量积】例15．已知中心在原点的双曲线的右焦点为，右顶点为，①求双曲线的方程；②若直线与双曲线有两个不同的交点和，且（为原点），求的取值范围． ‎ ‎【面积】例16．（Ⅰ）已知双曲线：的两个焦点为、，点在双曲线上．①求双曲线的方程；②记为坐标原点，过点的直线与双曲线相交于不同两点、，若的面积为，求直线的方程．‎ ‎（Ⅱ）已知中心在原点的双曲线的一个焦点是，一条渐近线的方程是．‎ ‎①求双曲线的方程；②若以为斜率的直线与双曲线相交于不同两点，且线段的垂直平分线与两坐标轴围成的三角形的面积为，求的取值范围．‎ 答案 一、第一定义 ‎【利用第一定义求轨迹】‎ 例1．（Ⅰ）．（Ⅱ）（Ⅲ）‎ ‎（Ⅳ）（Ⅴ）——见《直线和圆的方程脑图》例8（Ⅲ）（Ⅳ）．‎ ‎【焦点三角形问题】‎ 例2．（Ⅰ）．（Ⅱ）．（Ⅲ）‎ ‎（Ⅳ）．（Ⅴ）．‎ ‎【利用第一定义求最值】‎ 例3．（Ⅰ）,（Ⅱ）‎ 二、第二定义 ‎【利用第二定义求轨迹】‎ 例4．（Ⅰ）B（Ⅱ）（Ⅲ）‎ ‎（Ⅳ）——见《直线和圆的方程脑图》例8（Ⅱ）、例9（Ⅱ）（Ⅸ）．‎ ‎【利用第二定义求最值】‎ 例5．（Ⅰ）（Ⅱ）（Ⅲ）（Ⅳ）C ‎【焦半径公式】‎ 例6．（Ⅰ）（Ⅱ）证略（Ⅲ）证略（Ⅳ）（Ⅴ）‎ 三、标准方程 ‎【待定系数法求圆锥曲线方程】‎ 例7．（Ⅰ）（Ⅱ）（Ⅲ）或（Ⅳ）．‎ ‎（Ⅴ）（Ⅵ）或（Ⅶ）‎ ‎（Ⅷ）①②③（Ⅸ）．（Ⅹ） ‎ ‎（Ⅺ）或 （Ⅻ）或 ‎【利用椭圆的参数方程求最值】‎ 例8．①；②‎ 四、几何性质 ‎【求离心率】‎ 例9．（Ⅰ）（Ⅱ）（Ⅲ）．（Ⅳ）或（Ⅴ）．（Ⅵ）（Ⅶ）C 五、直线与圆锥曲线的位置关系 ‎【有一个公共点】‎ 例10．（Ⅰ），（Ⅱ），，和 ‎【有两个不同交点】——韦达定理 ‎【弦长】例11．（Ⅰ）．（Ⅱ）或 ‎【弦中点】例12．（Ⅰ）①②③‎ ‎（Ⅱ）①②不存在 ‎【垂直】例13．（Ⅰ）（Ⅱ）①②‎ ‎【对称】例14．（Ⅰ）（Ⅱ）．‎ ‎【数量积】例15．‎ ‎【面积】例16．（Ⅰ）①②‎ ‎（Ⅱ）①②‎