运动的合成和分解(3)

运动的合成和分解(3)

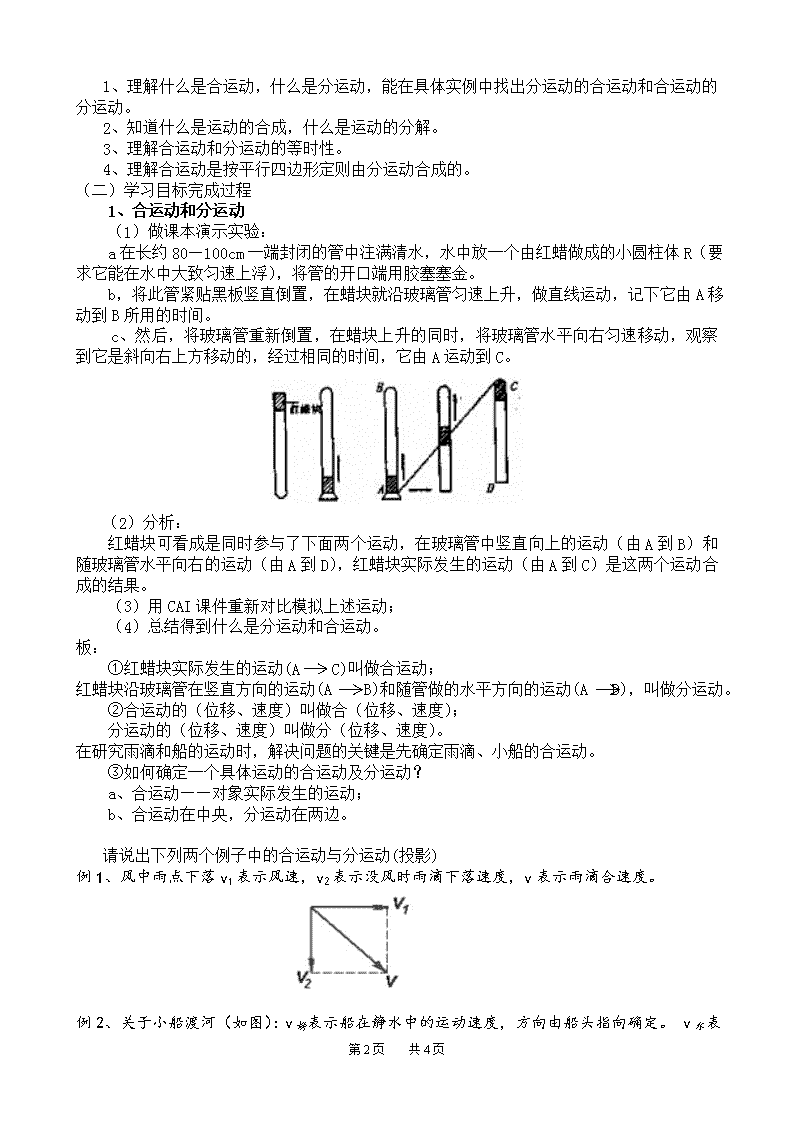
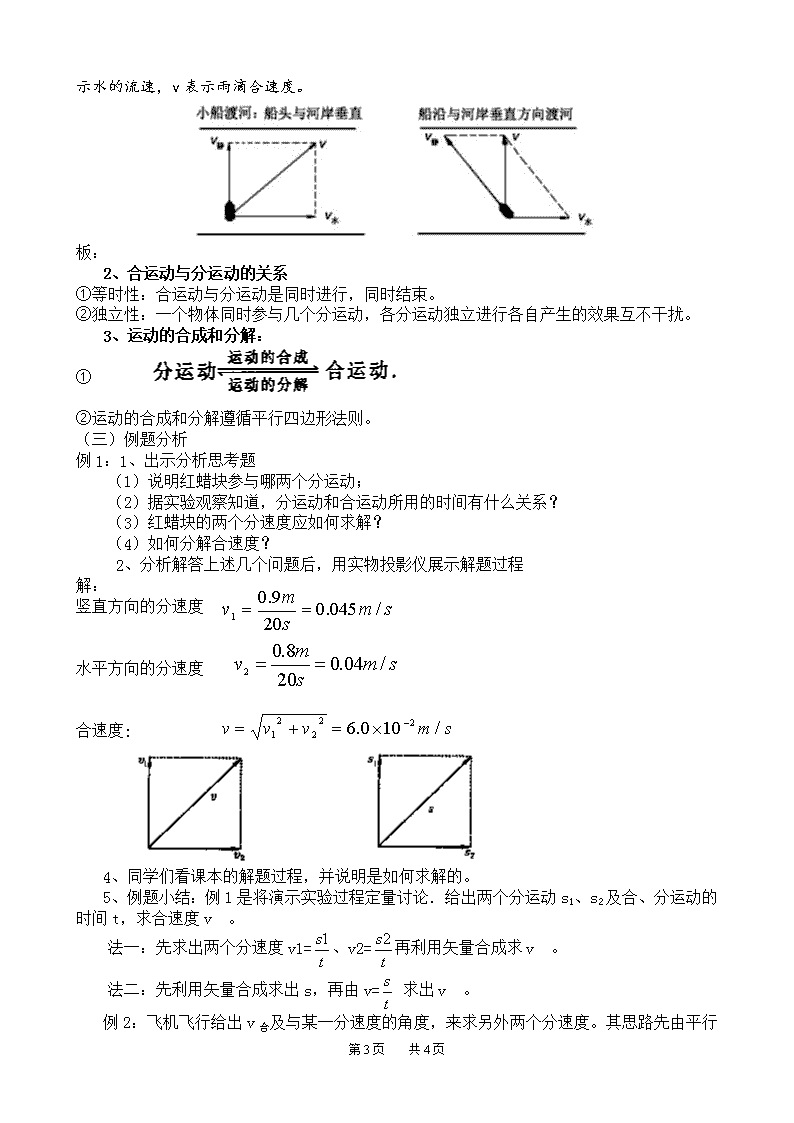
‎ ‎ 运动的合成和分解 一、教材分析：‎ ‎ “运动的合成和分解”是人教版高中《物理》第一册（必修）第五章“曲线运动”的第二节内容。在这一章中，教材的安排是第一节先讲述曲线运动的概念及物体做曲线运动的条件，本节讲述曲线运动的合成与分解。运动的合成与分解是研究较复杂运动的一种方法，即复杂的运动可以看作是几个较简单运动的合运动。这既是方法介绍又是研究平抛运动的预备知识。 ‎ 从整个高中物理教材的编排看，第一章中介绍了力的合成与分解的平行四边形定则，这一节是平行四边形定则在第二个矢量运算中的应用。学好这一节能使学生真正体会到平行四边形定则这一矢量运算法则，并且能很容易的推广到其它的矢量运算。‎ 矢量运算始终贯穿在高中物理知识内容的全过程中，因此无论从这一章看还是从整个教材看这一节是承上启下的重要知识。学好这节内容，一方面可以深化前面所学的知识，另一方面又为后续学习打好必要的基础。‎ 本节内容可分为四部分：演示实验、例题、对运动合成和分解轨迹的分析、思考与讨论，但都是围绕演示实验而展开的，层层深入，由提出问题到找出解决问题的方法，以至最后对运动合成和分解问题的进一步讨论。‎ 二、知识准备：‎ 学生已知道了什么是曲线运动；学生对平行四边形定则在力的运算中的应用已有深刻的认识；学生已具备了一定的分析能力。‎ 三、教学目标：‎ 知识目标：‎ ‎1、通过对多个具体运动的演示及分析，使学生明确什么是合运动，什么是分运动；合、分运动是同时发生的，并且不互相影响。‎ ‎2、知道什么是运动的合成，什么是运动的分解。理解运动的合成和分解遵循平行四边形定则。‎ ‎3、利用矢量合成的原理，解决运动合成和分解的具体情况，会用作图法、直角三角形的知识解决有关位移、速度合成和分解的问题。‎ 能力目标：‎ 培养学生应用数学知识解决物理问题的能力。‎ 情感目标：‎ 通过对运动合成与分解的练习和理解，发挥学生空间想象能力，提高对相关知识的综合应用能力。‎ 四、教学重点：‎ 对一个运动能正确地进行合成和分解。‎ 五、教学难点：‎ 具体问题中的合运动和分运动的判定。‎ 六、教学方法：‎ 训练法、推理归纳法、电教法、实验法、启发式、讨论法、反馈法 七、教学用具：‎ 投影仪、投影片、多媒体、CAI课件 八、教学程序设计： ‎ ‎ Ⅰ导入新课 ‎ 上一节我们学习了曲线运动，它比直线运动复杂，为研究复杂的运动，就需要把复杂的运动分为简单的运动，本节课我们就来学习一种常用的一种方法——运动的合成和分解。‎ ‎ Ⅱ新课教学 ‎（一）用投影片出示本节课的学习目标 第4页 共4页 ‎ ‎ ‎1、理解什么是合运动，什么是分运动，能在具体实例中找出分运动的合运动和合运动的分运动。‎ ‎2、知道什么是运动的合成，什么是运动的分解。‎ ‎3、理解合运动和分运动的等时性。‎ ‎4、理解合运动是按平行四边形定则由分运动合成的。‎ ‎（二）学习目标完成过程 ‎ 1、合运动和分运动 ‎（1）做课本演示实验：‎ ‎ a在长约80—100cm一端封闭的管中注满清水，水中放一个由红蜡做成的小圆柱体R（要求它能在水中大致匀速上浮），将管的开口端用胶塞塞金。‎ ‎ b，将此管紧贴黑板竖直倒置，在蜡块就沿玻璃管匀速上升，做直线运动，记下它由A移动到B所用的时间。‎ c、然后，将玻璃管重新倒置，在蜡块上升的同时，将玻璃管水平向右匀速移动，观察到它是斜向右上方移动的，经过相同的时间，它由A运动到C。‎ ‎（2）分析：‎ ‎ 红蜡块可看成是同时参与了下面两个运动，在玻璃管中竖直向上的运动（由A到B）和随玻璃管水平向右的运动（由A到D），红蜡块实际发生的运动（由A到C）是这两个运动合成的结果。‎ ‎ （3）用CAI课件重新对比模拟上述运动；‎ ‎ （4）总结得到什么是分运动和合运动。‎ 板：‎ ‎ ①红蜡块实际发生的运动(A C)叫做合运动；‎ 红蜡块沿玻璃管在竖直方向的运动(A B)和随管做的水平方向的运动(A D)，叫做分运动。‎ ‎ ②合运动的（位移、速度）叫做合（位移、速度）；‎ ‎ 分运动的（位移、速度）叫做分（位移、速度）。‎ 在研究雨滴和船的运动时，解决问题的关键是先确定雨滴、小船的合运动。‎ ‎③如何确定一个具体运动的合运动及分运动？‎ a、合运动——对象实际发生的运动；‎ b、合运动在中央，分运动在两边。‎ 请说出下列两个例子中的合运动与分运动(投影)‎ 例1、风中雨点下落v1表示风速，v2表示没风时雨滴下落速度，v表示雨滴合速度。‎ 例2、关于小船渡河（如图）：v静表示船在静水中的运动速度，方向由船头指向确定。 v水 第4页 共4页 ‎ ‎ 表示水的流速，v表示雨滴合速度。‎ ‎　　 ‎ 板：‎ ‎2、合运动与分运动的关系 ‎①等时性：合运动与分运动是同时进行，同时结束。‎ ‎②独立性：一个物体同时参与几个分运动，各分运动独立进行各自产生的效果互不干扰。‎ ‎3、运动的合成和分解：‎ ‎①‎ ‎ ‎ ‎②运动的合成和分解遵循平行四边形法则。‎ ‎（三）例题分析 例1：1、出示分析思考题 ‎ （1）说明红蜡块参与哪两个分运动；‎ ‎ （2）据实验观察知道，分运动和合运动所用的时间有什么关系？‎ ‎ （3）红蜡块的两个分速度应如何求解？‎ ‎ （4）如何分解合速度？‎ ‎ 2、分析解答上述几个问题后，用实物投影仪展示解题过程 解：‎ 竖直方向的分速度 水平方向的分速度 ‎ 合速度: ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎4、同学们看课本的解题过程，并说明是如何求解的。‎ ‎5、例题小结：例1是将演示实验过程定量讨论．给出两个分运动s1、s2及合、分运动的时间t，求合速度v 。‎ ‎　　法一：先求出两个分速度v1=、v2=再利用矢量合成求v 。‎ ‎　　法二：先利用矢量合成求出s，再由v= 求出v 。‎ 例2：飞机飞行给出v合 第4页 共4页 ‎ ‎ 及与某一分速度的角度，来求另外两个分速度。其思路先由平行四边形定则画出几何关系，再利用数学计算解决分速度问题。‎ ‎　　两道例题很简单，但合、分运动关系及解决问题的方法、思路充分体现出来。通过练习使学生们加深了对合、分运动的理解。‎ 练习：设想河水并不流动，汽艇以10㎞/h的速度在垂直于河岸的方向匀速行驶，河宽500m，汽艇驶到对岸需要多长时间？由于河水的流动，汽艇同时被河水冲向下游，沿河运动的速度跟河水流动的速度相同，如果河水流速是3km/h，汽艇驶到对岸需要多长时间？汽艇在对岸何处靠岸？如果河水流速是2km/h或4km/h，上述答案又如何？‎ 关于分运动的性质决定合运动的性质和轨迹：课本以蜡块的运动说明两个直线运动的合运动不一定都是直线运动。为了搞清楚蜡块哪种情况下做直线运动，哪种情况下做曲线运动。这里可以让学生自己探究，得出结论：两个直线的合运动也可以是曲线运动。研究复杂的运动，可以根据不同方向分运动来研究复杂运动情况。‎ ‎　　关于思考与讨论：本节只研究了互成角度的运动，其合成和分解遵从矢量合成规律——平行四边形定则。那么初速度为v0的匀变速直线运动，可以看作同一直线上哪两个分运动的合运动？引导学生对同一直线上的运动合成和分解问题进行讨论，得出该运动也满足矢量合成规律（注意正方向），使我们对矢量合成与分解的规律有了更深的理解。‎ ‎ Ⅲ小结：‎ ‎ 本节课我们主要学习了 ‎ 1：什么是合运动和分运动；‎ ‎ 2：什么是运动的合成和分解；‎ ‎ 3：运动的合成和分解遵循平行四边形法则；‎ ‎ 4：分运动和合运动具有等时性。‎ ‎ Ⅳ作业：‎ ‎ 本章练习二1、2、3、4‎ Ⅴ、板书设计：(略)‎ Ⅵ练习反馈 ‎1、关于运动的合成与分解的说法中，正确的是（   ）‎ A．合运动的位移为分运动的位移的矢量和。‎ B．合运动的速度一定比其中一个分速度大。‎ C．合运动的时间为分运动时间之和。‎ D．合运动的时间与各分运动时间相等。‎ ‎2、下雨时，雨点竖直下落到地面，速度约10m／s。若在地面上放一横截面积为80cm2、高10cm的圆柱形量筒，经30min，筒内接得雨水高2cm．现因风的影响，雨水下落时偏斜30°，求风速及雨滴实际落地时的速度？若用同样的量筒接雨水与无风所用时间相同，则所接雨水高为多少？‎ ‎3、一个小孩坐在匀速行驶的车上，手中拿着小石块，将手伸向窗外后松手，站在地面上的人看到小石块的运动轨迹什么？（可实际观察此过程，然后分析原因）‎ ‎4、一条河宽400m，水流的速度为0.25m／s，船相对静水的速度0.5m／s。‎ ‎　　（1）要想渡河的时间最短，船应向什么方向开出？渡河的最短时间是多少？此时船沿河岸方向漂移多远？‎ ‎　　（2）要使渡河的距离最短，船应向什么方向开出？‎ ‎　　（3）船渡河的时间与水流速度有关吗？‎ 第4页 共4页