2020高中物理第二章第2节匀速圆周运动的向心力和向心加速度2匀速圆周运动的解题技巧学案

2020高中物理第二章第2节匀速圆周运动的向心力和向心加速度2匀速圆周运动的解题技巧学案

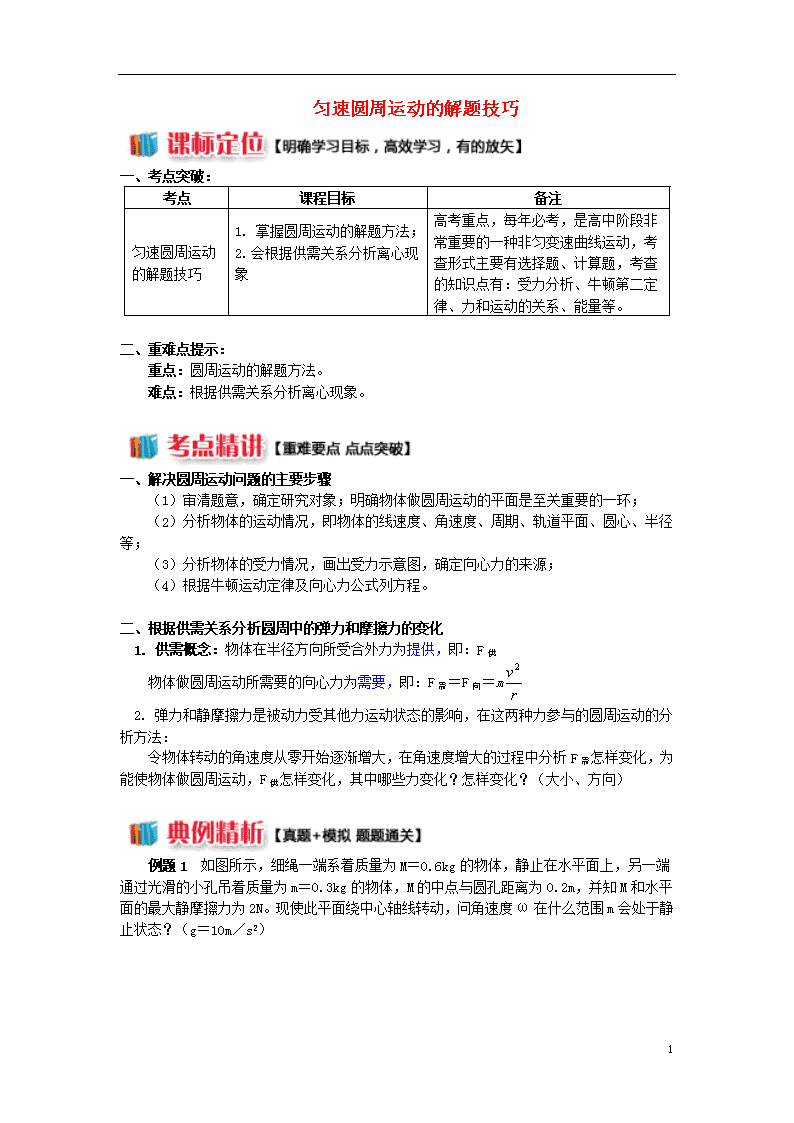
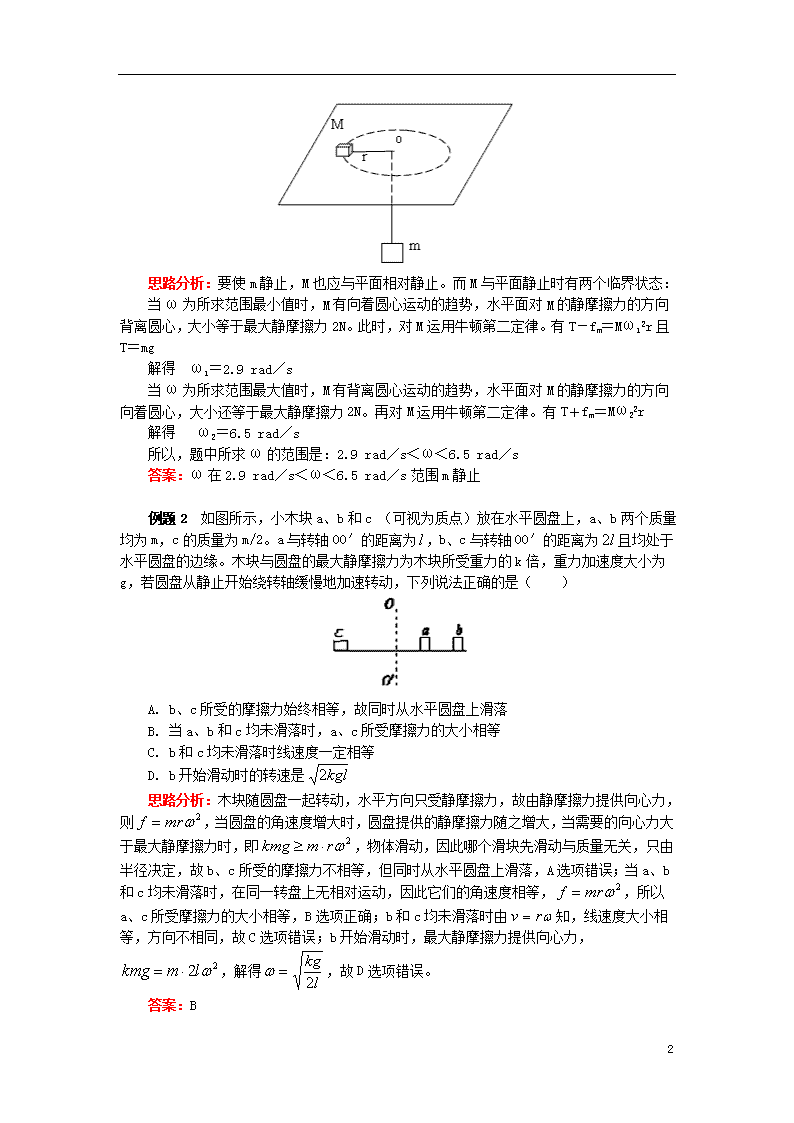
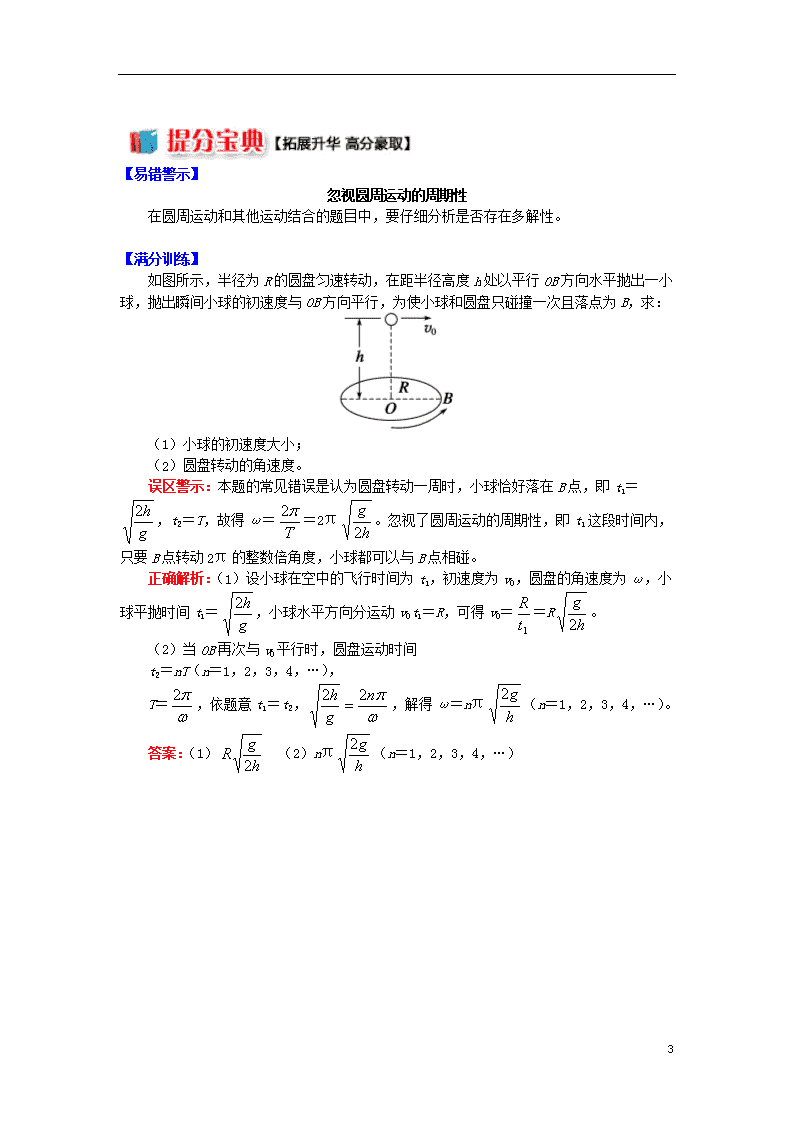
匀速圆周运动的解题技巧 一、考点突破：‎ 考点 课程目标 备注 匀速圆周运动的解题技巧 1. ‎ 掌握圆周运动的解题方法；‎ 2. ‎ 会根据供需关系分析离心现象 高考重点，每年必考，是高中阶段非常重要的一种非匀变速曲线运动，考查形式主要有选择题、计算题，考查的知识点有：受力分析、牛顿第二定律、力和运动的关系、能量等。‎ 二、重难点提示：‎ 重点：圆周运动的解题方法。‎ 难点：根据供需关系分析离心现象。‎ 一、解决圆周运动问题的主要步骤 ‎（1）审清题意，确定研究对象；明确物体做圆周运动的平面是至关重要的一环；‎ ‎（2）分析物体的运动情况，即物体的线速度、角速度、周期、轨道平面、圆心、半径等；‎ ‎（3）分析物体的受力情况，画出受力示意图，确定向心力的来源；‎ ‎（4）根据牛顿运动定律及向心力公式列方程。‎ 二、根据供需关系分析圆周中的弹力和摩擦力的变化 ‎1. 供需概念：物体在半径方向所受合外力为提供，即：F供 物体做圆周运动所需要的向心力为需要，即：F需＝F向＝m ‎2. 弹力和静摩擦力是被动力受其他力运动状态的影响，在这两种力参与的圆周运动的分析方法：‎ 令物体转动的角速度从零开始逐渐增大，在角速度增大的过程中分析F需怎样变化，为能使物体做圆周运动，F供怎样变化，其中哪些力变化？怎样变化？（大小、方向）‎ ‎ ‎ 例题1 如图所示，细绳一端系着质量为M＝‎0.6kg的物体，静止在水平面上，另一端通过光滑的小孔吊着质量为m＝‎0.3kg的物体，M的中点与圆孔距离为‎0.2m，并知M和水平面的最大静摩擦力为2N。现使此平面绕中心轴线转动，问角速度ω在什么范围m会处于静止状态？（g＝‎10m／s2）‎ 3‎ 思路分析：要使m静止，M也应与平面相对静止。而M与平面静止时有两个临界状态：‎ 当ω为所求范围最小值时，M有向着圆心运动的趋势，水平面对M的静摩擦力的方向背离圆心，大小等于最大静摩擦力2N。此时，对M运用牛顿第二定律。有T－fm＝Mω12r且T＝mg 解得 ω1＝2.9 rad／s 当ω为所求范围最大值时，M有背离圆心运动的趋势，水平面对M的静摩擦力的方向向着圆心，大小还等于最大静摩擦力2N。再对M运用牛顿第二定律。有T＋fm＝Mω22r ‎ 解得 　ω2＝6.5 rad／s 所以，题中所求ω的范围是：2.9 rad／s＜ω＜6.5 rad／s 答案：ω在2.9 rad／s＜ω＜6.5 rad／s范围m静止 例题2 如图所示，小木块a、b和c （可视为质点）放在水平圆盘上，a、b两个质量均为m， c的质量为m/2。a与转轴OO′的距离为，b、c与转轴OO′的距离为且均处于水平圆盘的边缘。木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g，若圆盘从静止开始绕转轴缓慢地加速转动，下列说法正确的是（ ）‎ A. b、c所受的摩擦力始终相等，故同时从水平圆盘上滑落 B. 当a、b和c均未滑落时，a、c所受摩擦力的大小相等 C. b和c均未滑落时线速度一定相等 D. b开始滑动时的转速是 思路分析：木块随圆盘一起转动，水平方向只受静摩擦力，故由静摩擦力提供向心力，则，当圆盘的角速度增大时，圆盘提供的静摩擦力随之增大，当需要的向心力大于最大静摩擦力时，即，物体滑动，因此哪个滑块先滑动与质量无关，只由半径决定，故b、c所受的摩擦力不相等，但同时从水平圆盘上滑落，A选项错误；当a、b和c均未滑落时，在同一转盘上无相对运动，因此它们的角速度相等，，所以a、c所受摩擦力的大小相等，B选项正确；b和c均未滑落时由知，线速度大小相等，方向不相同，故C选项错误；b开始滑动时，最大静摩擦力提供向心力，，解得，故D选项错误。‎ 答案：B 3‎ ‎【易错警示】‎ 忽视圆周运动的周期性 在圆周运动和其他运动结合的题目中，要仔细分析是否存在多解性。‎ ‎【满分训练】‎ 如图所示，半径为R的圆盘匀速转动，在距半径高度h处以平行OB方向水平抛出一小球，抛出瞬间小球的初速度与OB方向平行，为使小球和圆盘只碰撞一次且落点为B，求：‎ ‎（1）小球的初速度大小；‎ ‎（2）圆盘转动的角速度。‎ 误区警示：本题的常见错误是认为圆盘转动一周时，小球恰好落在B点，即t1＝，t2＝T，故得ω＝＝2π。忽视了圆周运动的周期性，即t1这段时间内，只要B点转动2π的整数倍角度，小球都可以与B点相碰。‎ 正确解析：（1）设小球在空中的飞行时间为t1，初速度为v0，圆盘的角速度为ω，小球平抛时间t1＝，小球水平方向分运动v0t1＝R，可得v0＝＝R。‎ ‎（2）当OB再次与v0平行时，圆盘运动时间 t2＝nT（n＝1，2，3，4，…），‎ T＝，依题意t1＝t2，，解得ω＝nπ（n＝1，2，3，4，…）。‎ 答案：（1）　（2）nπ（n＝1，2，3，4，…）‎ 3‎