人教版必修一3.5《力的分解》WORD教案9

人教版必修一3.5《力的分解》WORD教案9

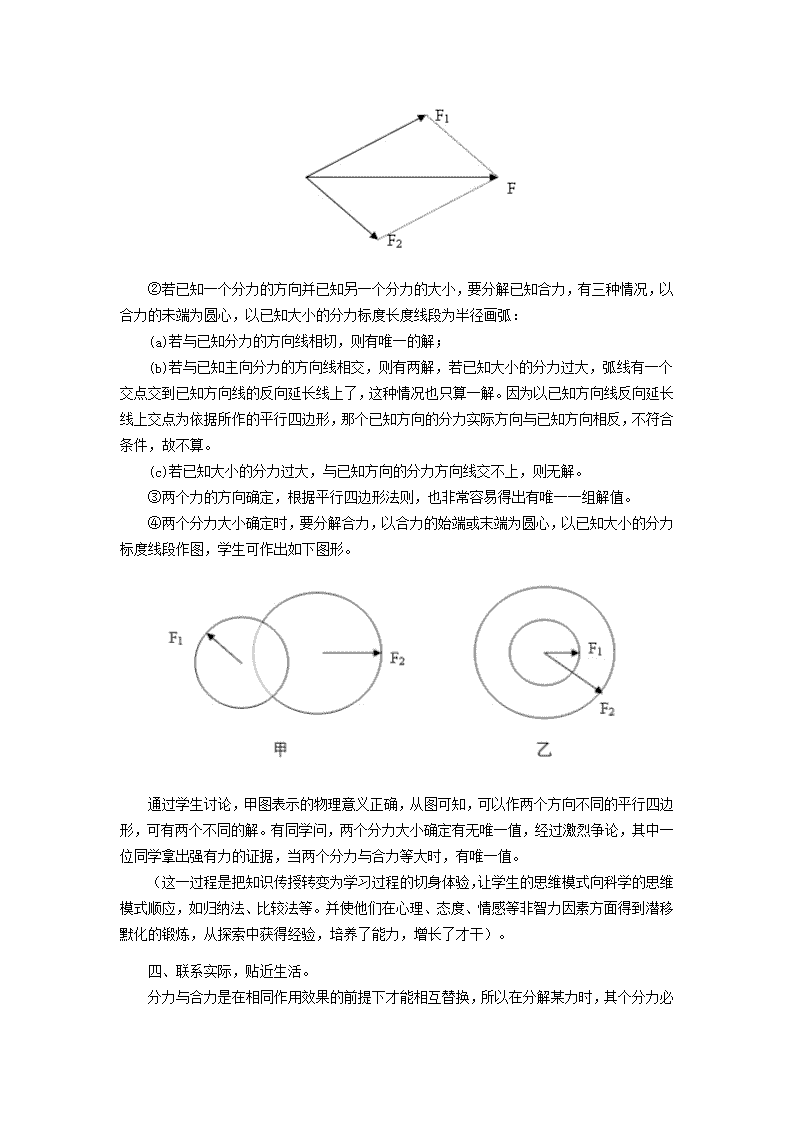
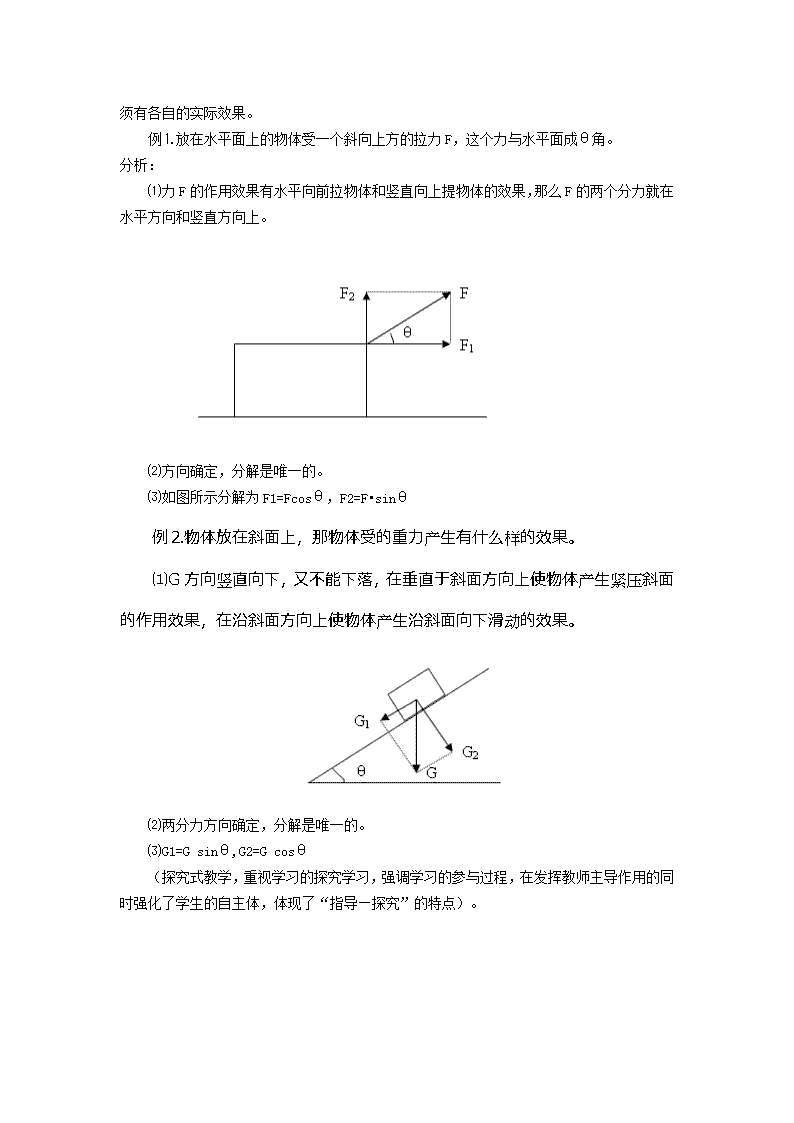
‎　　第三章 相互作用 第八课时 ‎3.5力的分解 教学目标 　　⒈理解力的分解和分力的概念。 　　⒉理解力的分解是力的合成的逆运算，会用作图法求分力，会用直角三角形的知识计算分力。 　　⒊培养学生分析问题，解决问题的能力。 　　⒋力的合成和分解符合对立统一规律。‎ ‎　　一、创设情境，提出课题。 　　在已知分力求合力时，可按平行四边形法则，唯一地求出平行四边形对角线对应的合力，而在已知某力，如何将它分解为两个分力呢？ 　　（运用已掌握的知识作为新知识的生长点，引入要研究新问题，引起思维的，有利于激发学生解决问题的动机）。‎ ‎　　二、启发分析，寻找相关量。 　　⑴什么是分力？什么是力的分解。 　　⑵为什么说力的合成是力的分解的逆运算。 　　学生：某一个力F，可用F1和F2来代替，那这两个力叫F的分力。求一个已知力的分力叫力的分解。 　　力的分解是力的合成的逆运算，当然应该遵循平行四边形法则，按平行四边形法则却可以有无数组解，如何确定一组解呢？力的矢量，如何找到突破口呢？ 　　（老师适当点拔，尽可能让学生进行思维的发散性思考）‎ ‎　　三、师生互动，引导探究，寻找规律。 　　（这是一个规律探究过程，可以让学生自主假设，展开讨论，探究规律，深化思维，教师可作适当引导。体现了“以学生发展为本”的理念）。 　　学生提出假设： 　　①一个分力的大小和方向确定。 　　②一个分力的方向并且另一个分力的大小确定。 　　③两个力的方向确定。 　　④两个力的大小确定。 　　学生探究规律： 　　① 已知一个分力的大小和方向，根据平行四边形法则，合力只有一组解。 ‎　　②若已知一个分力的方向并已知另一个分力的大小，要分解已知合力，有三种情况，以合力的未端为圆心，以已知大小的分力标度长度线段为半径画弧： 　　(a)若与已知分力的方向线相切，则有唯一的解； 　　(b)若与已知主向分力的方向线相交，则有两解，若已知大小的分力过大，弧线有一个交点交到已知方向线的反向延长线上了，这种情况也只算一解。因为以已知方向线反向延长线上交点为依据所作的平行四边形，那个已知方向的分力实际方向与已知方向相反，不符合条件，故不算。 　　(c)若已知大小的分力过大，与已知方向的分力方向线交不上，则无解。 　　③两个力的方向确定，根据平行四边形法则，也非常容易得出有唯一一组解值。 　　④两个分力大小确定时，要分解合力，以合力的始端或末端为圆心，以已知大小的分力标度线段作图，学生可作出如下图形。‎ ‎　　通过学生讨论，甲图表示的物理意义正确，从图可知，可以作两个方向不同的平行四边形，可有两个不同的解。有同学问，两个分力大小确定有无唯一值，经过激烈争论，其中一位同学拿出强有力的证据，当两个分力与合力等大时，有唯一值。 　　（这一过程是把知识传授转变为学习过程的切身体验，让学生的思维模式向科学的思维模式顺应，如归纳法、比较法等。并使他们在心理、态度、情感等非智力因素方面得到潜移默化的锻炼，从探索中获得经验，培养了能力，增长了才干）。‎ ‎　　四、联系实际，贴近生活。 　　分力与合力是在相同作用效果的前提下才能相互替换，所以在分解某力时，其个分力必 须有各自的实际效果。 　　例⒈放在水平面上的物体受一个斜向上方的拉力F，这个力与水平面成θ角。 分析： 　　⑴力F的作用效果有水平向前拉物体和竖直向上提物体的效果，那么F的两个分力就在水平方向和竖直方向上。‎ ‎    ‎ ‎　　⑵方向确定，分解是唯一的。 　　⑶如图所示分解为F1=Fcosθ，F2=F•sinθ ‎　　例⒉物体放在斜面上，那物体受的重力产生有什么样的效果。 　　⑴G方向竖直向下，又不能下落，在垂直于斜面方向上使物体产生紧压斜面的作用效果，在沿斜面方向上使物体产生沿斜面向下滑动的效果。 ‎⑵两分力方向确定，分解是唯一的。 　　⑶G1=G sinθ,G2=G cosθ 　　（探究式教学，重视学习的探究学习，强调学习的参与过程，在发挥教师主导作用的同时强化了学生的自主体，体现了“指导—探究”的特点）。‎