2020高中物理第十九章原子核水平测试卷含解析 人教版选修3-5

2020高中物理第十九章原子核水平测试卷含解析 人教版选修3-5

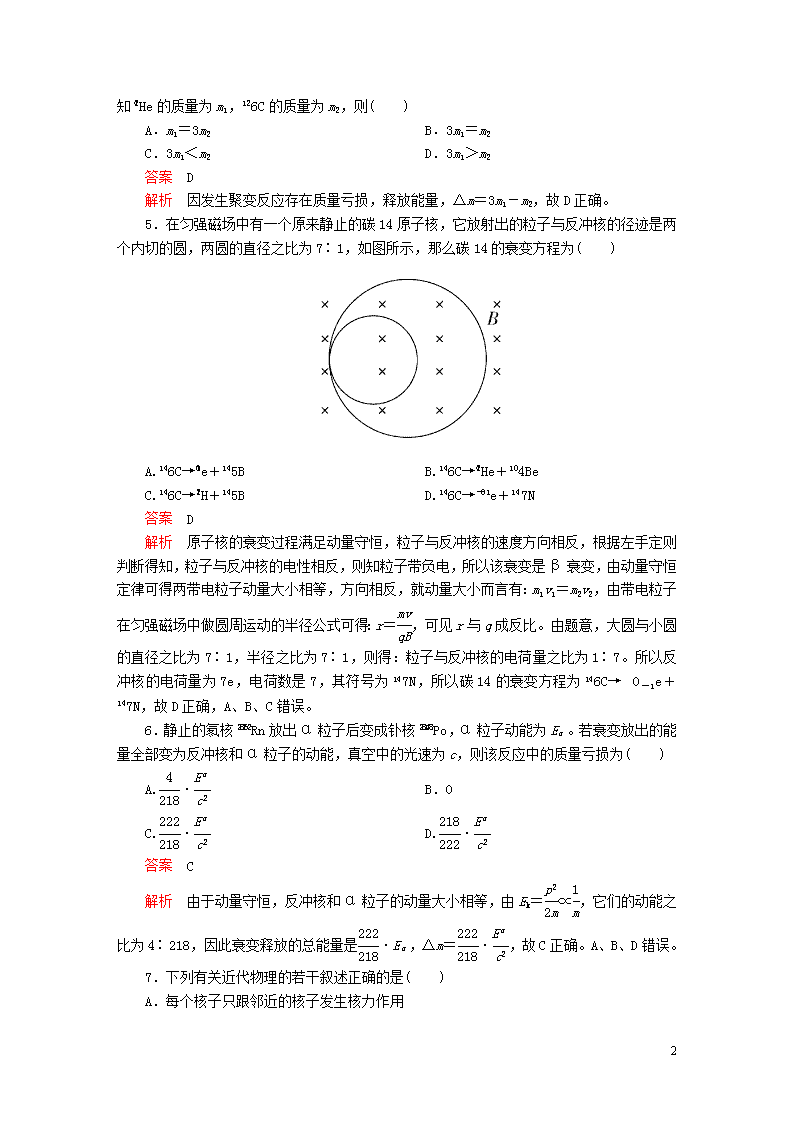
第十九章　水平测试卷 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分100分，考试时间90分钟。‎ 第Ⅰ卷(选择题，共40分)‎ 一、选择题(本题共10小题，每小题4分，共40分。在每小题给出的四个选项中，第1～6题只有一项符合题目要求，第7～10题有多项符合题目要求。全部选对的得4分，选对但不全的得2分，有选错的得0分)‎ ‎1．下列说法中正确的是(　　)‎ A.U的半衰期约为7亿年，随着地球环境的不断变化，其半衰期可能变短 B．某原子核经过一次α衰变和两次β衰变后，核内中子数减少4‎ C．10个放射性元素的原子核经过一个半衰期后，一定有5个原子核发生衰变 D．γ粒子的电离能力比α粒子的大 答案　B 解析　半衰期的长短是由原子核内部本身的因素决定的，与原子所处的物理、化学状态无关，故A错误；某原子核经过一次α衰变电荷数减小2，质量数减小4，再经过两次β衰变后，质量数不变，电荷数要增加2，所以整个过程质量数减小4，电荷数不变，所以核内中子数减少4个。故B正确。半衰期具有统计规律，对大量的原子核适用。故C错误。三种射线中γ射线的穿透能力最强，α射线的电离能力最强，故D错误。‎ ‎2．在正负电子对撞机中，一个电子和一个正电子对撞发生湮灭而转化为一对光子。设正、负电子的质量在对撞前均为m，对撞前的动能均为E，光在真空中的传播速度为c，普朗克常量为h，则对撞后转化成光子的波长等于(　　)‎ A. B. C. D. 答案　C 解析　一个光子的能量为mc2＋E，h＝mc2＋E，所以λ＝，C正确。‎ ‎3．将半衰期为5天的铋64 g分成四份分别投入(1)开口容器中；(2)100 atm的密封容器中；(3)100 ℃的沸水中，第四份则与别的元素形成化合物，经10天后，四种情况剩下的质量分别为m1、m2、m3、m4，则(　　)‎ A．m1＝m2＝m3＝m4＝4 g B．m1＝m2＝m3＝4 g, m4<4 g C．m1>m2>m3>m4，m1＝4 g D．m1＝4 g，其余无法知道 答案　A 解析　放射性元素的半衰期是一定的，与放射性元素所在的物理环境和化学环境无关，所以A正确。‎ ‎4．现在太阳向外辐射的能量是由于太阳内部氢核聚变产生的。科学家预测：大约在40亿年以后，太阳内部还将会启动另一种核反应，其核反应方程为：He＋He＋He→6C，已知He的质量为m1，6C的质量为m2，则(　　)‎ 6‎ A．m1＝3m2 B．3m1＝m2‎ C．3m1＜m2 D．3m1＞m2‎ 答案　D 解析　因发生聚变反应存在质量亏损，释放能量，Δm＝3m1－m2，故D正确。‎ ‎5．在匀强磁场中有一个原来静止的碳14原子核，它放射出的粒子与反冲核的径迹是两个内切的圆，两圆的直径之比为7∶1，如图所示，那么碳14的衰变方程为(　　)‎ A.6C→e＋5B B.6C→He＋4Be C.6C→H＋5B D.6C→e＋7N 答案　D 解析　原子核的衰变过程满足动量守恒，粒子与反冲核的速度方向相反，根据左手定则判断得知，粒子与反冲核的电性相反，则知粒子带负电，所以该衰变是β衰变，由动量守恒定律可得两带电粒子动量大小相等，方向相反，就动量大小而言有：m1v1＝m2v2，由带电粒子在匀强磁场中做圆周运动的半径公式可得：r＝，可见r与q成反比。由题意，大圆与小圆的直径之比为7∶1，半径之比为7∶1，则得：粒子与反冲核的电荷量之比为1∶7。所以反冲核的电荷量为7e，电荷数是7，其符号为7N，所以碳14的衰变方程为6C→　0－1e＋7N，故D正确，A、B、C错误。‎ ‎6．静止的氡核Rn放出α粒子后变成钋核Po，α粒子动能为Eα。若衰变放出的能量全部变为反冲核和α粒子的动能，真空中的光速为c，则该反应中的质量亏损为(　　)‎ A.· B．0‎ C.· D.· 答案　C 解析　由于动量守恒，反冲核和α粒子的动量大小相等，由Ek＝∝，它们的动能之比为4∶218，因此衰变释放的总能量是·Eα，Δm＝·，故C正确。A、B、D错误。‎ ‎7．下列有关近代物理的若干叙述正确的是(　　)‎ A．每个核子只跟邻近的核子发生核力作用 B．四个核子聚变为一个氦核的过程释放的核能等于氦核质量与c2的乘积 C．太阳内部发生的核反应是热核反应 6‎ D．关于原子核内部的信息，最早来自天然放射现象 答案　ACD 解析　核力为短程力，每个核子只能跟邻近的核子产生核力的作用，故A正确；根据爱因斯坦的质能方程，四个核子聚变为一个氦核的过程释放的核能等于亏损的质量与c2的乘积，不是等于氦核质量与c2的乘积，故B错误；太阳内部发生的是热核反应，故C正确；关于原子核内部的信息，最早来自天然放射现象，故D正确。‎ ‎8．关于放射性同位素的应用，下列说法正确的是(　　)‎ A．放射线改变了布料的性质使其不再因摩擦而生电，因此达到消除有害静电的目的 B．用放射线照射作物种子能使其DNA发生变异，其结果一定是成为更优秀的品种 C．用γ射线治疗肿瘤时一定要严格控制剂量，以免对人体正常组织造成太大的危害 D．γ射线对人体细胞伤害太大，不能直接用来进行人体透视 答案　CD 解析　利用放射线消除有害静电是利用α射线的电离性，使空气分子电离成导体，将静电中和，故A错误；DNA变异并不一定都是有益的，有时也会向有害的一面变异，故B错误；γ射线对人体细胞伤害太大，在用于治疗肿瘤时要严格控制剂量，故C正确；γ射线对人体细胞伤害太大，不能直接用来进行人体透视，故D正确。‎ ‎9．钍核Th经过6次α衰变和4次β衰变后变成铅核，则(　　)‎ A．铅核的符号为Pb，它比Th少8个质子 B．铅核的符号为Pb，它比Th少16个中子 C．铅核的符号为Pb，它比Th少16个中子 D．铅核的符号为Pb，它比Th少12个中子 答案　AC 解析　设铅的质量数为M，核电荷数为Z，则由质量数守恒可得：M＝232－6×4＝208。由电荷数守恒可得：Z＝90－6×2＋4×1＝82。则铅核的中子数＝208－82＝126，钍核的中子数＝232－90＝142。所以铅核的中子数比钍核中子数少16个，铅核的质子数比钍核质子数少8个。A、C正确，B、D错误。‎ ‎10．中子和质子结合成氘核时，质量亏损为Δm，相应的能量ΔE＝Δmc2＝2.2 MeV是氘核的结合能。下列说法正确的是(　　)‎ A．用能量小于2.2 MeV的光子照射静止氘核时，氘核不能分解为一个质子和一个中子 B．用能量等于2.2 MeV的光子照射静止氘核时，氘核可能分解为一个质子和一个中子，它们的动能之和为零 C．用能量大于2.2 MeV的光子照射静止氘核时，氘核可能分解为一个质子和一个中子，它们的动能之和为零 D．用能量大于2.2 MeV的光子照射静止氘核时，氘核可能分解为一个质子和一个中子，它们的动能之和不为零 答案　AD 解析　氘核分解为一个质子和一个中子时，所需吸收的能量不能小于其结合能2.2‎ 6‎ ‎ MeV，故A正确；光子照射氘核时，光子和氘核组成的系统总动量不为零，由动量守恒定律得，光子被氘核吸收后，分解成的质子和中子的总动量不为零，故总动能也不为零，所以把氘核分解为质子和中子所需的能量应大于2.2 MeV，故D正确，B、C错误。‎ 第Ⅱ卷(非选择题，共60分)‎ 二、填空题(本题共3小题，共15分)‎ ‎11．(6分)现有三个核反应(衰变)方程：‎ A.Na→Mg＋　0－1e B.U＋n→Ba＋Kr＋3n C.H＋H→He＋n 则________是β衰变；________是裂变；________是聚变。(填正确答案标号)‎ 答案　A　B　C 解析　衰变是指原子核放出α粒子和β粒子后，变成新的原子核的变化，A是β衰变；裂变是重核分裂成质量较小的核，B是裂变；聚变是轻核结合成质量较大的核，C是聚变。‎ ‎12．(3分)可研制核武器的钚239(Pu)可由铀239(U)经过x次β衰变而产生，则x等于________。‎ 答案　2‎ 解析　由衰变方程92Pu→U＋2e，可知x＝2。‎ ‎13．(6分)“反粒子”与其对应的正粒子具有相同的质量和电荷量，但电荷的符号相反，例如正电子就是电子的“反粒子”。据此，若有反质子存在，它的质量数应为________，元电荷的电荷量是1.60×10－19 C，则反质子的电荷量为________。‎ 答案　1　－1.60×10－19 C 解析　质子的质量数为1，电荷量为1.60×10－19 C，所以反质子的质量数为1，电荷量大小也为1.60×10－19 C，电性相反。‎ 三、计算题(本题共4小题，共45分。要有必要的文字说明和解题步骤，有数值计算的要注明单位)‎ ‎14．(11分)放射性同位素6C被考古学家称为“碳钟”，它可用来断定古生物的年代，此项研究获得1960年诺贝尔化学奖。‎ ‎(1)宇宙射线中高能量的中子碰到空气中的氮原子核后，会形成6C，6C很不稳定，易发生衰变，其半衰期为5730年，衰变时会放出β射线，试写出有关核反应(衰变)方程；‎ ‎(2)若测得一古生物遗骸中6C含量只有活体中的12.5%，则此遗骸的年代约有多少年？‎ 答案　(1)见解析　(2)17190年 解析　(1)7N＋n→6C＋H，6C→7N＋e。‎ ‎(2)依题意n＝＝0.125，‎ 解得n＝3，则t＝5730×3年＝17190年。‎ ‎15．(11分)一个质量为M、电荷量为Q的原子核发生 α衰变，α粒子的运动速度为v，假设质子的质量为m，电荷量为q，衰变过程中放出的能量全部转化为动能，则衰变过程的质量亏损为多少？‎ 答案　Δm＝ 解析　若质子的质量为m，电荷量为q，则α粒子的质量为4m，电荷量为2q 6‎ ‎，显然质量为M的原子核发生α衰变后新核的质量为M－4m，电荷量为Q－2q。‎ 设新核的速度为v′。‎ 依据动量守恒定律有：‎ ‎0＝(M－4m)v′－4mv，‎ 解得v′＝。‎ 依据能量守恒可得 ×4mv2＋(M－4m)v′2＝Δmc2，‎ 解得Δm＝。‎ ‎16. (11分)如图所示，有界的匀强磁场磁感应强度为B＝0.05 T，磁场方向垂直于纸面向里，MN是磁场的左边界。在磁场A处放一个放射源，内装Ra，放出某种射线后衰变成Rn。‎ ‎(1)写出上述衰变方程；‎ ‎(2)若A处距磁场边界MN的距离OA＝1.0 m时，放在MN左侧边缘的粒子接收器接收到垂直于边界MN方向射出的质量较小的粒子，此时接收器距过OA的直线1.0 m。已知Rn、He质量分别为222 u、4 u，求一个静止Ra核衰变过程中释放的核能有多少？(取1 u＝1.66×10－27 kg，e＝1.60×10－19 C)‎ 答案　(1)Ra→Rn＋He　(2)1.96×10－14 J 解析　(1)Ra比Rn电荷数多2，质量数多4，则该衰变为α衰变，方程为Ra→Rn＋He；‎ ‎(2)衰变过程中释放的α粒子在磁场中做匀速圆周运动，轨道半径R＝1.0 m，‎ 由洛伦兹力提供向心力，可得2evB＝，‎ 衰变过程中系统动量守恒，有0＝222 u×v′－4 u×v，‎ 所以，释放的核能E＝×222 u×v′2＋×4 u×v2，‎ 代入数据解得E≈1.96×10－14 J。‎ ‎17．(12分)如图甲所示，静止在匀强磁场中的Li核俘获一个速度为v0＝7.7×104 m/s的中子而发生核反应，即Li＋n→H＋He，若已知He的速度v2＝2.0×104 m/s，其方向与反应前中子速度方向相同，试求：‎ 6‎ ‎(1)H的速度大小和方向；‎ ‎(2)在图乙中，已画出并标明两粒子的运动轨迹，请计算出轨道半径之比；‎ ‎(3)当He旋转三周时，粒子H旋转几周？‎ 答案　(1)大小为1.0×103 m/s，方向与v0相反 ‎(2)3∶40　(3)2周 解析　(1)反应前后动量守恒：m0v0＝m1v1＋m2v2(v1为氚核速度，m0、m1、m2分别代表中子、氚核、氦核质量)‎ 代入数值可解得：v1＝－1.0×103 m/s，方向与v0相反。‎ ‎(2)H和He在磁场中均受洛伦兹力，做匀速圆周运动的轨道半径之比r1∶r2＝∶＝3∶40。‎ ‎(3)H和He做匀速圆周运动的周期之比 T1∶T2＝∶＝3∶2，‎ 所以它们的旋转周数之比：n1∶n2＝T2∶T1＝2∶3，即He旋转三周，H旋转2周。‎ 6‎