新教材高中物理第2章抛体运动知识网络建构与学科素养提升学案鲁科版必修第二册

新教材高中物理第2章抛体运动知识网络建构与学科素养提升学案鲁科版必修第二册

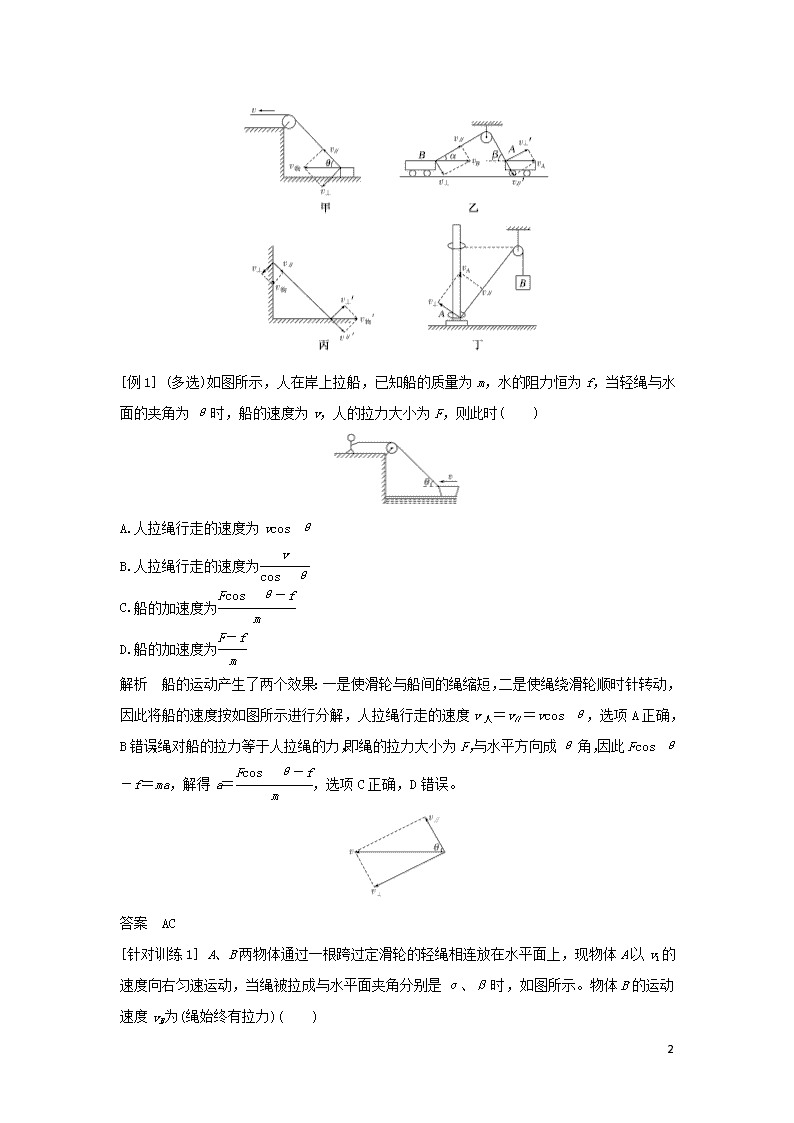
知识网络建构与学科素养提升 一、“绳(杆)关联物体”的速度分解问题 ‎1.模型特点 沿绳(杆)方向的速度分量大小相等。‎ ‎2.思路与方法 合速度→绳(杆)拉物体的实际运动速度v 分速度→ 方法：v1与v2的合成遵循平行四边形定则。‎ ‎3.解题的原则 把物体的实际速度分解为垂直于绳(杆)和平行于绳(杆)两个分量，根据沿绳(杆)方向的分速度大小相等求解。常见的模型如图所示。‎ 5‎ ‎[例1] (多选)如图所示，人在岸上拉船，已知船的质量为m，水的阻力恒为f，当轻绳与水面的夹角为θ时，船的速度为v，人的拉力大小为F，则此时(　　)‎ A.人拉绳行走的速度为vcos θ B.人拉绳行走的速度为 C.船的加速度为 D.船的加速度为 解析　船的运动产生了两个效果：一是使滑轮与船间的绳缩短，二是使绳绕滑轮顺时针转动，因此将船的速度按如图所示进行分解，人拉绳行走的速度v人＝v∥＝vcos θ，选项A正确，B错误；绳对船的拉力等于人拉绳的力，即绳的拉力大小为F，与水平方向成θ角，因此Fcos θ－f＝ma，解得a＝，选项C正确，D错误。‎ 答案　AC ‎[针对训练1] A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体A以v1的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图所示。物体B的运动速度vB为(绳始终有拉力)(　　)‎ 5‎ A. B. C. D. 解析　设物体B的运动速度为vB，此速度为物体B合运动的速度。根据它的实际运动效果，两分运动分别为沿绳收缩方向的分运动，设其速度为v绳B；垂直绳方向的圆周运动，速度分解如图甲所示，则有vB＝　①；物体A的合运动对应的速度为v1，它也产生两个分运动效果，分别是沿绳伸长方向的分运动，设其速度为v绳A；垂直绳方向的圆周运动，它的速度分解如图乙所示，则v绳A＝v1cos α　②；由于对应同一根绳，其长度不变，故v绳B＝v绳A　③；根据①②③解得vB＝，选项D正确。‎ 答案　D 二、平抛运动的临界和极值问题 ‎1.常见的“三种”临界特征 ‎(1)有些题目中有“刚好”“恰好”“正好”等字眼，明显表明题述的过程中存在着临界点。‎ ‎(2)若题目中有“取值范围”“多长时间”“多大距离”等词语，表明题述的过程中存在着“起止点”，而这些起止点往往就是临界点。‎ ‎(3)若题目中有“最大”“最小”“至多”“至少”等字眼，表明题述的过程中存在着极值，这个极值点往往是临界点。‎ ‎2.求解平抛运动中的临界问题的三个关键点 ‎(1)确定运动性质——匀变速曲线运动。‎ ‎(2)确定临界状态。确定临界状态一般用极限法分析，即把平抛运动的初速度增大或减小，使临界状态呈现出来。‎ ‎(3)确定临界状态的运动轨迹，并画出轨迹示意图。画示意图可以使抽象的物理情景变得直观，更可以使有些隐藏于问题深处的条件暴露出来。 ‎ 5‎ ‎[例2] 如图所示，水平屋顶高H＝5 m，墙高h＝3.2 m，墙到房子的距离L＝3 m，墙外马路宽x＝10 m，小球从房顶水平飞出，落在墙外的马路上，不计空气阻力，g＝10 m/s2。求：‎ ‎(1)小球离开屋顶时的速度v0的大小范围；‎ ‎(2)小球落在马路上的最小速度。‎ 解析　(1)设小球恰好落到马路的右侧边缘时，水平初速度为v01，则L＋x＝v01t1‎ 竖直位移H＝gt 联立解得v01＝(L＋x) ＝13 m/s 设小球恰好越过围墙的边缘时，水平初速度为v02，则 水平位移L＝v02t2‎ 竖直位移H－h＝gt 联立解得v02＝5 m/s 所以小球抛出时的速度大小范围为5 m/s≤v0≤13 m/s。‎ ‎(2)小球落在马路上，下落高度一定，落地时的竖直分速度一定，当小球恰好越过围墙的边缘落在马路上时，落地速度最小。‎ 竖直方向v＝2gH 又有vmin＝ 解得vmin＝5 m/s。‎ 答案　(1)5 m/s≤v0≤13 m/s　(2)5 m/s ‎[针对训练2] 一带有乒乓球发射机的乒乓球台如图所示。水平台面的长和宽分别为L1和L2，中间球网高度为h。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h。不计空气的作用，重力加速度大小为g。若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是(　　)‎ 5‎ A.＜v＜L1 B.＜v＜ C.＜v＜ D.＜v＜ 解析　设以速率v1发射乒乓球，经过时间t1刚好落到球网正中间。‎ 则竖直方向上有3h－h＝gt，①‎ 水平方向上有＝v1t1。②‎ 由①②两式可得v1＝。‎ 设以速率v2发射乒乓球，经过时间t2刚好落到球网右侧台面的两角处，‎ 在竖直方向有3h＝gt，③‎ 在水平方向有＝v2t2。④‎ 由③④两式可得v2＝。‎ 则v的最大取值范围为v1＜v＜v2，故选项D正确。‎ 答案　D 5‎