高中物理第2章研究圆周运动2_3圆周运动的案例分析教学案
圆周运动的案例分析
[学习目标] 1.通过向心力的实例分析,体会匀速圆周运动在生活、生产中的应用.2.能应用
向心力和向心加速度公式分析过山车问题和火车转弯问题.3.熟练掌握应用牛顿第二定律和
向心力知识分析两类竖直面内圆周运动模型的步骤和方法.
一、过山车问题
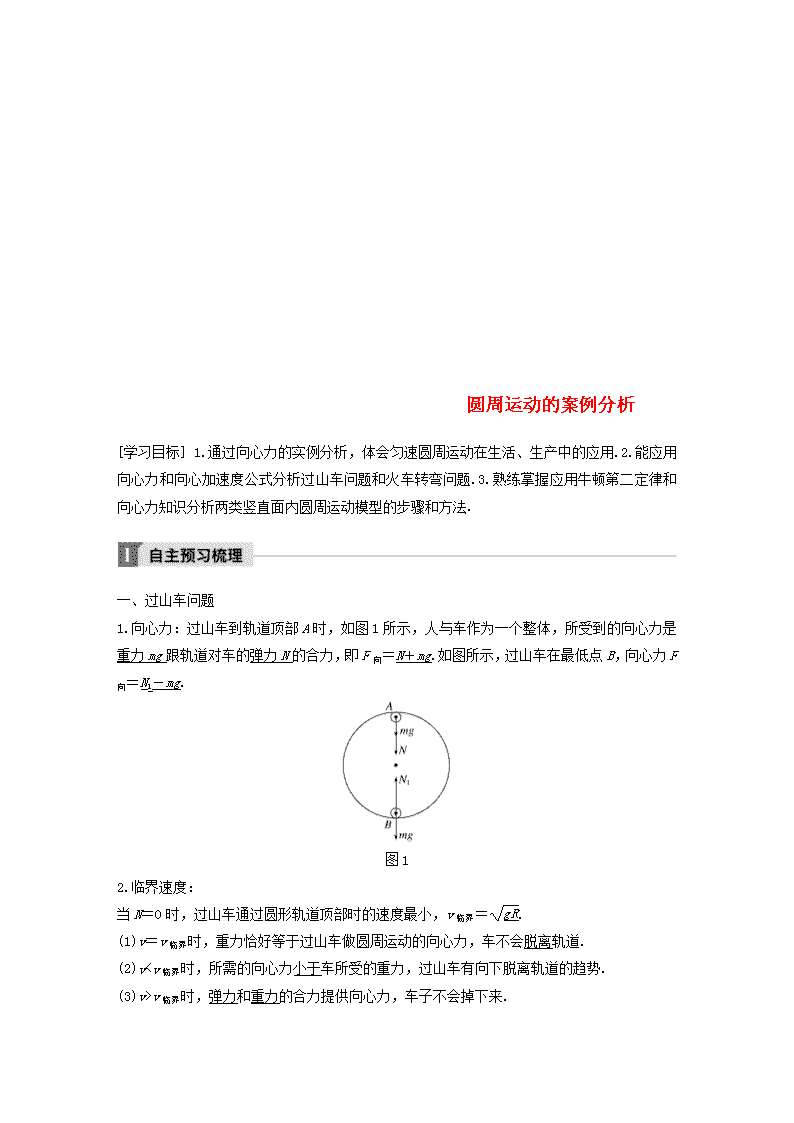
1.向心力:过山车到轨道顶部 A 时,如图 1 所示,人与车作为一个整体,所受到的向心力是
重力 mg 跟轨道对车的弹力 N 的合力,即 F 向=N+mg.如图所示,过山车在最低点 B,向心力 F
向=N1-mg.
图 1
2.临界速度:
当 N=0 时,过山车通过圆形轨道顶部时的速度最小,v 临界= gR.
(1)v=v 临界时,重力恰好等于过山车做圆周运动的向心力,车不会脱离轨道.
(2)v
v 临界时,弹力和重力的合力提供向心力,车子不会掉下来.
二、运动物体的转弯问题
1.自行车在水平路面转弯,地面对车的作用力与重力的合力提供转弯所需的向心力.
2.汽车在水平路面转弯,所受静摩擦力提供转弯所需的向心力.
3.火车转弯时外轨高于内轨,如图 2 所示,向心力由支持力和重力的合力提供.
图 2
[即学即用]
1.判断下列说法的正误.
(1)汽车在水平路面上正常转弯时所需要的向心力是滑动摩擦力提供的.(×)
(2)火车转弯时,内、外轨道一样高.(×)
(3)若铁路弯道的内外轨一样高,火车通过弯道时向心力的来源是外轨的水平弹力,所以外轨
容易磨损.(√)
(4)汽车行驶至凸形桥顶部时,对桥面的压力等于车重.(×)
(5)汽车行驶至凹形桥底部时,对桥面的压力大于车重.(√)
(6)绕地球做匀速圆周运动的航天器中的宇航员处于完全失重状态,故不再具有重力.(×)
2.飞机由俯冲转为拉起的一段轨迹可看成一段圆弧,如图 3 所示,飞机做俯冲拉起运动时,
在最低点附近做半径为 r=180 m 的圆周运动,如果飞行员质量 m=70 kg,飞机经过最低点 P
时的速度 v=360 km/h,则这时飞行员对座椅的压力是________.(g 取 10 m/s2)
图 3
答案 4 589 N
解析 飞机经过最低点时,v=360 km/h=100 m/s.
对飞行员进行受力分析,飞行员在竖直面内共受到重力 G 和座椅的支持力 N 两个力的作用,
根据牛顿第二定律得 N-mg=mv2
r
,所以 N=mg+mv2
r
=70×10 N+70×1002
180
N≈4 589 N,由牛
顿第三定律得,飞行员对座椅的压力为 4 589 N.
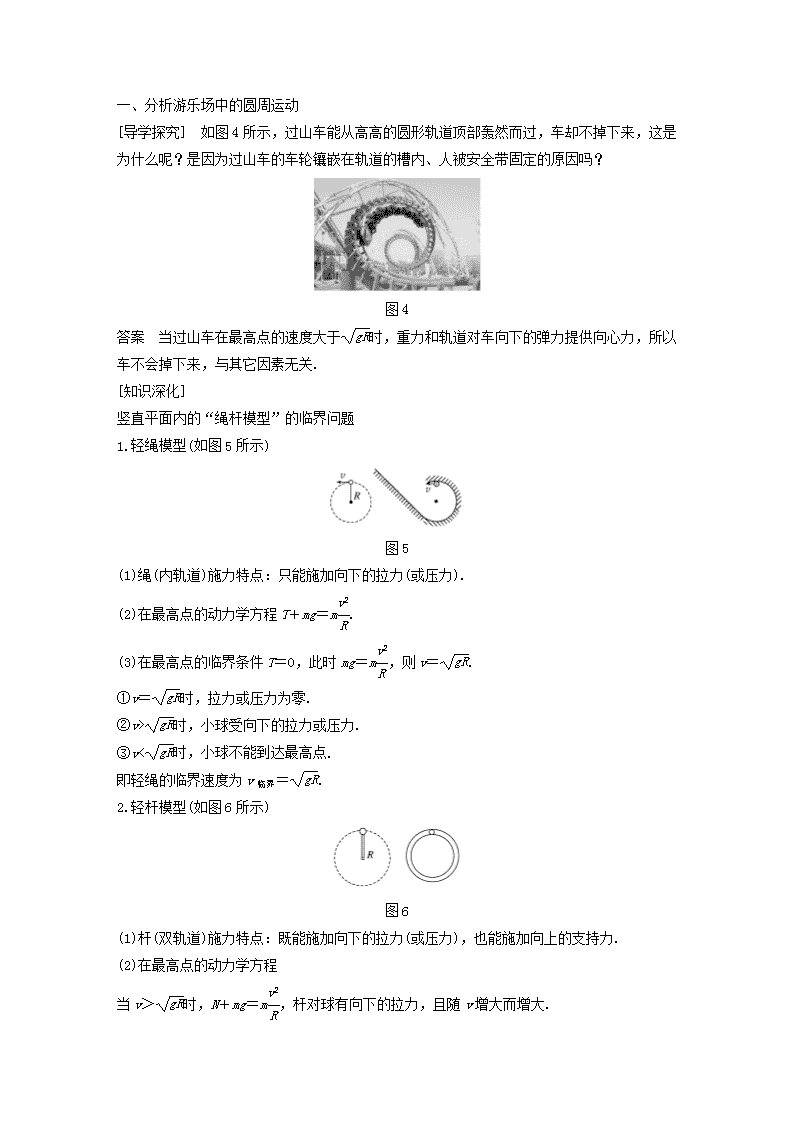
一、分析游乐场中的圆周运动
[导学探究] 如图 4 所示,过山车能从高高的圆形轨道顶部轰然而过,车却不掉下来,这是
为什么呢?是因为过山车的车轮镶嵌在轨道的槽内、人被安全带固定的原因吗?
图 4
答案 当过山车在最高点的速度大于 gR时,重力和轨道对车向下的弹力提供向心力,所以
车不会掉下来,与其它因素无关.
[知识深化]
竖直平面内的“绳杆模型”的临界问题
1.轻绳模型(如图 5 所示)
图 5
(1)绳(内轨道)施力特点:只能施加向下的拉力(或压力).
(2)在最高点的动力学方程 T+mg=mv2
R
.
(3)在最高点的临界条件 T=0,此时 mg=mv2
R
,则 v= gR.
①v= gR时,拉力或压力为零.
②v> gR时,小球受向下的拉力或压力.
③v< gR时,小球不能到达最高点.
即轻绳的临界速度为 v 临界= gR.
2.轻杆模型(如图 6 所示)
图 6
(1)杆(双轨道)施力特点:既能施加向下的拉力(或压力),也能施加向上的支持力.
(2)在最高点的动力学方程
当 v> gR时,N+mg=mv2
R
,杆对球有向下的拉力,且随 v 增大而增大.
当 v= gR时,mg=mv2
R
,杆对球无作用力.
当 v< gR时,mg-N=mv2
R
,杆对球有向上的支持力.
当 v=0 时,mg=N,球恰好能到达最高点.
(3)杆类的临界速度为 v 临界=0.
例 1 公园里的过山车驶过最高点时,乘客在座椅里面头朝下.若轨道半径为 R,人的质量为
m.
(1)若过山车安全通过最高点,必须至少具备多大的速度?
(2)若过最高点时人对座椅的压力为 2mg,则过山车在最高点时的速度是多大?
答案 (1) gR (2) 3gR
解析 (1)人恰好通过最高点时,座椅对人的压力为零.人只有重力提供向心力,根据牛顿第
二定律.mg=mv 2
1
R
得:v1= gR,即为安全通过最高点的最小速度
(2)若人对座椅的压力 N′=2mg,在最高点人受座椅向下的弹力和重力,两个力的合力提供
向心力,有:
mg+N=mv 2
2
R
得:v2= 3gR
例 2 如图 7 所示,质量为 m 的小球固定在长为 l 的细轻杆的一端,绕轻杆的另一端 O 在竖
直平面内做圆周运动.球转到最高点时,线速度的大小为 gl
2
,此时( )
图 7
A.杆受到 1
2
mg 的拉力 B.杆受到 1
2
mg 的压力
C.杆受到 3
2
mg 的拉力 D.杆受到 3
2
mg 的压力
答案 B
解析 以小球为研究对象,小球受重力和沿杆方向杆的弹力,设小球所受弹力方向竖直向下,
则 N+mg=mv2
l
,将 v= gl
2
代入上式得 N=-1
2
mg,即小球在 A 点受杆的弹力方向向上,大
小为 1
2
mg,由牛顿第三定律知杆受到 1
2
mg 的压力.
二、研究运动物体转弯时的向心力
[导学探究] 设火车转弯时的运动为匀速圆周运动.
(1)如果铁路弯道的内外轨一样高,火车在转弯时的向心力由什么力提供?会导致怎样的后
果?
(2)实际上在铁路的弯道处外轨略高于内轨,试从向心力的来源分析这样做有怎样的优点.
(3)当轨道平面与水平面之间的夹角为α,转弯半径为 R 时,火车行驶速度多大轨道才不受挤
压?
(4)当火车行驶速度 v>v0= gRtan α时,轮缘受哪个轨道的压力?当火车行驶速度 vv0= gRtan α时,重力和支持力的合力提供的向心力不足,此时外侧
轨道对轮缘有向里的侧向压力;当火车行驶速度 vv0 时,F 向>F,即所需向心力大于支持力和重力的合力,这时外轨对车轮有侧压力,以
弥补向心力不足的部分.
③当 v 2g
D
C.栗子脱离滚筒的位置与其质量有关
D.若栗子到达最高点时脱离滚筒,栗子将自由下落
答案 A
解析 栗子在最高点恰好不脱离时有:mg=m×D
2
ω2,解得ω= 2g
D
,要求栗子到达滚筒最
高处前与筒壁脱离,则ω< 2g
D
,故 A 正确,B 错误.栗子脱离滚筒的位置与其质量无关,故
C 错误.若栗子到达最高点时脱离滚筒,由于栗子的速度不为零,所以栗子的运动不是自由落
体运动,故 D 错误.故选 A.
课时作业
一、选择题(1~6 题为单选题,7~10 题为多选题)
1.长为 L 的细绳,一端系一质量为 m 的小球,另一端固定于某点,当绳竖直时小球静止,再
给小球一水平初速度 v0,使小球在竖直平面内做圆周运动,并且刚好能过最高点.则下列说法
中正确的是( )
A.小球过最高点时速度为零
B.小球开始运动时绳对小球的拉力为 mv 2
0
L
C.小球过最高点时绳对小球的拉力为 mg
D.小球过最高点时速度大小为 gL
答案 D
解析 小球刚好过最高点时,拉力 T=0,则 mg=mv2
L
,得 v= gL,故 A、C 错误,D 正确;开
始时小球受到的拉力与重力的合力提供向心力,所以:T-mg=mv 2
0
L
,所以 T=mg+mv 2
0
L
,故 B
项错误,故选 D.
2.如图 1 所示,质量相等的汽车甲和汽车乙,以相等的速率沿同一水平弯道做匀速圆周运动,
汽车甲在汽车乙的外侧.两车沿半径方向受到的摩擦力分别为 f 甲和 f 乙.以下说法正确的是
( )
图 1
甲小于 f 乙
甲等于 f 乙
甲大于 f 乙
甲和 f 乙的大小均与汽车速率无关
答案 A
解析 汽车在水平面内做匀速圆周运动,摩擦力提供做匀速圆周运动的向心力,即 f=F 向心
=mv2
r
,由于 r 甲>r 乙,则 f 甲<f 乙,A 正确.
3.如图 2 所示,某公园里的过山车驶过轨道的最高点时,乘客在座椅里面头朝下,人体颠倒,
若轨道半径为 R,人体重为 mg,要使乘客经过轨道最高点时对座椅的压力等于自身的重力,
则过山车在最高点时的速度大小为( )
图 2
错误! 错误! 错误!
答案 C
解析 由题意知 F+mg=2mg=mv2
R
,故速度大小 v= 2gR,C 正确.
4.在铁路转弯处,往往外轨略高于内轨,关于这点下列说法不正确的是( )
A.减轻火车轮子对外轨的挤压
B.减轻火车轮子对内轨的挤压
C.使火车车身倾斜,利用重力和支持力的合力提供转弯所需向心力
D.限制火车向外脱轨
答案 B
5.长度为 1 m 的轻杆 OA 的 A 端有一质量为 2 kg 的小球,以 O 点为圆心,在竖直平面内做圆
周运动,如图 3 所示,小球通过最高点时的速度为 3 m/s,g 取 10 m/s2,则此时小球将( )
图 3
A.受到 18 N 拉力 B.受到 38 N 的支持力
C.受到 2 N 的拉力 D.受到 2 N 的支持力
答案 D
解析 设此时轻杆拉力大小为 F,根据向心力公式有 F+mg=mv2
r
,代入数值可得 F=-2 N,
表示小球受到 2 N 的支持力,选项 D 正确.
6.在高速公路的拐弯处,通常路面都是外高内低.如图 4 所示,在某路段汽车向左拐弯,司机
左侧的路面比右侧的路面低一些.汽车的运动可看做是半径为 R 的圆周运动.设内、外路面高
度差为 h,路基的水平宽度为 d,路面的宽度为 L.已知重力加速度为 g.要使车轮与路面之间
的横向(即垂直于前进方向)摩擦力等于零,则汽车转弯时的车速应等于( )
图 4
错误! 错误! 错误! 错误!
答案 B
解析 设路面的倾角为θ,根据牛顿第二定律得 mgtan θ=mv2
R
,又由数学知识可知 tan θ
=h
d
,联立解得 v= gRh
d
,选项 B 正确.
7.火车转弯可近似看成是做匀速圆周运动,当火车以规定速度通过时,内外轨道均不受侧向
挤压,如图 5.现要降低火车转弯时的规定速度,须对铁路进行改造,从理论上讲以下措施可
行的是( )
图 5
A.减小内外轨的高度差 B.增加内外轨的高度差
C.减小弯道半径 D.增大弯道半径
答案 AC
解析 当火车以规定速度通过弯道时,火车的重力和支持力的合力提供向心力,如图所示:
即 F=mgtan θ,而 F=mv2
R
,故 gRtan θ=v2,若使火车经弯道时的速度 v 减小,则可以减
小倾角θ,即减小内外轨的高度差,或者减小弯道半径 R,故 A、C 正确,B、D 错误.
8.如图 6 所示,一个内壁光滑的弯管处于竖直平面内,其中管道半径为 R. 现有一个半径略
小于弯管横截面半径的光滑小球在弯管里运动,当小球通过最高点时速率为 v0,则下列说法
中正确的是( )
图 6
A.若 v0= gR,则小球对管内壁无压力
B.若 v0> gR,则小球对管内上壁有压力
C.若 0 gR,则有 mg+N=mv 2
0
R
,表明小球对管内上壁有压力,选项 B 正确.
若 0
查看更多