高考数学立体几何大题训练

高考数学立体几何大题训练

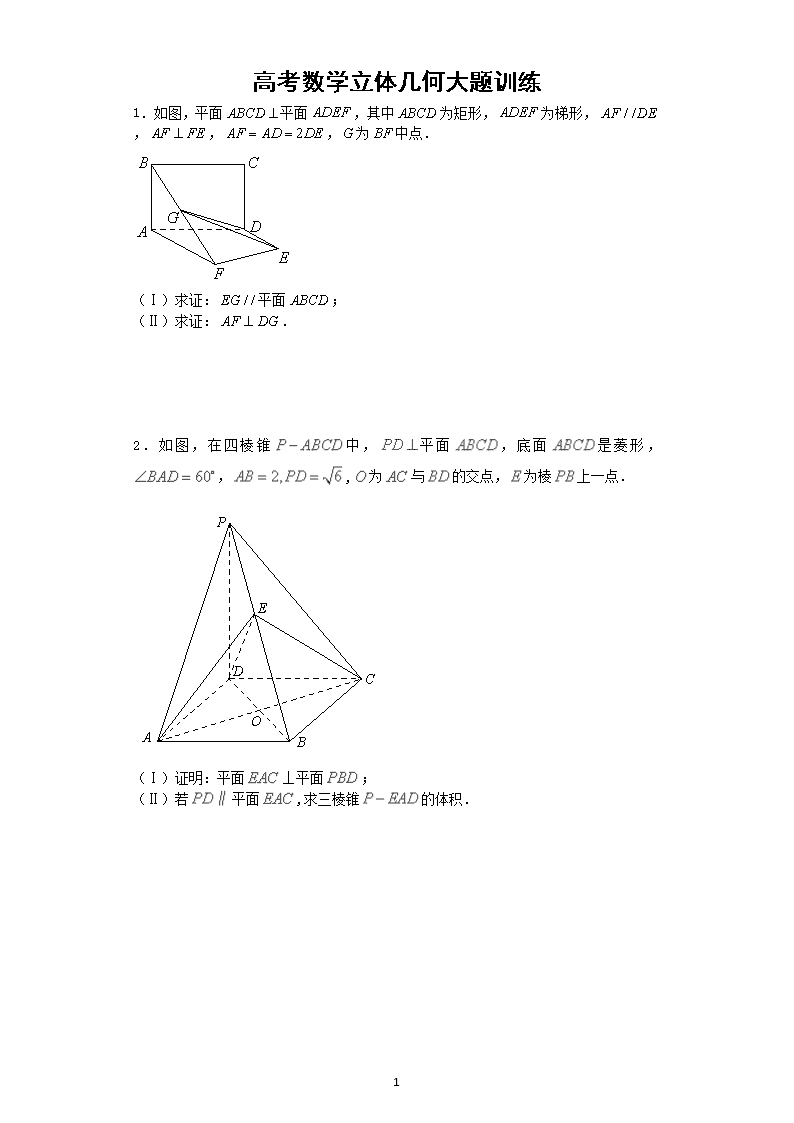
高考数学立体几何大题训练 ‎1．如图，平面平面，其中为矩形，为梯形，，，，为中点．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：．‎ ‎2．如图，在四棱锥中，平面，底面是菱形，，,为与的交点，为棱上一点．‎ P A B C D E O ‎（Ⅰ）证明：平面⊥平面；‎ ‎（Ⅱ）若平面,求三棱锥的体积．‎ 9‎ ‎3．如图，已知四边形ABCD是正方形，平面ABCD，CD=PD=2EA,PD//EA，F，G，H分别为PB，BE，PC的中点.‎ ‎（Ⅰ）求证：GH//平面PDAE；‎ ‎（Ⅱ）求证：平面平面PCD.‎ ‎4．如图，在矩形中，点为边上的点，点为边的中点， ,现将沿边折至位置，且平面平面.‎ ‎ ‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求四棱锥的体积．‎ 9‎ ‎5．如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直，且AB=2，AD=EF=1.‎ ‎（Ⅰ）求证：AF⊥平面CBF；‎ ‎（Ⅱ）设FC的中点为M，求证：OM∥平面DAF；‎ ‎（Ⅲ）设平面CBF将几何体EFABCD分成的两个锥体的体积分别为，求.‎ ‎6．如图所示，在正方体中，分别是棱的中点．‎ E A B C D B1‎ A1‎ D1‎ C1‎ F ‎（Ⅰ）证明：平面平面；‎ ‎（Ⅱ）证明：//平面；‎ ‎（Ⅲ）若正方体棱长为1，求四面体的体积.‎ 9‎ ‎7．如图，四棱锥中，是正三角形，四边形是矩形，且平面平面，，．‎ ‎（Ⅰ）若点是的中点，求证：平面； ‎ ‎（Ⅱ）若点在线段上，且，当三棱锥的体积为时，求实数的值．‎ ‎8．如图，三棱柱中，侧棱垂直底面，，，D是棱的中点.‎ ‎（1）证明：平面；‎ ‎（2）若，求三棱锥的体积.‎ 9‎ ‎9．已知平行四边形，，，，为的中点，把三角形沿折起至位置，使得，是线段的中点.‎ ‎（1）求证：；‎ ‎（2）求证：面面；‎ ‎（3）求四棱锥的体积. ‎ ‎10．如图, 已知边长为2的的菱形与菱形全等，且,平面平面，点为的中点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：；‎ ‎（Ⅲ）求三棱锥的体积.‎ 9‎ ‎11．如图,三棱柱中,,,平面平面,与相交于点.‎ C C1‎ B1‎ A A1‎ B D ‎（Ⅰ）求证:平面；‎ ‎（Ⅱ）求二面角的余弦值.‎ ‎12．如图，已知四边形ABCD为正方形，平面，∥，且 ‎（1）求证：平面；‎ ‎（2）求二面角的余弦值. ‎ 9‎ ‎13．如图，在四棱锥中，底面是正方形，侧面底面， ，点是的中点，点在边上移动．‎ ‎（Ⅰ）若为中点，求证：//平面；‎ ‎（Ⅱ）求证：；‎ ‎（Ⅲ）若，二面角的余弦值等于，试判断点在边上的位置，并说明理由.‎ ‎14．已知几何体的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．‎ ‎（1）求此几何体的体积的大小；‎ ‎（2）求异面直线DE与AB所成角的余弦值；‎ ‎（3）求二面角A-ED-B的正弦值． ‎ 9‎ ‎15．如图，在直三棱柱中，平面侧面，且 ‎（1） 求证：；‎ ‎（2）若直线与平面所成的角为，求锐二面角的大小.‎ ‎16．如图所示，正方形与矩形所在平面互相垂直，，点为的中点.‎ ‎（1）求证：∥平面；（2）求证：；‎ ‎（3）在线段上是否存在点，使二面角的大小为？若存在，求出的长；若不存在，请说明理由.‎ 9‎ ‎17．如图，在三棱柱中，平面，，为棱上的动点，.‎ ‎⑴当为的中点，求直线与平面所成角的正弦值；‎ ‎⑵当的值为多少时，二面角的大小是45.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎18．如图，在四棱锥中，平面平面.‎ ‎（1）证明：平面;‎ ‎（2）求二面角的大小 9‎ ‎19．如图，正方形与梯形所在的平面互相垂直，，∥，，，为的中点．‎ ‎（1）求证：∥平面；‎ ‎（2）求证：平面平面；‎ ‎（3）求平面与平面所成锐二面角的余弦值.‎ ‎20．在如图所示的几何体中，四边形为平行四边形，，平面，，，，.‎ ‎（1）若是线段的中点，求证：平面；‎ ‎（2）若，求二面角的余弦值.‎ 9‎ 参考答案 ‎1．（Ⅰ）详见解析; （Ⅱ）详见解析 ‎【解析】‎ 试题分析：证明：（Ⅰ）取的中点，连接，可得， 又因为，‎ 所以，四边形为平行四边形，所以 ，在根据线面平行的判定定理，即可证明结果．（Ⅱ）取的中点，连接、，可得， 因为平面平面，，所以平面，，所以，因为，‎ 所以四边形为平行四边形，，又，所以 ，根据线面垂直的判定定理，即可证明结果．‎ 试题解析：证明：（Ⅰ）取的中点，连接 因为分别是,的中点，‎ 所以， 2分 又因为，‎ 所以，四边形为平行四边形 所以 4分 因为平面，平面 所以平面 5分 ‎（Ⅱ）取的中点，连接、‎ 因为分别是,的中点，‎ 所以， 7分 因为平面平面，‎ 所以平面，‎ 所以 9分 因为，‎ 所以四边形为平行四边形，‎ 又，所以 11分 因为 所以平面 37‎ 所以 12分 考点： 1．线面平行的判定定理；2．线面垂直的判定定理．‎ ‎2．（Ⅰ）证明见解析；（Ⅱ）．‎ ‎【解析】‎ 试题分析：（Ⅰ）要证面面垂直需证线面垂直，根据题意，需证平面，因为底面为菱形对角线互相垂直，又因为平面，所以平面得证；（Ⅱ）根据线面平行的性质定理可知：平行平面与平面的交线,同时为中点,所以为中点，所以三棱锥的体积等于三棱锥即为三棱锥体积的一半,进而求得三棱锥的体积．‎ 试题解析：（Ⅰ）平面,平面,．‎ 四边形是菱形,,又,平面．‎ 而平面,平面⊥平面． 6分 ‎（Ⅱ）平面,平面平面,,‎ 是中点,是中点．‎ P A B C D E O H 取中点,连结,四边形是菱形,,‎ ‎,又,平面,‎ ‎． 9分 ‎． 12分 考点：1．面面平行的判定定理;2．线面平行的性质定理;3．三棱锥的体积公式．‎ 37‎ ‎3．（1）证明详见解析；（2）证明详见解析.‎ ‎【解析】‎ 试题分析：本题主要考查线线平行、线面平行、线线垂直、线面垂直等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑思维能力、计算能力.第一问，取PD、EA中点，利用中位线得，，而，∴，∴说明是平行四边形，∴，∴利用线面平行的判定平面；第二问，先利用线面垂直的性质得，再利用线面垂直的判定得平面，即平面，最后利用面面垂直的判定得平面平面.‎ 试题解析：（1）分别取的中点的中点连结.‎ 因为分别为的中点，所以 .‎ 因为，所以,‎ 故四边形是平行四边形.所以. 4分 又因为平面，平面，‎ 所以平面. 6分 ‎（2）证明：因为平面，平面，所以.‎ 因为所以平面.‎ 因为分别为的中点，所以 所以平面 因为平面，所以平面平面. 12分 考点：线线平行、线面平行、线线垂直、线面垂直.‎ ‎4．（Ⅰ）见解析（Ⅱ）‎ ‎【解析】‎ 试题分析：对于第一问要证明面面垂直，关键是把握住面面垂直的判定定理，在其中一个平面内找出另一个平面的垂线即可，而在找线面垂直时，需要把握住线面垂直的判定定理的内容，注意做好空间中的垂直转化工作，对于第二问，注意在求棱锥的体积时，注意把握住有关求体积的量是多少，底面积和高弄清楚后就没有问题.‎ 试题解析：（Ⅰ）证明：在中,‎ 37‎ 在中，,‎ ‎,. 3分 平面平面，且平面平面 ‎ 平面,‎ 平面，平面平面. 6分 ‎（Ⅱ）解：过做,‎ 平面平面平面且平面平面 ‎ 平面,‎ 四棱锥的高. 8分 ‎ ‎ ‎ 10分 则. 12分 考点：面面垂直的判定，棱锥的体积.‎ ‎5．（Ⅰ）参考解析；（Ⅱ）参考解析；（Ⅲ）‎ ‎【解析】‎ 试题分析：（Ⅰ）要证线面垂直等价转化为线线垂直，由圆周角所对的弦为直径即可得AF与BF垂直，再根据面面垂直的性质即可得CB与AF垂直.由此即可得到结论.‎ ‎（Ⅱ）线面平行等价转化为线线平行，通过做DF的中点即可得到一个平行四边形，由此即可得到线线平行，即可得到结论.‎ ‎（Ⅲ）根据四棱锥的体积公式，以及三棱锥的体积公式，其中有些公共的线段，由此即可求出两个体积的比值.‎ 试题解析：（Ⅰ）证明：∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，‎ ‎∴CB⊥平面ABEF，∵AF平面ABEF，∴AF⊥CB， ‎ 又∵AB为圆O的直径，∴AF⊥BF，∴AF⊥平面CBF.‎ ‎（Ⅱ）设DF的中点为N，则MN，又，‎ 则，MNAO为平行四边形， ‎ 37‎ ‎∴OM∥AN，又AN平面DAF，PM平面DAF，∴OM∥平面DAF.‎ ‎（Ⅲ）过点F作FG⊥AB于G，∵平面ABCD⊥平面ABEF，‎ ‎∴FG⊥平面ABCD，∴， ‎ ‎∵CB⊥平面ABEF，∴，‎ ‎∴‎ 考点：1.线面垂直.2.线面平行.3.棱锥的体积公式.‎ ‎6．（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）‎ ‎【解析】‎ 试题分析：Ⅰ）证明面面垂直，一般利用面面垂直判定定理，即从证明线面垂直出发：因为面所以．又，所以面,所以平面面.（Ⅱ）证明线面平行，一般利用线面平行判定定理，即从证明线线平行出发，这一般可利用平面几何知识得以证明：设，则易得四边形为平行四边形，所以//.所以//面 （Ⅲ）求棱锥体积，关键在于确定其高。可以利用等体积法将其转化为可确定高的棱锥：‎ 试题解析：（Ⅰ）证明: ‎ 因为为正方体，‎ 所以面；‎ 因为面，所以． 2分 又因为，，所以面 ‎ 因为面,所以平面面. 5分 ‎（Ⅱ）连接,//，且， ‎ 37‎ E F A B C D B1‎ A1‎ D1‎ C1‎ 设，‎ 则//且,‎ 所以//且，‎ 所以四边形为平行四边形. 所以//. 9分 又因为，．‎ 所以//面 11分 ‎（Ⅲ） 14分 考点：面面垂直判定定理，线面平行判定定理，棱锥体积 ‎7．（Ⅰ）证明见解析；（Ⅱ）‎ ‎【解析】‎ 试题分析：（Ⅰ）将证明线面平行转化为线线平行，通过做辅助线可证明出//，线面平行的判定定理可证出平面；（Ⅱ）如图所示作辅助线，通过题意可先分将问题转化为求，由面面垂直的性质定理得平面，进而平面，得到平面，故，进而确定，再由 37‎ 试题解析：（Ⅰ）如图，连接，设，又点是的中点，‎ 则在中，中位线//， 3分 又平面，平面．‎ 所以平面 5分 ‎ ‎ ‎（Ⅱ）依据题意可得：，取中点，所以，且 又平面平面，则平面； 6分 作于上一点，则平面，‎ 因为四边形是矩形，所以平面，‎ 则为直角三角形 8分 所以，则直角三角形的面积为 ‎ ‎ 10分 由得： 12分 考点：1、线面平行问题与线线平行问题的互化；2、面面垂直与线面垂直问题的互化；3、综合分析能力．‎ ‎8．（1）见解析 （2）‎ ‎【解析】‎ 试题分析：对应第一问，关键是要掌握线面垂直的判定，把握线线垂直的证明方法，第二问注意椎体的体积公式的应用.‎ 试题解析：（1）由题设知，，‎ ‎∴平面. （2分）‎ 37‎ 又∵平面，∴. （3分）‎ 由题设知，∴，即. （4分）‎ ‎∵，∴平面. （6分）‎ ‎（2） ∵，D是棱的中点，‎ ‎∴ （7分）‎ ‎∴， （9分）‎ ‎∴的面积 （10分）‎ ‎∴ （11分）‎ ‎∴，即三棱锥的体积为. （13分）‎ 考点：线面垂直的判定，椎体的体积.‎ ‎9．（1）证明见解析；（2）证明见解析；（3）3.‎ ‎【解析】‎ 试题分析：（1）此题将线面平行转化为线线平行问题，可取的中点，连接构造辅助线，得到，进而证明出平面；（2）此题将面面垂直问题转化为线面垂直问题，可取的中点，连接构造辅助线,借助于余弦定理，得出，即为直角三角形，由线面垂直的判定定理，证明出，根据面面垂直的判定定理得出面面；‎ ‎（3）由棱锥的体积公式得，梯形的底边为2、4，高为，由（2），代入上式即可求得.‎ 试题解析： (1)证明：取的中点，连接 37‎ ‎ 为中点 ‎，且 ‎ ‎ 为平行四边形边的中点 ‎，且 ‎ ‎，且 四边形是平行四边形 平面，平面 ‎ 平面 4分 ‎（2）取的中点，连接 ‎，，，为的中点 为等边三角形，即折叠后也为等边三角形 ‎，且 在中，，，‎ 37‎ 根据余弦定理，可得 在中，，，，‎ ‎，即 又，所以 又 面面 10分 ‎（3）由第（2）问知 ‎3‎ ‎ 14分 考点：1、线面平行；2、面面垂直；3.棱锥的体积 ‎10．（Ⅰ）见解析；（Ⅱ）见解析； （Ⅲ）‎ ‎【解析】‎ 试题分析：（Ⅰ）要证明线面平行，只需证明这条直线以平面内的一条直线平行即可，连结,易得为三角形的中位线，所以，，平面；要证明线线垂直，一般通过线面垂直得到，易得平面，，在菱形中，平面 ‎（Ⅲ）利用等体积法即可，即 ‎ 试题解析：（Ⅰ）连结, ..1分 因为四边形是菱形，‎ 所以，,又,‎ 37‎ 所以，为三角形的中位线 .2分 所以，.‎ 又平面,平面 平面 4分 ‎ ‎（Ⅱ）因为四边形是菱形，所以。‎ 又平面平面，且交线为 平面, 2分 又 平面 ‎ 3分 在菱形中，,‎ ‎ 4分 平面 平面 5分 ‎ 6分 ‎（Ⅲ）由题知，=2,故,‎ 在三角形中，,,所以=. 1分 又,所以,所以是等边三角形，‎ 所以,‎ 所以 2分 又面，所以，点C到面的距离 3分 所以 4分 考点：立体几何的综合应用 ‎11．（Ⅰ）见解析 ；（Ⅱ）‎ ‎【解析】‎ 试题分析：（Ⅰ）证明直线和平面垂直的常用方法：（1）利用判定定理．（2）利用判定定理的推论（）．（3）利用面面平行的性质（）．（4）利用面面垂直的性质．本题即是利用面面垂直的性质；（Ⅱ）求面面角方法一是传统方法，作出二面角，难度较大，一般不采用，方法二是向量法，思路简单，运算量稍大，一般采用向量法.‎ 试题解析：（Ⅰ）依题意,侧面是菱形,是的中点,因为,所以,‎ 又平面平面,且平面,平面平面 37‎ 所以平面. 5分 ‎（Ⅱ）[传统法]由（Ⅰ）知平面,面,所以,‎ C C1‎ B1‎ A A1‎ B D H 传统法图 又,,所以平面,‎ 过作,垂足为,连结,则,‎ 所以为二面角的平面角. 9分 在中,,‎ 所以, 12分 所以,即二面角的余弦值是. 14分 ‎[向量法]以为原点,建立空间直角坐标系如图所示, 6分 C1‎ B1‎ A C A1‎ B D x z y 向量法图 由已知可得 ‎ 故,‎ 则, 8分 设平面的一个法向量是,‎ 37‎ 则,即,解得 令,得 11分 显然是平面的一个法向量, 12分 所以,即二面角的余弦值是. 14分 考点：线面垂直、二面角 ‎12．（1）详见解析；（2）二面角的余弦值为 .‎ ‎【解析】‎ 试题分析：（1） 因为EA∥CF，所以ACFE是一个平面图形，在这个平面图形中，AC＝AE＝2，所以ΔACE是等腰直角三角形.连接AC交BD于点O，连接FO.易得OC＝FC，所以ΔOCF也是等腰直角三角形.由此可证得EC⊥OF.又由三垂线定理可证得，从而可得平面.法二，‎ ‎ 以点A为坐标原点，AD所在的直线为x轴，AB所在直线为y轴，AE所在直线为z轴建立直角坐标系，利用向量也可证得面.（2）由（1）知向量为平面的法向量，再用向量方法求出平面的法向量即可求出二面角的余弦值.‎ 试题解析：（1）（法一）连接AC交BD于点O，连接FO.过点O作OH∥AE交EC于点H，连接HF，因为O是AC的中点，所以H是EC的中点，所以，因为EA∥CF，且EA=2CF，所以OH∥CF且OH=CF，又因为 所以四边形OCFH为菱形，而垂直于平面ABCD，‎ 所以从而，从而四边形OCFH 为正方形进而 又因为四边形ABCD为正方形，所以; 又 且从而面，‎ 则 又且所以平面. ..............6分 ‎（法二）‎ ‎ 以点A为坐标原点，AD所在的直线为x轴，AB所在直线为y轴，AE所在直线为z轴建立直角坐标系，则 ‎，‎ 所以 37‎ 从而有·=0，·=0‎ 所以 又因为从而面 ‎ ‎（2）由（1）知向量为平面的法向量 设平面的法向量为 则即；令得 故 ‎ 所以二面角的余弦值为 ‎ 考点：1、空间线面间的位置关系；2、二面角.‎ ‎13．（1）证明详见解析；（2）证明详见解析；（3）点F为边BC上靠近B点的三等分点.‎ ‎【解析】‎ 试题分析：本题主要考查线线平行、线面平行、线线垂直、线面垂直、二面角、向量法等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力.第一问，在中，E、F分别是BP、BC中点，利用中位线的性质得，再根据线面平行的判定得出结论；第二问，由正方形ABCD得出，利用面面垂直的性质，得平面PAB，利用线面垂直的性质，得，再从中证出，利用线面垂直的判定得平面PBC，所以AE垂直面PBC内的线PF；第三问，利用已知的这些条件整理出AD、AB、AP两两垂直，建立空间直角坐标系，写出相关点的坐标，得出向量坐标，分别求出平面AEF和平面ABF的法向量，利用夹角公式列出表达式，求出m，即得到BF的长，从而得到点F的位置.‎ 试题解析：（1）在中，∵点E是PB中点，点F是BC中点，‎ ‎∴，‎ 又∵平面PAC，平面PAC，‎ ‎∴平面PAC．‎ ‎（2）∵底面ABCD是正方形，∴.‎ 又∵侧面PAB底面ABCD，平面PAB平面ABCD=AB，且平面ABCD，‎ ‎∴平面PAB.‎ ‎∵平面PAB，‎ ‎∴，‎ 由已知，点E是PB的中点，‎ ‎∴，‎ 又∵，‎ ‎∴平面PBC.‎ 37‎ ‎∵平面PBC，‎ ‎∴.‎ ‎（3）点F为边BC上靠近B点的三等分点.‎ ‎∵，，‎ ‎∴，‎ 由（2）可知，平面PAB.‎ 又，‎ ‎∴平面PAB，即，‎ ‎∴两两垂直.‎ 分别以AD，AB，AP为x轴，y轴，z轴，建立空间直角坐标系（如图）.‎ 不妨设，则，.‎ ‎∴，.‎ 设平面AEF的一个法向量为，‎ ‎∵，得，取，则，，得.‎ ‎∵，，，‎ ‎∴平面ABCD.‎ 即平面ABF的一个法向量为.‎ ‎∴，解得.‎ 37‎ ‎∵，‎ ‎∴，即点F为边BC上靠近B点的三等分点.‎ 考点：线线平行、线面平行、线线垂直、线面垂直、二面角、向量法.‎ ‎14．（1）16；（2） ；（3）．‎ ‎【解析】‎ 试题分析：（1）由三视图易得AC⊥平面BCE，则体积；（2）取EC的中点是F，连结BF，可证∠FBA或其补角即为异面直线DE与AB所成的角，在△BAF中，利用余弦定理可求得异面直线DE与AB所成的角的余弦值为 ；（3）过C作CG⊥DE交DE于G，连AG，可证DE⊥平面ACG，‎ 易知∠AGC为二面角A-ED-B的平面角，在△ACG中，可求得二面角A-ED-B的的正弦值为．‎ 试题解析：（1）AC⊥平面BCE， 则 ‎ ‎∴几何体的体积V为16．‎ ‎（2）取EC的中点是F，连结BF，则BF//DE，∴∠FBA或其补角即为异面直线DE与AB所成的角．‎ 在△BAF中，AB=，BF=AF=．∴．‎ ‎∴异面直线DE与AB所成的角的余弦值为 ‎ ‎（3）AC⊥平面BCE，过C作CG⊥DE交DE于G，连AG．可得DE⊥平面ACG，‎ 从而AG⊥DE,∴∠AGC为二面角A-ED-B的平面角．‎ 在△ACG中，∠ACG=90°，AC=4，ＣG=,∴．∴．‎ ‎∴二面角A-ED-B的的正弦值为．‎ 37‎ 考点：1．空间几何体的结构特征与三视图；2．空间几何中的线面角与二面角 ‎15．（1）详见解析；（2）‎ ‎【解析】‎ 试题分析：（1） 取的中点，连接，要证 ,只要证 平面 ‎ 由直三棱柱的性质可知 ,只需证，因此只要证明平面 事实上，由已知平面侧面，平面，且 所以平面成立，于是结论可证.‎ ‎（2） 思路一：连接，可证即为直线与所成的角，则 ‎ 过点A作于点，连，可证即为二面角的一个平面角.在直角中 ，即二面角的大小为 思路二：以点为原点，以所在直线分别为轴建立空间直角坐标系 设平面的一个法向量，平面的一个法向量为，利用向量的数量积求出这两个法向量的坐标，进而利用法向量的夹角求出锐二面角的大小.‎ 试题解析：.解（1）证明：如图，取的中点，连接，‎ 因，则 由平面侧面，且平面侧面，‎ 得，又平面， 所以.‎ 因为三棱柱是直三棱柱，则，所以.‎ 又，从而侧面 ，又侧面，故.‎ 37‎ 解法一：连接，由（1）可知，则是在内的射影 ‎∴ 即为直线与所成的角，则 在等腰直角中，，且点是中点，∴ ，且， ∴ ‎ 过点A作于点，连，由（1）知，则，且 ‎∴ 即为二面角的一个平面角 且直角中：，又，‎ ‎∴ ，‎ 且二面角为锐二面角 ∴ ，即二面角的大小为 ‎ 解法二（向量法）：由（1）知且，所以以点为原点，以 37‎ 所在直线分别为轴建立空间直角坐标系，如图所示，且设，则，，，，，，， ‎ ‎ ‎ 设平面的一个法向量，由， 得：‎ ‎ 令 ，得 ，则 ‎ 设直线与所成的角为，则 得，解得，即 ‎ 又设平面的一个法向量为，同理可得，‎ 设锐二面角的大小为，则 ‎，且，得 ‎ ‎∴ 锐二面角的大小为. ‎ 考点：1、空间直线、平面的位置关系；2、空间向量在立体几何问题中的应用.‎ 37‎ ‎16．（1)祥见解析；（2）祥见解析；（3）存在满足条件的.‎ ‎【解析】‎ 试题分析：（1）O是AD1的中点，连接OE，由中位线定理可得EO∥BD1，再由线面平行的判定定理可得BD1∥平面A1DE；‎ ‎（2）由正方形AA1D1D与矩形ABCD所在平面互相垂直，根据面面垂直的性质定理可得AB⊥平面ADD1A1，进而线面垂直的性质定理得到AB⊥A1D，结合A1D⊥AD1及线面垂直的判定定理，可得A1D⊥平面AD1E，进而D1E⊥A1D；‎ ‎（3）以点D为原点，DA，DC，DD1所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，设M（1，a，0）（0≤a≤2），分别求出平面D1MC的法向量和平面MCD的一个法向量，根据二面角D1-MC-D的大小为，结合向量夹角公式，构造关于a的方程，解方程可得M点的坐标，进而求出AM长．‎ 试题解析：（1)连结交于，连结,因为四边形为正方形，所以为的中点，又点为的中点，在中，有中位线定理有//，而平面，平面，‎ 所以，//平面.‎ ‎（2）因为正方形与矩形所在平面互相垂直，所以，，‎ 而，所以平面，又平面，所以.‎ ‎（3）存在满足条件的.‎ 依题意，以为坐标原点，、、分别为轴、轴、轴建立空间直角坐标系，因为，则，，，，，所，‎ 易知为平面的法向量，设，所以平面的法向量为，所以，即，所以 37‎ ‎，取，‎ 则，又二面角的大小为，‎ 所以，解得.‎ 故在线段上是存在点，使二面角的大小为，且.‎ 考点：1．空间中直线与直线之间的位置关系；２．直线与平面平行的判定；３．空间向量求平面间的夹角.‎ ‎17．（1），（2）.‎ ‎【解析】‎ 试题分析：（1）此小题考查用空间向量解决线面角问题，只需找到面的法向量与线的方向向量，注意用好如下公式：，且线面角的范围为：；（2）此小题考查的是用空间向量解决面面角问题，只需找到两个面的法向量，但由于点坐标未知，可先设出，利用二面角的大小是45，求出点坐标，从而可得到的长度，则易求出其比值.‎ 试题解析：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 如图，以点为原点建立空间直角坐标系，依题意得，⑴因为为中点，则，‎ 37‎ 设是平面的一个法向量，则，得，取，则，设直线与平面的法向量的夹角为，则，所以直线与平面所成角的正弦值为；‎ ‎⑵设，设是平面的一个法向量，则，取，则，是平面的一个法向量，，得，即，所以当时，二面角的大小是.‎ 考点：运用空间向量解决线面角与面面角问题，要掌握线面角与面面角的公式，要注意合理建系.‎ ‎18．（1）详见解析；（2）二面角的大小是．‎ ‎【解析】‎ 试题分析：（1）求证：平面，证明线面垂直，先证线线垂直，即证线和平面内两条相交直线垂直，由已知可得，只需证明，或，由已知平面平面，只需证明，就得平面，即，而由已知，在直角梯形中，易求，从而满足，即得，问题得证；（2）求二面角的大小，可用传统方法，也可用向量法，用传统方法，关键是找二面角的平面角，可利用三垂线定理来找，但本题不存在利用三垂线定理的条件，因此利用垂面法，即作，与交于点，过点作，与交于点，连结，由（1）知，，则，，所以是二面角的平面角，求出 37‎ 的三条边，利用余弦定理，即可求出二面角的大小，用向量法，首先建立空间坐标系，先找三条两两垂直的直线作为坐标轴，观察几何图形可知，以为原点，分别以射线为轴的正半轴，建立空间直角坐标系，写出个点坐标，设出设平面的法向量为，平面的法向量为，求出它们的一个法向量，利用法向量的夹角与二面角的关系，即可求出二面角的大小．‎ ‎（1）在直角梯形中，由，得，，由，则，即，又平面平面，从而平面，所以，又，从而平面；‎ ‎（2）方法一：作，与交于点，过点作，与交于点，连结，由（1）知，，则，，所以是二面角的平面角，在直角梯形中，由，得，又平面平面，得平面，从而，，由于平面，得：，在中，由，，得，‎ 在中，，，得，在中，，，，得，，从而，在中，利用余弦定理分别可得，在中，，所以，即二面角的大小是．‎ 37‎ 方法二：以为原点，分别以射线为轴的正半轴，建立空间直角坐标系如图所示，由题意可知各点坐标如下：，设平面的法向量为，平面的法向量为，可算得，，由得，，可取，由得，，可取，于是，由题意可知，所求二面角是锐角，故二面角的大小是．‎ 点评：本题主要考查空间点，线，面位置关系，二面角等基础知识，空间向量的应用 ，同时考查空间想象能力，与推理论证，运算求解能力．‎ ‎19．（1）证明过程详见解析；（2）证明过程详见解析；（3）.‎ ‎【解析】‎ 试题分析：本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力.第一问，作出辅助线MN，N为中点，在中，利用中位线得到，且，结合已知条件，可证出四边形ABMN为平行四边形，所以，利用线面平行的判定，得∥平面；第二问，利用面面垂直的性质，判断面，再利用已知的边长，可证出，则利用线面垂直的判定得平面BDE，再利用面面垂直的判定得平面平面；第三问，可以利用传统几何法证明二面角的平面角，也可以利用向量法建立空间直角坐标系，求出平面BEC和平面ADEF的法向量，利用夹角公式计算即可.‎ 37‎ ‎（1）证明：取中点，连结．‎ 在△中，‎ 分别为的中点，所以∥，且 ‎．由已知∥，，所以 ‎∥，且．所以四边形为平行四边形，‎ 所以∥．‎ 又因为平面，且平面，‎ 所以∥平面． 4分 ‎（2）证明：在正方形中，．又因为 平面平面，且平面平面，‎ 所以平面．所以． 6分 在直角梯形中，，，可得．‎ 在△中，，所以． 7分 所以平面． 8分 又因为平面，所以平面平面． 9分 ‎（3）（方法一）延长和交于．‎ 在平面内过作于,连结．由平面平面，‎ ‎∥，，平面平面=，‎ 得，于是．‎ 37‎ 又，平面，所以，‎ 于是就是平面与平面所成锐二面角的 平面角. 12分 由，得.‎ 又，于是有.‎ 在中，.‎ 所以平面与平面所成锐二面角的余弦值为． 14分 ‎（方法二）由（2）知平面，且． ‎ ‎ 以为原点，所在直线分别为轴，建立空间直角坐标系．‎ 易得 .平面的一个法向量为.设为平面的一个法向量，因为，所以，令，得．‎ 所以为平面的一个法向量． １２分 ‎ 设平面与平面所成锐二面角为． ‎ 则．所以平面与平面 37‎ 所成锐二面角的余弦值为． 14分 考点：中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角.‎ ‎20．（1）详见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）连接，利用平行线的传递性结合得到，再利用点为的中点得到，从而证明四边形为平行四边形，从而得到，最终结合直线与平面的判定定理证明平面；（2）建立以点为坐标原点，以、、所在直线为轴、轴、轴的空间直角坐标系，利用空间向量法来求二面角的余弦值.‎ 试题解析：（1），，，，‎ ‎，，‎ 由于，因此连接，由于，，‎ 在平行四边形中，是线段的中点，则，且，‎ 因此，且，所以四边形为平行四边形，，‎ 又平面，平面，平面；‎ ‎（2），，‎ 又平面，、、两两垂直。‎ 分别以、、所在直线为轴、轴、轴建立如图所示的空间直角坐标系，‎ 37‎ 则、、、，‎ 故，，又，，.‎ 设平面的法向量，‎ 则，，取，得，所以，‎ 设平面的法向量，则 ‎，∴，取，得，所以，‎ 所以 故二面角的余弦值为.‎ 考点：1.直线与平面平行；2.利用空间向量法求二面角 37‎