高考数学理二轮专练五压轴大题目一

高考数学理二轮专练五压轴大题目一

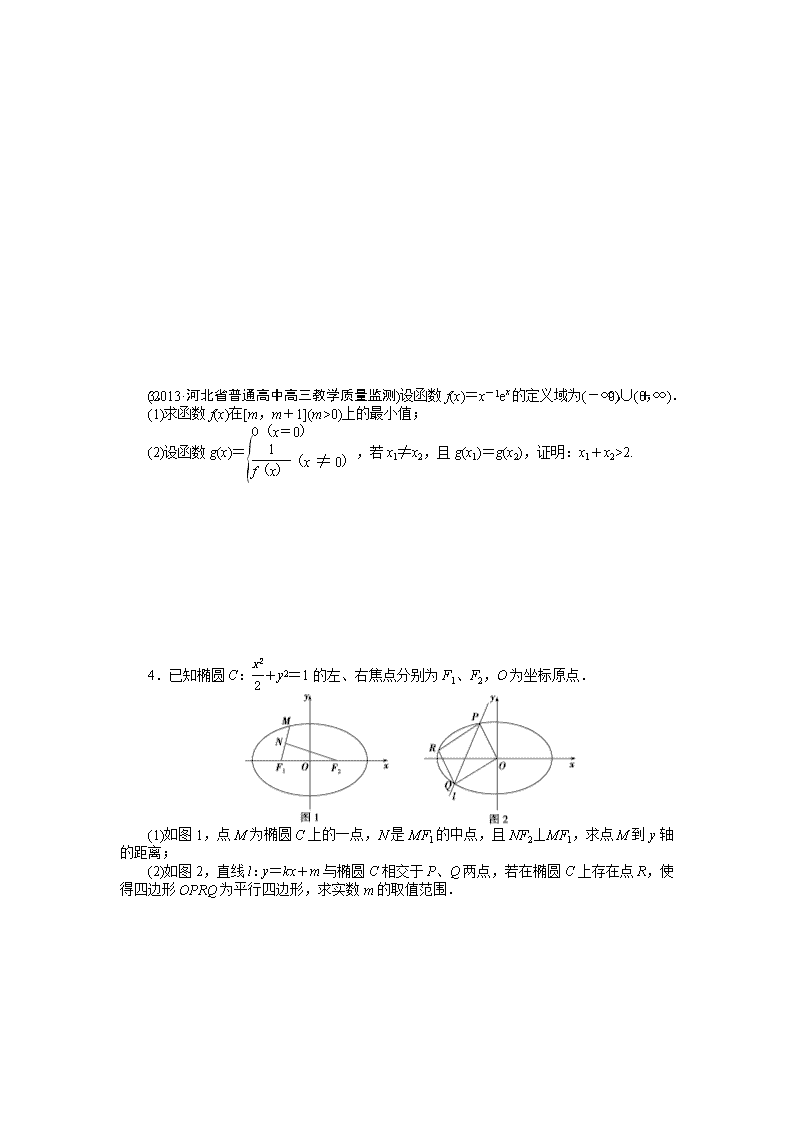
压轴大题(一)‎ ‎1．(2013·广东省惠州市高三第三次调研考试)已知函数f(x)＝x3－3ax(a∈R)．‎ ‎(1)当a＝1时，求f(x)的极小值；‎ ‎(2)若对任意的m∈R，直线x＋y＋m＝0都不是曲线y＝f(x)的切线，求a的取值范围．‎ ‎2．(2013·北京市海淀区高三年级第二学期期中练习)已知圆M：(x－)2＋y2＝r2(r>0)．若椭圆C：＋＝1(a>b>0)的右顶点为圆M的圆心，离心率为.‎ ‎(1)求椭圆C的方程；‎ ‎(2)若存在直线l：y＝kx，使得直线l与椭圆C分别交于A，B两点，与圆M分别交于G，H两点，点G在线段AB上，且|AG|＝|BH|，求圆M的半径r的取值范围．‎ ‎3．(2013·河北省普通高中高三教学质量监测)设函数f(x)＝x－1ex的定义域为(－∞，0)∪(0，＋∞)．‎ ‎(1)求函数f(x)在[m，m＋1](m>0)上的最小值；‎ ‎(2)设函数g(x)＝，若x1≠x2，且g(x1)＝g(x2)，证明：x1＋x2>2.‎ ‎ ‎ ‎ ‎ ‎4．已知椭圆C：＋y2＝1的左、右焦点分别为F1、F2，O为坐标原点．‎ ‎(1)如图1，点M为椭圆C上的一点，N是MF1的中点，且NF2⊥MF1，求点M到y轴的距离；‎ ‎(2)如图2，直线l：y＝kx＋m与椭圆C相交于P、Q两点，若在椭圆C上存在点R，使得四边形OPRQ为平行四边形，求实数m的取值范围．‎ 答案：‎ ‎1．【解】(1)当a＝1时，f′(x)＝3x2－3，‎ 令f′(x)＝0，得x＝－1或x＝1，‎ 当x∈(－1，1)时，f′(x)<0，当x∈(－∞，－1)∪(1，＋∞)时，f′(x)>0，‎ ‎∴f(x)在(－1，1)上单调递减，在(－∞，－1)，(1，＋∞)上单调递增，‎ ‎∴f(x)的极小值是f(1)＝－2.‎ ‎(2)f′(x)＝3x2－3a，直线x＋y＋m＝0即y＝－x－m，‎ 依题意，切线斜率k＝f′(x)＝3x2－3a≠－1，‎ 即3x2－3a＋1＝0无解，‎ ‎∴Δ＝0－4×3(－3a＋1)<0，‎ ‎∴a<.‎ 故a的取值范围是(－∞，)．‎ ‎2．【解】(1)设椭圆的焦距为2c，‎ 因为a＝，＝，所以c＝1，所以b＝1.‎ 所以椭圆C的方程为＋y2＝1.‎ ‎(2)设A(x1，y1)，B(x2，y2)，‎ 联立方程得，‎ 所以(1＋2k2)x2－2＝0，则x1＋x2＝0，x1x2＝－.‎ 所以|AB|＝＝.‎ 又点M(，0)到直线l的距离d＝，‎ 则|GH|＝2 ，‎ 显然，若点H也在线段AB上，则由对称性可知，直线y＝kx就是y轴，与已知矛盾，‎ 所以要使|AG|＝|BH|，‎ 只要|AB|＝|GH|，‎ 所以＝4(r2－)，‎ r2＝＋ ‎＝ ‎＝2(1＋)．‎ 当k＝0时，r＝.‎ 当k≠0时，r2＝2(1＋)<2(1＋)＝3，‎ 又显然r2＝2(1＋)>2，所以1时，f′(x)>0；‎ ‎01时，2x－2>0，从而e2x－2－1>0.‎ 又e－x>0，所以F′(x)>0，‎ 从而函数F(x)在[1，＋∞)上是增函数．‎ 又F(1)＝e－1－e－1＝0，所以x>1时，‎ 有F(x)>F(1)＝0，‎ 即g(x)>g(2－x)．②‎ 由①及g(x1)＝g(x2)，知x1与x2只能在1的两侧．‎ 不妨设01，‎ 由结论②可知，g(x2)>g(2－x2)，‎ 所以g(x1)＝g(x2)>g(2－x2)．‎ ‎ 因为x2>1，所以2－x2<1.‎ 又由结论①可知函数g(x)在(－∞，1)内是增函数，‎ 所以x1>2－x2，即x1＋x2>2.‎ ‎4．【解】(1)由题意知，F1(－1，0)，F2(1，0)，‎ 设M(x0，y0)，∵N为MF1的中点，∴N(，)，‎ ‎∴＝(－1－x0，－y0)，＝(，－)，‎ ‎∵MF1⊥NF2，∴·＝0，‎ 即(－1－x0，－y0)·(，－)＝0，‎ ‎∴x－2x0－3＋y＝0，①‎ 又有＋y＝1，②‎ 由①②解得x0＝2－2(x0＝2＋2舍去)，‎ ‎∴点M到y轴的距离为2－2.‎ ‎(2)设P(x1，y1)，Q(x2，y2)，R(xR，yR)，‎ ‎∵四边形OPRQ为平行四边形，‎ ‎∴x1＋x2＝xR，y1＋y2＝yR.‎ ‎∵点R在椭圆上，∴＋(y1＋y2)2＝1，‎ 即＋[k(x1＋x2)＋2m]2＝1，‎ 化简得，(1＋2k2)(x1＋x2)2＋8km(x1＋x2)＋8m2＝2.③‎ 由得(1＋2k2)x2＋4kmx＋2m2－2＝0.‎ 由Δ>0，得2k2＋1>m2，④‎ 由根与系数的关系得， x1＋x2＝－，‎ 代入③式，得－＋8m2＝2，‎ 化简得4m2＝1＋2k2，代入④式，得m≠0.‎ 又4m2＝1＋2k2≥1，∴m≤－或m≥.‎ 故实数m的取值范围是(－∞，－]∪[，＋∞)．‎