高考全国2卷理科数学试题含解析

高考全国2卷理科数学试题含解析

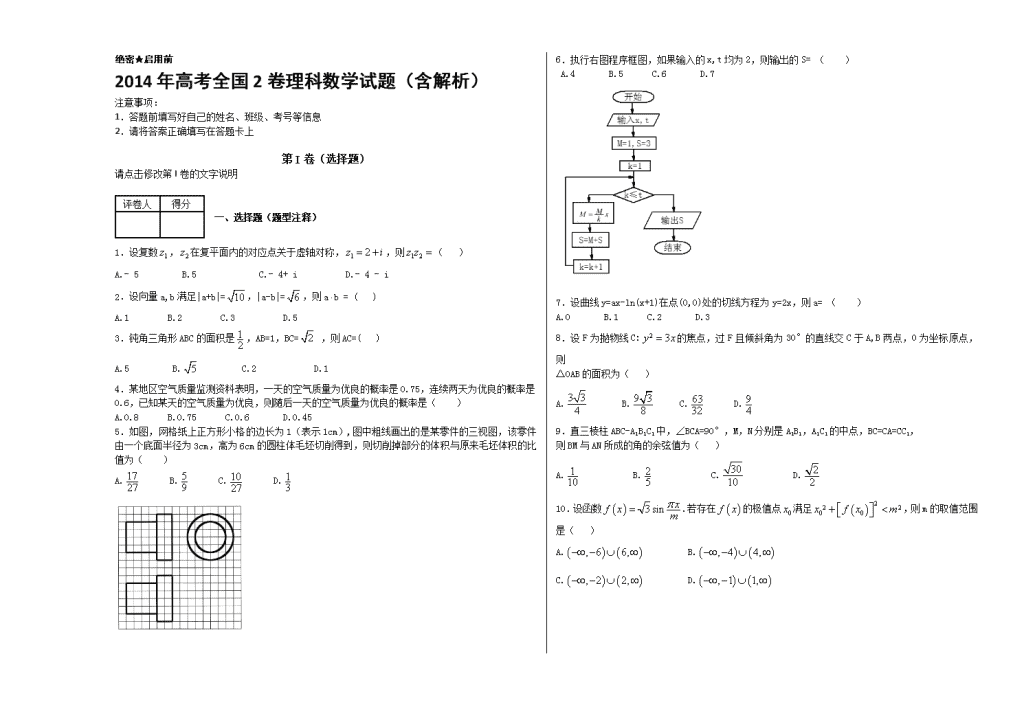
绝密★启用前 ‎2014年高考全国2卷理科数学试题（含解析）‎ 注意事项：‎ ‎1．答题前填写好自己的姓名、班级、考号等信息 ‎2．请将答案正确填写在答题卡上 第I卷（选择题）‎ 请点击修改第I卷的文字说明 评卷人 得分 一、选择题（题型注释）‎ ‎1．设复数，在复平面内的对应点关于虚轴对称，，则（ ）‎ A.- 5 B.5 C.- 4+ i D.- 4 - i ‎2．设向量a,b满足|a+b|=，|a-b|=，则ab = ( )‎ A.1 B.2 C.3 D.5‎ ‎3．钝角三角形ABC的面积是，AB=1，BC= ，则AC=( )‎ A.5 B. C.2 D.1‎ ‎4．某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（ ）‎ A.0.8 B.0.75 C.0.6 D.0.45‎ ‎5．如图，网格纸上正方形小格的边长为1（表示1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（ ）‎ A. B. C. D.‎ ‎6．执行右图程序框图，如果输入的x,t均为2，则输出的S= （ ）‎ ‎ A.4 B.5 C.6 D.7 ‎ ‎7．设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x，则a= （ ）‎ A.0 B.1 C.2 D.3 ‎ ‎8．设F为抛物线C:的焦点，过F且倾斜角为30°的直线交C于A,B两点，O为坐标原点，则 ‎△OAB的面积为（ ）‎ A. B. C. D.‎ ‎9．直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，‎ 则BM与AN所成的角的余弦值为（ ）‎ A. B. C. D.‎ ‎10．设函数.若存在的极值点满足，则m的取值范围是（ ）‎ A. B.‎ C. D.‎ 第II卷（非选择题）‎ 请点击修改第II卷的文字说明 评卷人 得分 二、填空题（题型注释）‎ ‎11．的展开式中，的系数为15，则a=________.(用数字填写答案)‎ ‎12． 函数的最大值为_________.‎ ‎13．已知偶函数在单调递减，.若，则的取值范围是__________.‎ ‎14．设点M（,1），若在圆O:上存在点N，使得∠OMN=45°，则的取值范围是________.‎ 评卷人 得分 三、解答题（题型注释）‎ ‎15．已知数列满足=1，.‎ ‎（1）证明是等比数列，并求的通项公式；‎ ‎（2）证明：.‎ ‎16．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点.‎ ‎（1）证明：PB∥平面AEC；‎ ‎（2）设二面角D-AE-C为60°，AP=1，AD=，求三棱锥E-ACD的体积.‎ ‎17．某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：‎ 年份 ‎2007‎ ‎2008‎ ‎2009‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均纯收入y ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎（1）求y关于t的线性回归方程；‎ ‎（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.‎ 附：回归直线的斜率和截距的最小二乘法估计公式分别为：‎ ‎，‎ ‎18．设,分别是椭圆的左右焦点，M是C上一点且与x轴垂直，直线与C的另一个交点为N.‎ ‎（1）若直线MN的斜率为，求C的离心率；‎ ‎（2）若直线MN在y轴上的截距为2，且，求a,b.‎ ‎19．已知函数=.‎ ‎（1）讨论的单调性；‎ ‎（2）设，当时，,求的最大值；‎ ‎（3）已知，估计ln2的近似值（精确到0.001）‎ ‎20．如图，P是O外一点，PA是切线，A为切点，割线PBC与O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交O于点E。‎ 证明：（1）BE=EC；‎ ‎（2）ADDE=2‎ ‎21．在直角坐标系xoy中，以坐标原点为极点，x轴为极轴建立极坐标系，半圆C的极坐标方程为 ‎，‎ ‎.‎ ‎（1）求C的参数方程；‎ ‎（2）设点D在C上，C在D处的切线与直线垂直，根据（1）中你得到的参数方程，确定D的坐标.‎ ‎22．设函数=‎ ‎（1）证明：2；‎ ‎（2）若，求的取值范围.‎ 参考答案 ‎1．A ‎【解析】由题意知：，所以-5，故选A。‎ 考点：本小题主要考查复数的乘法，复数的几何意义，复数是高考的重点，年年必考，常常以选择或填空题的形式出现，难度不大，熟练基础知识是关键。‎ ‎2．A ‎【解析】因为=10，，两式相加得：，所以，故选A.‎ 考点：本小题主要考查平面向量的模、平面向量的数量积等平面向量知识，熟练基础知识与基本题型是解答好本类题目的关键。‎ ‎3．B ‎【解析】由面积公式得：，解得，所以或，当时，‎ 由余弦定理得：=1，所以，又因为AB=1，BC=，所以此时为等腰直角三角形，不合题意，舍去；所以，由余弦定理得：=5，所以，故选B.‎ 考点：本小题主要考查余弦定理及三角形的面积公式，考查解三角形的基础知识.‎ ‎4．A ‎【解析】设A=“某一天的空气质量为优良”，B=“随后一天的空气质量为优良”，则，故选A.‎ 考点：本小题主要考查条件概率的求法，熟练概率的基础知识是解答好本类题目的关键.‎ ‎5．C ‎【解析】因为加工前的零件半径为3，高为6，所以体积，又因为加工后的零件，左半部为小圆柱，半径为2，高4，右半部为大圆柱，半径为3，高为2，所以体积，所以削掉部分的体积与原体积之比为，故选C.‎ 考点：本小题主要考查立体几何中的三视图，考查同学们的空间想象能力.‎ ‎6．D ‎【解析】由题意知：当时，，；当时，，；当时，输出S=7，故选D。‎ 考点：本小题主要考查程序框图的基础知识，程序框图是新课标新增内容，是高考的重点，年年必考，主要以客观题的形式出现，经常也数列、不等式、函数等知识相结合，在知识的交汇处出题，应熟练这部分的基础知识.‎ ‎7．B ‎【解析】画出不等式组表示的平面区域,可知区域为三角形，平移直线，可知当经过两条直线 与的交点A（5，2）时，取得最大值8，故选B.‎ 考点：本小题主要考查在约束条件下的简单的目标函数的最值问题，正确画图与平移直线是解答这类问题的关键.‎ ‎8．D ‎【解析】由题意可知：直线AB的方程为，代入抛物线的方程可得：，设A、B，则所求三角形的面积为=，故选D.‎ 考点：本小题主要考查直线与抛物线的位置关系，考查两点间距离公式等基础知识，考查同学们分析问题与解决问题的能力.‎ ‎9．C ‎【解析】以C为原点，直线CA为x轴，直线CB为y轴，直线为轴，则设CA=CB=1，则 ‎，，A（1，0，0），，故，，所以，故选C.‎ 考点：本小题主要考查利用空间向量求线线角，考查空间向量的基本运算，考查空间想象能力等数学基本能力，考查分析问题与解决问题的能力.‎ ‎10．C ‎【解析】由题意知：的极值为，所以，因为，‎ 所以，所以即，所以，即 ‎3，而已知，所以3，故，解得或，故选C.‎ 考点：本小题主要考查利用导数研究的极值，考查三角函数，考查一元二次不等式的解法，考查分析问题与解决问题的能力.‎ ‎11．‎ ‎【解析】因为，所以令，解得，所以=15，解得.‎ 考点：本小题主要考查二项式定理的通项公式，求特定项的系数，题目难度不大，属于中低档.‎ ‎12．1‎ ‎【解析】由题意知：=‎ ‎==‎ ‎==，即，因为，所以的最大值为1.‎ 考点：本小题主要考查两角和与差的三角函数、三角函数的最值的求解，熟练公式是解答好本类题目的关键.‎ ‎13．‎ ‎【解析】因为是偶函数，所以不等式，又因为在上单调递减，所以，解得.‎ 考点：本小题主要考查抽象函数的奇偶性与单调性，考查绝对值不等式的解法，熟练基础知识是关键.‎ ‎14．‎ ‎【解析】由题意知：直线MN与圆O有公共点即可，即圆心O到直线MN的距离小于等于1即可，如图，‎ 过OA⊥MN，垂足为A，在中，因为∠OMN=45，所以=‎ ‎，‎ 解得，因为点M（,1），所以，解得，故的取值范围是 ‎.‎ 考点：本小题主要考查考查直线与圆的位置关系，考查数形结合能力和逻辑思维能力，考查同学们分析问题和解决问题的能力，有一定的区分度.‎ ‎15．‎ ‎【解析】试题分析：本题第（1）问，证明等比数列，可利用等比数列的定义来证明，之后利用等比数列，求出其通项公式；对第（2）问，可先由第（1）问求出，然后转化为等比数列求和，放缩法证明不等式.‎ 试题解析：（1）证明：由得，所以，所以是等比数列，首项为，公比为3，所以，解得.‎ ‎（2）由（1）知：，所以，‎ 因为当时，，所以，于是=，‎ 所以.‎ ‎【易错点】对第（1）问，构造数列证明等比数列不熟练；对第（2）问，想不到当时，，而找不到思路，容易想到用数学归纳法证明而走弯路.‎ 考点：本小题考查等比数列的定义、数列通项公式的求解、数列中不等式的证明等基础知识，考查同学们的逻辑推理能力，考查分析问题与解决问题的能力.数列是高考的热点问题之一，熟练数列的基础知识是解决好该类问题的关键.‎ ‎16．‎ ‎【解析】试题分析：本题第（1）问，证明直线与平面平行，可利用线面平行的判定定理来证明；对第（2）问，可先建立空间直角坐标系，由空间向量的坐标运算计算二面角，从而计算出AB，然后由棱锥的体积公式求出三棱锥的体积.‎ 试题解析：（1）证明：设O为AC与BD交点，连结OE，则由矩形ABCD知：O为BD的中点，因为E是BD的中点，所以OE∥PB，因为OE面AEC，PB面AEC，所以PB∥平面AEC。‎ ‎（2）以A为原点，直线AB、AD、AP分别为x、y、z轴建立空间直角坐标系，设AB=m，则 是平面AED的一个法向量，设是平面AEC的法向量，则 ‎，解得，，所以令，得，所以 ‎=，因为二面角的大小与其两个半平面的两个法向量的夹角相等哉互补，所以=，解得，因为E是PD的中点，所以三棱锥E-ACD的高为，所以三棱锥E-ACD的体积为==.‎ ‎【易错点】对第（1）问，证明线面平行时,容易漏掉条件；对第（2）问，二面角的大小与两个法向量夹角相等或互补的关系，一部分同学容易得出它们相等；并且计算法向量可能出现错误.‎ 考点：本小题考查空间中直线与平面平行等位置关系的证明、二面角的求解，空间几何体的体积的求法，考查利用空间向量知识解决立体几何的能力，考查同学们的逻辑推理能力、空间想象能力，考查分析问题以及解决问题的能力.‎ ‎17．（1）；（2）在2007至2013年该地区农村居民家庭人均纯收入在逐年增加，平均每年增加千元；元.‎ ‎【解析】试题分析：本题第（1）问，由给出的与公式求出与，从而求出回归直线方程；对第（2）问，由第（1）问求出的回归直线方程进行预测，令，可得的近似值.‎ 试题解析：（1）由题意知，，，所以 ‎=，‎ 所以==，所以线性回归方程为。‎ ‎（2）由（1）中的线性回归方程可知，，所以在2007至2013年该地区农村居民家庭人均纯收入在逐年增加，平均每年增加千元.‎ 令得：，故预测该地区在2015年农村居民家庭人均纯收入为元。‎ ‎【易错点】本题的易错点是第（1）问计算错误，第（2）问在2007至2013年该地区农村居民家庭人均纯收入的变化情况，不知道如何回答.‎ 考点：本小题主要考查线性回归方程的解法等基础知识，属中档题目，考查同学们分析问题与解决问题的能力.‎ ‎18．（1）；（2），.‎ ‎【解析】试题分析：本题第（1）问，可结合与x轴垂直，由勾股定理及椭圆定义求出椭圆的离心率；对第（2）问，观察到是三角形的中位线，然后结合向量的坐标运算及椭圆方程，可求出a,b.‎ 试题解析：（1）由题意知，，所以，由勾股定理可得：，由椭圆定义可得：=，解得C的离心率为。‎ ‎（2）由题意，原点O为的中点，∥y轴，所以直线与y轴的交点D（0，2）是线段的中点，故，即，由得，设，由题意知，则 ‎，即，代入C的方程得，将及代入得：，解得，.‎ ‎【易错点】对第（1）问，较容易，大部分同学都能计算出；对第（2）问,一部分同学考虑不到中位线，‎ 容易联立方程组求解而走弯路，并且容易出现计算失误.‎ 考点：本小题考查椭圆的几何意义（离心率的求解）、椭圆的方程、直线与椭圆的位置关系，考查数学中的待定系数法、设而不求思想 ‎ ，考查同学们的计算能力以及分析问题、解决问题的能力.圆锥曲线是高考的热点问题,年年必考,熟练本部分的基础知识是解答好本类问题的关键.‎ ‎19．（1）函数在R上是增函数；（2）2；（3）‎ ‎【解析】试题分析：本题第（1）问，判断函数的单调，关键是判断导数的正数；对第（2）问，可构造函数，对（3）问，可根据的取值讨论.‎ 试题解析：（1）因为，当且仅当时等号成立，所以函数在R上是增函数；‎ ‎（2）因为=，‎ 所以=.‎ ‎(1)当时, ,等号仅当时成立，所以在R上单调递增，而，所以对任意，；‎ ‎（2）当时，若满足，即时，，而，‎ 因此当时，，‎ 综上，的最大值为2.‎ ‎（3）由（2）知，，‎ 当时，，；‎ 当时，，，‎ ‎，所以的近似值为.‎ ‎【易错点】对第(Ι)问,函数单调性的判断，容易;对第（2）问,考虑不到针对去讨论；对第（3）问,‎ 找不到思路.‎ 考点：本小题主要考查利用导数研究函数的单调性、极值、最值等知识，综合性较强，考查函数与方程、分类讨论等数学思想方法，考查同学们分析问题、解决问题的能力，熟练函数与导数的基础知识以及基本题型是解答好本类题目的关键.‎ ‎20．（1）见解析 （2）见解析 ‎【解析】试题分析：本题第（1）问，先由已知得出PA=PD，然后由对应角相等，拆分角得出结论；对第（2）问，可由切割线定理得出，，‎ 然后由相交弦定理，得出结论.‎ 试题解析：（1）连结AB，AC，由题意知PA=PD，故，因为，‎ ‎，，所以，从而，因此BE=EC.‎ ‎（2）由切割线定理得：，因为，所以，，‎ 由相交弦定理得：==‎ ‎=，所以等式成立.‎ ‎【易错点】对第（1）问，不容易找到思路;第（2）问中不会灵活应用已知条件而出错.‎ 考点：本小题主要考查圆的切线、割线、相交弦定理、圆内接四边形等平面几何知识，考查数形结合思想，考查分析问题、解决问题的能力.‎ ‎21．（1）是参数，；（2）‎ ‎【解析】试题分析：本题第（1）问，由极坐标与普通方程的互化关系可得出C的普通方程为：，从而写出C的参数方程为是参数，.；对第（2）问，可先设D点坐标为，然后由C在点D处的切线与垂直，得出，从而得出，写出D点坐标.‎ 试题解析：（1）设点M是C上任意一点，则由可得C的普通方程为：，‎ 即，‎ 所以C的参数方程为是参数，.‎ ‎（2）设D点坐标为，由（1）知C是以G（1，0）为圆心，1为半径的上半圆，‎ 因为C在点D处的切线与垂直，所以直线GD与的斜率相同，，，‎ 故D点的直角坐标为，即.‎ ‎【易错点】对第（1）问，极坐标与普通方程、参数方程之间的互化,有一部分学生不熟练而出错;对第(2)问,不理解题意而出错.‎ 考点：本小题主要考查坐标系与参数方程的基础知识,熟练这部分的基础知识是解答好本类题目的关键.‎ ‎22．（2）‎ ‎【解析】试题分析：本题第（1）问，可由绝对值不等式的几何意义得出，从而得出结论；对第（2）问，由去掉一个绝对值号，然后去掉另一个绝对值号，解出的取值范围.‎ 试题解析：（1）证明：由绝对值不等式的几何意义可知：，当且仅当时，取等号，所以.‎ ‎（2）因为，所以 ‎ ‎，解得：.‎ ‎【易错点】在应用均值不等式时,注意等号成立的条件:一正二定三相等.‎ 考点：本小题主要考查不等式的证明、绝对值不等式的几何意义、绝对值不等式的解法、求参数范围等不等式知识，熟练基础知识是解答好本类题目的关键.‎