- 2021-05-13 发布 |
- 37.5 KB |
- 11页


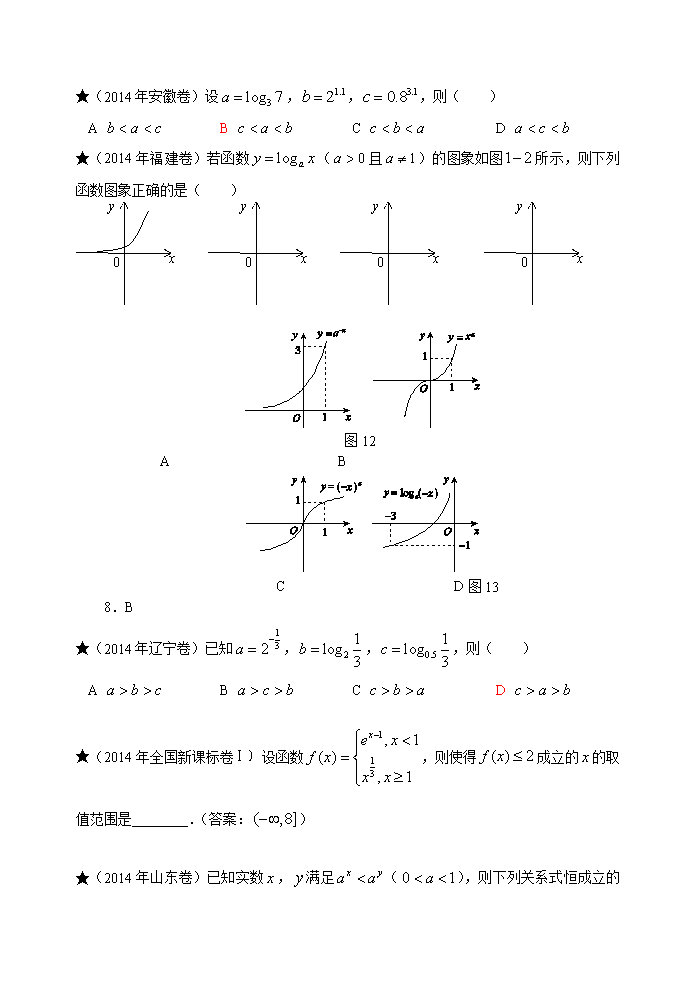
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学文真题分类汇编2函数与导数
2014年全国高考数学试题汇编二(函数与导数) ★(2014年安徽卷)若函数是周期为4的奇函数,且在上的解析式为,则 .(答案:) ★(2014年北京卷)下列函数中,定义域是且为增函数的是( ) A B C D ★(2014年山东卷)函数的定义域为( ) A B C D ★(2014年湖南卷)下列函数中,既是偶函数又在区间上单调递增的是( ) A B C D ★(2014年江苏卷)已知函数,其中是自然对数的底数. (1)证明:是上的偶函数; (2)若关于的不等式在上恒成立,求实数的取值范围; (3)已知正数满足:存在,使得成立.试比较与的大小,并证明你的结论. ★(2014年四川卷)已知函数,其中,,为自然对数的底数. (1)设是函数的导函数,求函数在区间上的最小值; (2)若,函数在区间内有零点,证明:. ★(2014年重庆卷)下列函数为偶函数的是( ) A B C D ★(2014年广东卷)下列函数为奇函数的是( ) A B C D ★(2014年湖北卷)已知是定义在R上的奇函数,当时,,则函数的零点的集合为( ) A B C D ★(2014年湖南卷)若是偶函数,则 .(答案:) ★(2014年全国卷)奇函数的定义域为R.若为偶函数,且,则( ) A B C D ★(2014年新课标全国卷Ⅱ)偶函数的图像关于直线对称,,则 .(答案:) ★(2014年全国新课标卷Ⅰ)设函数,的定义域都为R,且是奇函数,是偶函数,则下列结论中正确的是( ) A 是偶函数 B 是奇函数 C 是奇函数 D 是奇函数 ★(2014年四川卷)设是定义在R上的周期为2的函数,当时, ,则 .(答案:1) ★(2014年江苏卷)已知函数,若对于任意,都有成立,则实数的取值范围是 .(答案:) ★(2014年全国卷)函数的最大值为________.(答案:) ★(2014年安徽卷)设,,,则( ) A B C D y x 0 y x 0 y x 0 y x 0 ★(2014年福建卷)若函数(且)的图象如图所示,则下列函数图象正确的是( ) 图12 A B C D图13 8.B ★(2014年辽宁卷)已知,,,则( ) A B C D ★(2014年全国新课标卷Ⅰ)设函数,则使得成立的的取值范围是________.(答案:) ★(2014年山东卷)已知实数,满足() ,则下列关系式恒成立的是( ) A B C D ★(2014年陕西卷)下列函数中,满足“”的单调递增函数是( ) A B C D ★(2014年陕西卷)已知,,则________.(答案:) ★(2014年四川卷)已知,,,,则下列等式一定成立的是( ) A B C D ★(2014年四川卷)设,过定点的动直线和过定点的动直线交于点,则的取值范围是( ) A B C D ★(2014年天津卷)设,,,则( ) A B C D ★(2014年天津卷)函数的单调递减区间是________.(答案:) ★(2014年安徽卷)________.(答案:) 29、[2014·浙江卷] 在同一直角坐标系中,函数f(x)=xa(x>0),g(x)=logax的图像可能是( ) A B C D 图12 8.D y x 0 ★(2014年广东卷)已知等比数列的各项均为正数,且,则________.(答案:5) ★(2014年山东卷)已知函数(,为常数, 其中,且)的图象如图所示,则下列结论成立的是( ) A , B , C , D , ★(2014年重庆卷)若,则的最小值是( ) A B C D ★(2014年湖北卷)如图所示,函数的图像由两条射线和三条线段组成. 若,,则正实数的取值范围为________.(答案:) ★(2014年江苏卷)已知是定义在上且周期为3的函数,当时,.若函数在区间上有个零点(互不相同),则实数的取值范围是________.(答案:) B9 函数与方程 ★(2014年北京卷)已知函数,在下列区间中,包含的零点的区间是( ) A B C D ★(2014年浙江卷)若函数,且,则( ) A B C D ★(2014年重庆卷)已知函数且在内有且仅有两个不同的零点,则实数的取值范围是( ) A B C D ★(2014年福建卷)函数的零点个数是_____.(答案:2) ★(2014年江西卷)已知函数.若,则( ) A B C 1 D 2 ★(2014年浙江卷)设函数,若,则_____.(答案:) 41、(2014年浙江卷)函数(). (1)讨论的单调性; (2)若在区间是增函数,求的取值范围. ★(2014年天津卷)已知函数,若函数恰有4个零点,则实数的取值范围为_____.(答案:) 3 4 5 0.5 0.7 0.8 0 t p ★(2014年北京卷)加工爆米花时,爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”.在特定条件下,可食用率与加工时间(单位: 分钟)满足函数关系(,,是常数), 如图记录了三次实验的数据.根据上述函数模型和实验数据, 可以得到最佳加工时间为( ) A 3.50分钟 B 3.75分钟 C 4.00分钟 D 4.25分钟 ★(2014年陕西卷)如图所示,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切).已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( ) A B C D ★(2014年陕西卷)设函数,. (1)当(为自然对数的底数)时,求的极小值; (2)讨论函数零点的个数; (3)若对任意,恒成立,求的取值范围. ★(2014年安徽卷)设函数,其中. (1)讨论在其定义域上的单调性; (2)当时,求取得最大值和最小值时的的值. ★(2014年北京卷)已知函数. (1)求在区间上的最大值; (2)若过点存在3条直线与曲线相切,求的取值范围; (3)问过点,,分别存在几条直线与曲线相切?(只需写出结论) ★(2014年福建卷)已知函数(为常数)的图像与轴交于点,曲线在点处的切线斜率为. (1)求的值及函数的极值; (2)证明:当时,; (3)证明:对任意给定的正数,总存在,使得当时,恒有. ★(2014年广东卷)曲线在点处的切线方程为________.(答案:) ★(2014年江苏卷)在平面直角坐标系中,若曲线(,为常数)过点,且该曲线在点处的切线与直线平行,则的值是________.(答案:) ★(2014年全国新课标卷Ⅰ)设函数(),曲线在点处的切线斜率为0. (1)求; (2)若存在,使得,求的取值范围. ★(2014年山东卷)设函数,其中为常数. (1)若,求曲线在点处的切线方程; (2)讨论函数的单调性. ★(2014年四川卷)设等差数列的公差为,点在函数的图象上(). (1)证明:数列为等比数列; (2)若,函数的图像在点处的切线在轴上的截距为,求数列的前项和. ★(2014年天津卷)已知函数(). (1)求的单调区间和极值; (2)若对于任意的,都存在,使得,求的取值范围. ★(2014年四川卷)已知函数,其中,,为自然对数的底数. (1)设是函数的导函数,求函数在区间上的最小值; (2)若,函数在区间内有零点,证明:. ★(2014年安徽卷)设函数f(x)=1+(1+a)x-x2-x3,其中a>0. (1)讨论f(x)在其定义域上的单调性; (2)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值. 20.、[2014·北京卷] 已知函数f(x)=2x3-3x. (1)求f(x)在区间[-2,1]上的最大值; (2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围; (3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论) 22.、[2014·福建卷] 已知函数f(x)=ex-ax(a为常数)的图像与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1. (1)求a的值及函数f(x)的极值; (2)证明:当x>0时,x2<ex; (3)证明:对任意给定的正数c,总存在x0,使得当x∈(x0,+∞)时,恒有x<cex. 21.[2014·广东卷] 已知函数f(x)=x3+x2+ax+1(a∈R). (1)求函数f(x)的单调区间; (2)当a<0时,试讨论是否存在x0∈∪,使得f(x0)=f. 21.、[2014·湖南卷] 已知函数f(x)=xcos x-sin x+1(x>0). (1)求f(x)的单调区间; (2)记xi为f(x)的从小到大的第i(i∈N*)个零点,证明:对一切n∈N*,有++…+<. 11.[2014·江西卷] 若曲线y=xln x上点P处的切线平行于直线2x-y+1=0,则点P的坐标是________. 12.、[2014·辽宁卷] 当x∈[-2,1]时,不等式ax3-x2+4x+3≥0恒成立,则实数a的取值范围是( ) A.[-5,-3] B. C.[-6,-2] D.[-4,-3] 12.C 11.[2014·新课标全国卷Ⅱ] 若函数f(x)=kx-ln x在区间(1,+∞)单调递增,则k的取值范围是( ) A.(-∞,-2] B.(-∞,-1] C.[2,+∞) D.[1,+∞) 11.D 21.[2014·新课标全国卷Ⅱ] 已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2. (1)求a; (2)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点. 12.[2014·全国新课标卷Ⅰ] 已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( ) A.(2,+∞) B.(1,+∞) C.(-∞,-2) D.(-∞,-1) 12.C 20.,[2014·山东卷] 设函数f(x)=aln x+,其中a为常数. (1)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程; (2)讨论函数f(x)的单调性. 21.[2014·浙江卷] 已知函数f(x)=x3+3|x-a|(a>0).若f(x)在[-1,1]上的最小值记为g(a). (1)求g(a); (2)证明:当x∈[-1,1]时,恒有f(x)≤g(a)+4. 19.[2014·重庆卷] 已知函数f(x)=+-ln x-,其中a∈R,且曲线y=f(x)在点(1,f(1))处的切线垂直于直线y=x. (1)求a的值; (2)求函数f(x)的单调区间与极值. 10.[2014·江西卷] 在同一直角坐标系中,函数y=ax2-x+与y=a2x3-2ax2+x+a(a∈R)的图像不可能是( ) A B C D 10.B 查看更多