高中数学概念总结高考必看之经典2
高中數學概念總結
一、 函數
1、 若集合A中有n個元素,則集合A的所有不同的子集個數為,所有非空真子集的個數是。
二次函數的圖像的對稱軸方程是,頂點座標是。用待定係數法求二次函數的解析式時,解析式的設法有三種形式,即,和 (頂點式)。
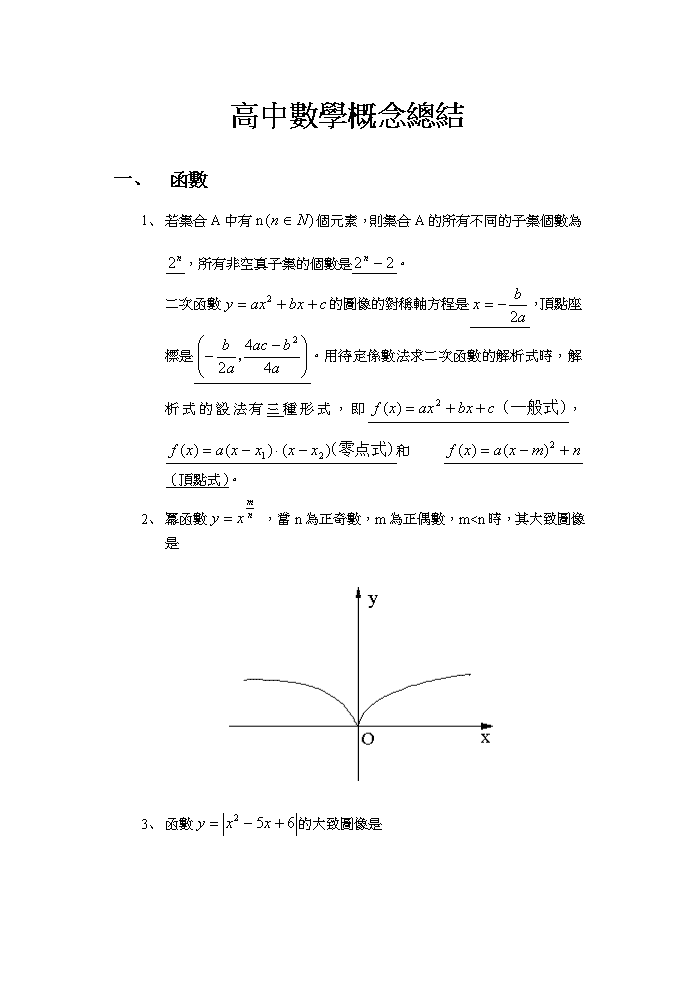
2、 冪函數 ,當n為正奇數,m為正偶數,m
0,=0,<0,等價於直線與圓相交、相切、相離;
②考查圓心到直線的距離與半徑的大小關係:距離大於半徑、等於半徑、小於半徑,等價於直線與圓相離、相切、相交。
15、抛物線標準方程的四種形式是:
16、抛物線的焦點座標是:,准線方程是:。
若點是抛物線上一點,則該點到抛物線的焦點的距離(稱為焦半徑)是:,過該抛物線的焦點且垂直於抛物線對稱軸的弦(稱為通徑)的長是:。
17、橢圓標準方程的兩種形式是:和
。
18、橢圓的焦點座標是,准線方程是,離心率是,通徑的長是。其中。
19、若點是橢圓上一點,是其左、右焦點,則點P的焦半徑的長是和
。
20、雙曲線標準方程的兩種形式是:和
。
21、雙曲線的焦點座標是,准線方程是,離心率是,通徑的長是,漸近線方程是。其中。
22、與雙曲線共漸近線的雙曲線系方程是。與雙曲線共焦點的雙曲線系方程是。
23、若直線與圓錐曲線交於兩點A(x1,y1),B(x2,y2),則弦長為 ;
若直線與圓錐曲線交於兩點A(x1,y1),B(x2,y2),則弦長為 。
24、圓錐曲線的焦參數p的幾何意義是焦點到准線的距離,對於橢圓和雙曲線都有:。
25、平移坐標軸,使新坐標系的原點在原坐標系下的座標是(h,k
),若點P在原坐標系下的座標是在新坐標系下的座標是,則=,=。
一、 極座標、參數方程
1、 經過點的直線參數方程的一般形式是:。
2、 若直線經過點,則直線參數方程的標準形式是:。其中點P對應的參數t的幾何意義是:有向線段的數量。
若點P1、P2、P是直線上的點,它們在上述參數方程中對應的參數分別是則:;當點P分有向線段時,;當點P是線段P1P2的中點時,。
3、圓心在點,半徑為的圓的參數方程是:。
3、 若以直角坐標系的原點為極點,x軸正半軸為極軸建立極坐標系,點P的極座標為直角坐標為,則,,。
1、 經過極點,傾斜角為的直線的極座標方程是:,
經過點,且垂直於極軸的直線的極座標方程是:,
經過點且平行於極軸的直線的極座標方程是:,
經過點且傾斜角為的直線的極座標方程是:。
2、 圓心在極點,半徑為r的圓的極座標方程是;
圓心在點的圓的極座標方程是;
圓心在點的圓的極座標方程是;
圓心在點,半徑為的圓的極座標方程是。
3、 若點M、N,則。
二、 立體幾何
1、求二面角的射影公式是,其中各個符號的含義是:是二面角的一個面內圖形F的面積,是圖形F在二面角的另一個面內的射影,是二面角的大小。
2、若直線在平面內的射影是直線,直線m是平面內經過的斜足的一條直線,與所成的角為,與m所成的角為, 與m所成的角為θ,則這三個角之間的關係是。
3、體積公式:
柱體:,圓柱體:。
斜棱柱體積:(其中,是直截面面積,是側棱長);
錐體:,圓錐體:。
台體:, 圓臺體:
球體:。
3、 側面積:
直棱柱側面積:,斜棱柱側面積:;
正棱錐側面積:,正棱臺側面積:;
圓柱側面積:,圓錐側面積:,
圓臺側面積:,球的表面積:。
5、幾個基本公式:
弧長公式:(是圓心角的弧度數,>0);
扇形面積公式:;
圓錐側面展開圖(扇形)的圓心角公式:;
圓臺側面展開圖(扇環)的圓心角公式:。
經過圓錐頂點的最大截面的面積為(圓錐的母線長為,軸截面頂角是θ):
十一、比例的幾個性質
1、比例基本性質:
2、反比定理:
3、更比定理:
3、 合比定理;
4、 分比定理:
5、 合分比定理:
6、 分合比定理:
7、 等比定理:若,,則。
十二、複合二次根式的化簡
當是一個完全平方數時,對形如的根式使用上述公式化簡比較方便。