2015高考数学人教A版本(10-5古典概型与几何概型)一轮复习学案
【走向高考】2015届高考数学一轮总复习 10-5古典概型与几何概型课后强化作业 新人教A版
基础巩固强化
一、选择题
1.已知α、β、γ是不重合平面,a、b是不重合的直线,下列说法正确的是( )
A.“若a∥b,a⊥α,则b⊥α”是随机事件
B.“若a∥b,a⊂α,则b∥α”是必然事件
C.“若α⊥γ,β⊥γ,则α⊥β”是必然事件
D.“若a⊥α,a∩b=P,则b⊥α”是不可能事件
[答案] D
[解析] ⇒b⊥α,故A错;⇒b∥α或b⊂α,故B错;当α⊥γ,β⊥γ时,α与β可能平行,也可能相交(包括垂直),故C错;如果两条直线垂直于同一个平面,则此二直线必平行,故D为真命题.
2.(文)4张卡片上分别写有数字1、2、3、4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
A. B.
C. D.
[答案] C
[解析] 取出两张卡片的基本事件构成集合Ω={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}共6个基本事件.
其中数字之和为奇数包含(1,2),(1,4),(2,3),(3,4)共4个基本事件,
∴所求概率为P==.
(理)(2013·宿州质检)一颗质地均匀的正方体骰子,其六个面上的点数分别为1、2、3、4、5、6,将这颗骰子连续抛掷三次,观察向上的点数,则三次点数依次构成等差数列的概率为( )
A. B.
C. D.
[答案] A
[解析] 连续抛掷三次共有63=216(种)情况,记三次点数分别为a、b、c,则a+c=2b,所以a+c为偶数,则a、c的奇偶性相同,且a、c允许重复,一旦a、c确定,b
也唯一确定,故a,c共有2×32=18(种),所以所求概率为=,故选A.
3.(文)(2013·惠州调研)一个袋中装有2个红球和2个白球,现从袋中取出1个球,然后放回袋中再取出1个球,则取出的2个球同色的概率为( )
A. B.
C. D.
[答案] A
[解析] P==.
(理)(2013·皖南八校联考)一个袋子中有5个大小相同的球,其中有3个黑球与2个红球,如果从中任取两个球,则恰好取到两个同色球的概率是( )
A. B.
C. D.
[答案] C
[解析] P==.
4.(文)(2013·郑州第一次质量预测)一数学兴趣小组利用几何概型的相关知识做实验计算圆周率,他们向一个边长为1米的正方形区域均匀撒豆,测得正方形区域有豆5120颗,正方形的内切圆区域有豆4009颗,则他们所测得的圆周率为(保留三位有效数字)( )
A.3.13 B.3.14
C.3.15 D.3.16
[答案] A
[解析] 根据几何概型的定义有=,得π≈3.13.
(理)点P在边长为1的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )
A. B.
C. D.π
[答案] C
[解析] 由题意可知,当动点P位于扇形ABD内时,动点P到定点A的距离|PA|<1,根据几何概型可知,动点P到定点A的距离|PA|<1的概率为=,故选C.
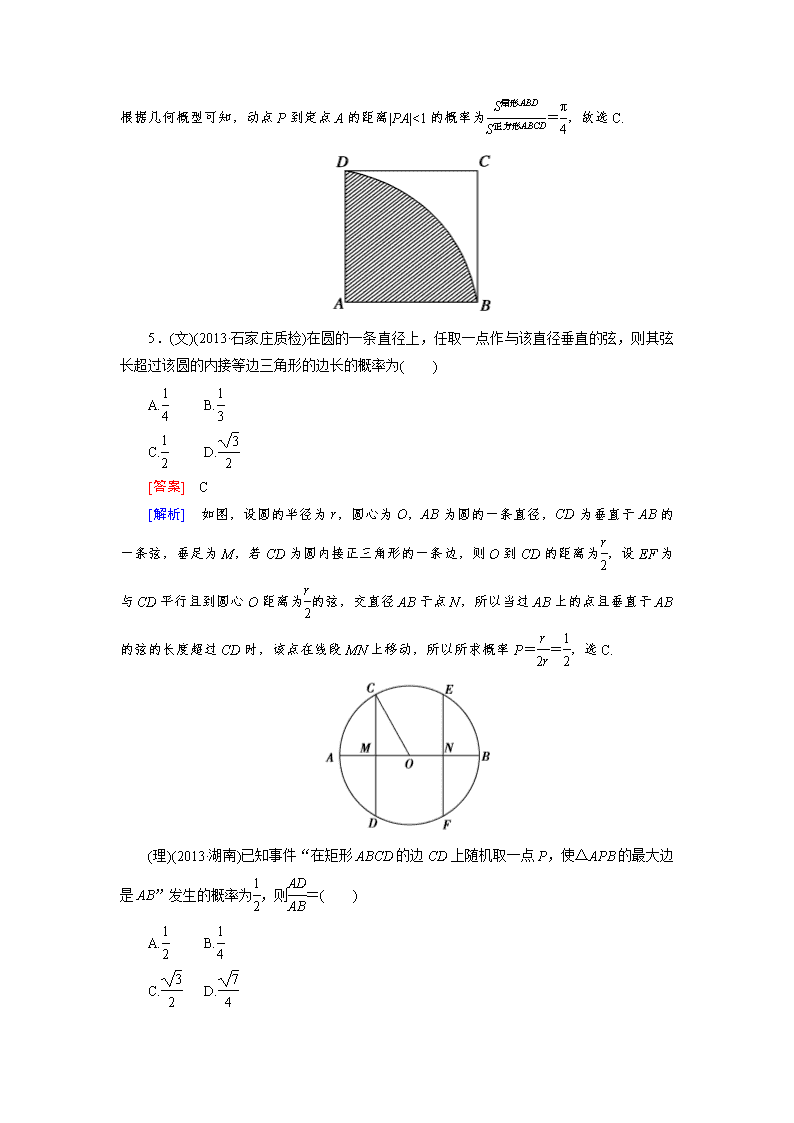
5.(文)(2013·石家庄质检)在圆的一条直径上,任取一点作与该直径垂直的弦,则其弦长超过该圆的内接等边三角形的边长的概率为( )
A. B.
C. D.
[答案] C
[解析] 如图,设圆的半径为r,圆心为O,AB为圆的一条直径,CD为垂直于AB的一条弦,垂足为M,若CD为圆内接正三角形的一条边,则O到CD的距离为,设EF为与CD平行且到圆心O距离为的弦,交直径AB于点N,所以当过AB上的点且垂直于AB的弦的长度超过CD时,该点在线段MN上移动,所以所求概率P==,选C.
(理)(2013·湖南)已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为,则=( )
A. B.
C. D.
[答案] D
[解析]
由题意知AB>AD,如图,当点P与E(或F)重合时,△ABP中,AB=BP(或AP),当点P在EF上运动时,总有AB>AP,AB>BP,由题中事件发生的概率为知,点P的分界点E、F恰好是边CD的四等分点,由勾股定理可得AB2=AF2=(AB)2+AD2,解得()2=,即=,故选D.
6.(2013·武昌区联考)若从区间(0,2)内随机取两个数,则这两个数的比不小于4的概率为( )
A. B.
C. D.
[答案] C
[解析] 设这两个数分别为x,y,则由条件知0
n的概率与mn的概率为×=,
∴满足m≥n的概率为P=+=.
8.(文)(2012·浙江文,12)从边长为1的正方形的中心和顶点这五个点中,随机(等可能)取两点,则该两点间的距离为的概率是________.
[答案]
[解析]
由五个点中随机取两点共有10种取法.由图可知两点间的距离为的是中心和四个顶点组成的4条线段,故概率为P==.
(理)在区间[1,5]和[2,4]分别各取一个数,记为m和n,则方程+=1表示焦点在x轴上的椭圆的概率是________.
[答案]
[解析] ∵方程+=1表示焦点在x轴上的椭圆,∴m>n.
由题意知,在矩形ABCD内任取一点P(m,n),求P点落在阴影部分的概率,易知直线m=n恰好将矩形平分,
∴p=.
9.(文)在区间[-1,1]上随机取一个数k,则直线y=k(x+2)与圆x2+y2=1有公共点的概率为________.
[答案]
[解析] ∵直线与圆有公共点,∴≤1,
∴-≤k≤.故所求概率为P==.
(理)(2013·大连、沈阳联考)若利用计算机在区间(0,1)上产生两个不等的随机数a和b,则方程x=2-有不等实数根的概率为________.
[答案]
[解析]
方程x=2-化为x2-2x+2b=0,
∵方程有两个不等实根,
∴Δ=8a-8b>0,∴a>b,
如图可知,所求概率P=.
三、解答题
10.(文)设平面向量am=(m,1),bn=(2,n),其中m、n∈{1,2,3,4}.
(1)请列出有序数组(m,n)的所有可能结果;
(2)记“使得am⊥(am-bn)成立的(m,n)”为事件A,求事件A发生的概率.
[解析] (1)有序数组(m,n)的所有可能结果为:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共16个.
(2)由am⊥(am-bn)得m2-2m+1-n=0,即n=(m-1)2
由于m、n∈{1,2,3,4},故事件A包含的基本事件为(2,1),(3,4),共2个.又基本事件的总数为16,故所求的概率为P(A)==.
(理)(2013·北京东城区统一检测)袋内装有6个球,这些球依次被编号为1、2、3、…、6,设编号为n的球重n2-6n+12(单位:g),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
[解析] (1)若编号为n的球的重量大于其编号,
则n2-6n+12>n,即n2-7n+12>0.
解得n<3,或n>4.
所以n=1,2,5,6.
所以从袋中任意取出一个球,其重量大于其编号的概率P==.
(2)不放回地任意取出2个球,这两个球编号的所有可能情形为(不分取出的先后次序):
1,2;1,3;1,4;1,5;1,6;
2,3;2,4;2,5;2,6;
3,4;3,5;3,6;
4,5;4,6;
5,6.
共有15种.
设编号分别为m与n(m,n∈{1,2,3,4,5,6},且m≠n)的球的重量相等,则有m2-6m+12=n2-6n+12,即有(m-n)(m+n-6)=0.
所以m=n(舍去),或m+n=6.
满足m+n=6的情形为:1,5;2,4,共2种.
故所求事件的概率为.
能力拓展提升
一、选择题
11.(2013·北京海淀期末)一对年轻夫妇和其两岁的孩子做游戏,让孩子把分别写有“1”“3”“1”“4”的四张卡片随机排成一行,若卡片按从左到右的顺序排成“1314”,则孩子会得到父母的奖励,那么孩子受到奖励的概率为( )
A. B.
C. D.
[答案] A
[解析] 先从4个位置中选一个排4,再从剩下位置中选一个排3,所有可能的排法有4×3=12种,满足要求的排法只有1种,∴所求概率为P=.
12.(文)(2012·辽宁文,11)在长为12cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC、CB的长,则该矩形面积大于20cm2的概率为( )
A. B.
C. D.
[答案] C
[解析] 在长为12cm的线段AB上任取一点C,设AC=x,则BC=12-x,∴x(12-x)>20,∴2x时,即只要点落到阴影部分,就表示张先生在离开家之前能拿到报纸,即所求事件A发生,所以P(A)==.
15.(2013·南京模拟)在集合A={2,3}中随机取一个元素m,在集合B={1,2,3}中随机取一个元素n,得到点P(m,n),则点P落在圆x2+y2=9内部的概率为________.
[答案]
[解析] 点P的取法有2×3=6种,
点P在圆内部,则m2+n2<9,
∴m=2,n=1或2.
∴所求概率P==.
三、解答题
16.(文)某饮料公司对一名员工进行测试以便确定考评级别,公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,测评为优秀;若3杯选对2杯测评为良好;否测评为合格.假设此人对A和B饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
[解析] 将5杯饮料编号为:1,2,3,4,5,编号1、2、3表示A饮料,编号4、5表示B饮料,则从5杯饮料中选出3杯的所有可能情况为:(123),(124),(125),(134),(135),(145),(234)(235),(245),(345),共有10种
令D表示此人被评为优秀的事件,E表示此人被评为良好的事件,F表示此人被评为良好及以上的事件,则
(1)P(D)=,
(2)P(E)=,P(F)=P(D)+P(E)=.
(理)袋子中放有大小和形状相同的小球若干个,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个.已知从袋子中随机抽取1个小球,取到标号是2的小球的概率是.
(1)求n的值;
(2)从袋子中不放回地随机抽取两个小球,记第一次取出的小球标号为a,第二次取出的小球标号为b.
①设事件A表示“a+b=2”,求事件A的概率;
②在区间[0,2]内任取两个实数x、y,求事件“x2+y2>(a-b)2恒成立”的概率.
[解析] (1)由题意可知:=,解得n=2.
(2)将标号为2的小球记作a1,a2
①两次不放回抽取小球的所有基本事件为:(0,1),(0,a1),(0,a2),(1,0),(1,a1),(1,a2),(a1,0),(a1,1),(a1,a2),(a2,0),(a2,1),(a2,a1),共12个,
事件A包含的基本事件为:(0,a1),(0,a2),(a1,0),(a2,0),共4个.
∴P(A)==.
②记“x2+y2>(a-b)2恒成立”为事件B,则事件B等价于“x2+y2>4”,(x,y)可以看成平面中的点,
则全部结果所构成的区域Ω={(x,y)|0≤x≤2,0≤y≤2,x,y∈R},而事件B所构成的区域B={(x,y)|x2+y2>4,x,y∈Ω},
∴P(B)===1-.
考纲要求
1.理解古典概型及其概率计算公式.
2.会计算一些随机事件所含的基本事件数及事件发生的概率.
3.了解随机数的意义,能运用模拟方法估计概率.
4.了解几何概型的意义.
补充说明
1.求解与角度有关的几何概型的注意点
当涉及射线的转动,扇形中有关落点区域问题时,应以角的大小作为区域度量来计算概率,切不可用线段代替,这是两种不同的度量手段.
2..求解古典概型概率,首先要找准基本事件,判断的标准就是有限性和等可能性.基本事件空间中基本事件的计算方法和事件A中包含的基本事件计算方法必须保持一致,计数时可以采取一一列举的方法,也可以采用模型化方法或用计数原理求,并辅以必要的文字说明.
3.注意事件是否互斥;遇到“至多”、“至少”等事件时,注意对立事件概率公式的应用.
备选习题
1.
(2013·哈尔滨二模)如图的矩形长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,由此我们可以估计出阴影部分的面积约为( )
A. B.
C. D.
[答案] C
[解析] 由几何概型的概率公式,得=,所以阴影部分面积约为,故选C.
2.从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( )
A. B.
C. D.
[答案] D
[解析] 如图正六边形ABCDEF,从6个顶点中随机选择4个顶点有ABCD,ABCE,ABCF,ABDE,ABDF,ACDE,ACDF,ACEF,ADEF,BCDE,BCDF,BCEF,ABEF,
BDEF,CDEF共15种选法,基本事件总数为15,其中四边形是矩形的有ABDE,BCEF,CDFA共3种,所以所求概率为P==.
3.先后抛掷两枚均匀的正方体骰子(他们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x、y,则log2xy=1的概率为( )
A. B.
C. D.
[答案] C
[解析] 先后抛掷两枚骰子,向上点数共有6×6=36种不同结果,其中满足log2xy=1,
即y=2x的情况如下:
x=1时,y=2;x=2时,y=4;x=3时,y=6,共3种.
∴所求概率为P==.
[点评] 注意细微差别,若把题目中的条件log2xy=1改为log2xy>1,则所求概率为( )
此时答案为A
这是因为抛掷两枚骰子共有62=36种不同结果,
∵log2xy>1,∴y>2x.
当x=1时,y有4种取法;当x=2时,y有2种取法;当x=3时,没有y满足,
∴满足y>2x的取法共有4+2=6种,
故所求概率P==.
若改为logx2y<1呢?
4.设a∈[0,2],b∈[0,4],则函数f(x)=x2+2ax+b在R上有两个不同零点的概率为________.
[答案]
[解析]
∵f(x)有两个不同零点,∴Δ=4a2-4b>0,∴b
查看更多