- 2021-05-13 发布 |
- 37.5 KB |
- 3页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考高中数学四种命题的相互关系
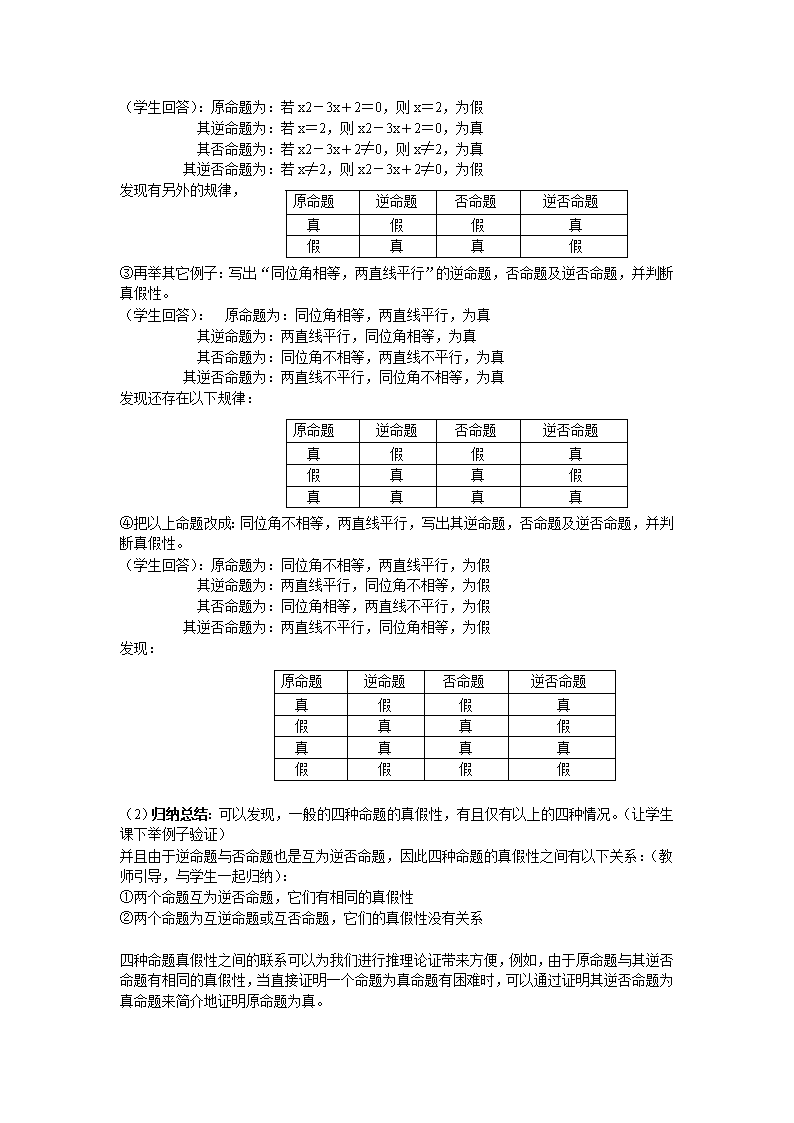
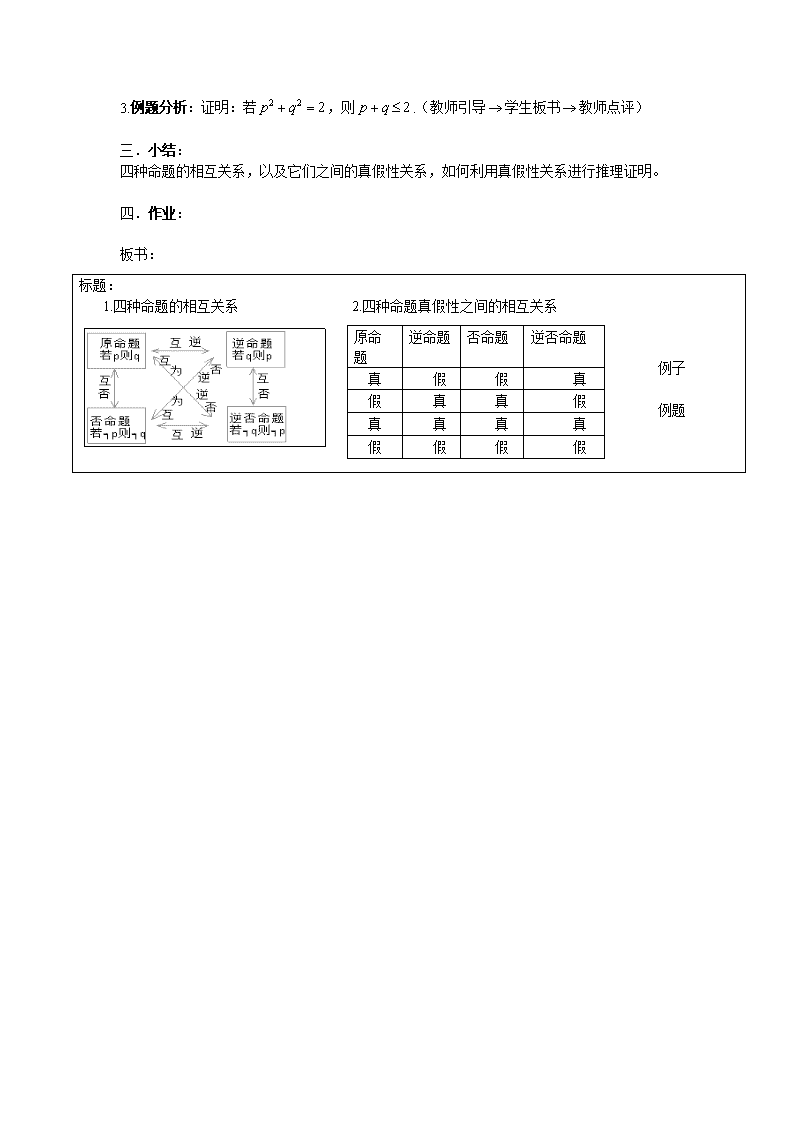
四种命题的相互关系 教学目标:1.熟练四种命题之间的关系,及四种命题的真假性之间的关系,并能利用四种命题真假性之间的内在联系进行推理论证 2.培养学生简单推理的思维能力. 教学重点:四种命题之间的相互关系即真假性之间的联系 教学难点:利用真假性之间的内在联系进行推理论证. 授课类型:新授课 教具准备:多媒体课件. 教学过程: 一. 复习引入: 1. 教学四种命题的概念: 原命题 逆命题 否命题 逆否命题 若,则 若,则 若,则 若,则 二.新课教授 1.四种命题间的相互关系 下列四个命题中, (1)若f (x) 是正弦函数,则f (x) 是周期函数; (2)若f (x) 是周期函数,则f (x) 是正弦函数; (3)若f (x) 不是正弦函数,则f (x) 不是周期函数; (4)若f (x) 不是周期函数,则f (x) 不是正弦函数; 命题(1)与命题(2)(3)(4)之间的关系我们已经了解,那么任意两个命题间的关系是: (老师引导—学生回答) 归纳:原命题、逆命题、否命题 和逆否命题之间的关系: 2.四种命题真假性之间的关系 (1)讨论: ①例1中三个命题的真假与它们的逆命题、否命题、逆否命题的真假间关系: (学生回答):原命题(1)为真 其逆命题(2)为假 其否命题(3)为假 其逆否命题(4)为真 发现有以下规律: 原命题 逆命题 否命题 逆否命题 真 假 假 真 ②(探究中)以“若x2-3x+2=0,则x=2”为原命题,写出其逆命题,否命题及逆否命题,并判断真假性。 (学生回答):原命题为:若x2-3x+2=0,则x=2,为假 其逆命题为:若x=2,则x2-3x+2=0,为真 其否命题为:若x2-3x+2≠0,则x≠2,为真 其逆否命题为:若x≠2,则x2-3x+2≠0,为假 原命题 逆命题 否命题 逆否命题 真 假 假 真 假 真 真 假 发现有另外的规律, ③再举其它例子:写出“同位角相等,两直线平行”的逆命题,否命题及逆否命题,并判断真假性。 (学生回答): 原命题为:同位角相等,两直线平行,为真 其逆命题为:两直线平行,同位角相等,为真 其否命题为:同位角不相等,两直线不平行,为真 其逆否命题为:两直线不平行,同位角不相等,为真 发现还存在以下规律: 原命题 逆命题 否命题 逆否命题 真 假 假 真 假 真 真 假 真 真 真 真 ④把以上命题改成:同位角不相等,两直线平行,写出其逆命题,否命题及逆否命题,并判断真假性。 (学生回答):原命题为:同位角不相等,两直线平行,为假 其逆命题为:两直线平行,同位角不相等,为假 其否命题为:同位角相等,两直线不平行,为假 其逆否命题为:两直线不平行,同位角相等,为假 原命题 逆命题 否命题 逆否命题 真 假 假 真 假 真 真 假 真 真 真 真 假 假 假 假 发现: (2)归纳总结:可以发现,一般的四种命题的真假性,有且仅有以上的四种情况。(让学生课下举例子验证) 并且由于逆命题与否命题也是互为逆否命题,因此四种命题的真假性之间有以下关系:(教师引导,与学生一起归纳): ①两个命题互为逆否命题,它们有相同的真假性 ②两个命题为互逆命题或互否命题,它们的真假性没有关系 四种命题真假性之间的联系可以为我们进行推理论证带来方便,例如,由于原命题与其逆否命题有相同的真假性,当直接证明一个命题为真命题有困难时,可以通过证明其逆否命题为真命题来简介地证明原命题为真。 3.例题分析:证明:若,则.(教师引导学生板书教师点评) 三.小结: 四种命题的相互关系,以及它们之间的真假性关系,如何利用真假性关系进行推理证明。 四.作业: 板书: 原命题 逆命题 否命题 逆否命题 真 假 假 真 假 真 真 假 真 真 真 真 假 假 假 假 标题: 1.四种命题的相互关系 2.四种命题真假性之间的相互关系 例子 例题查看更多