- 2021-05-13 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学模拟试题及答案二
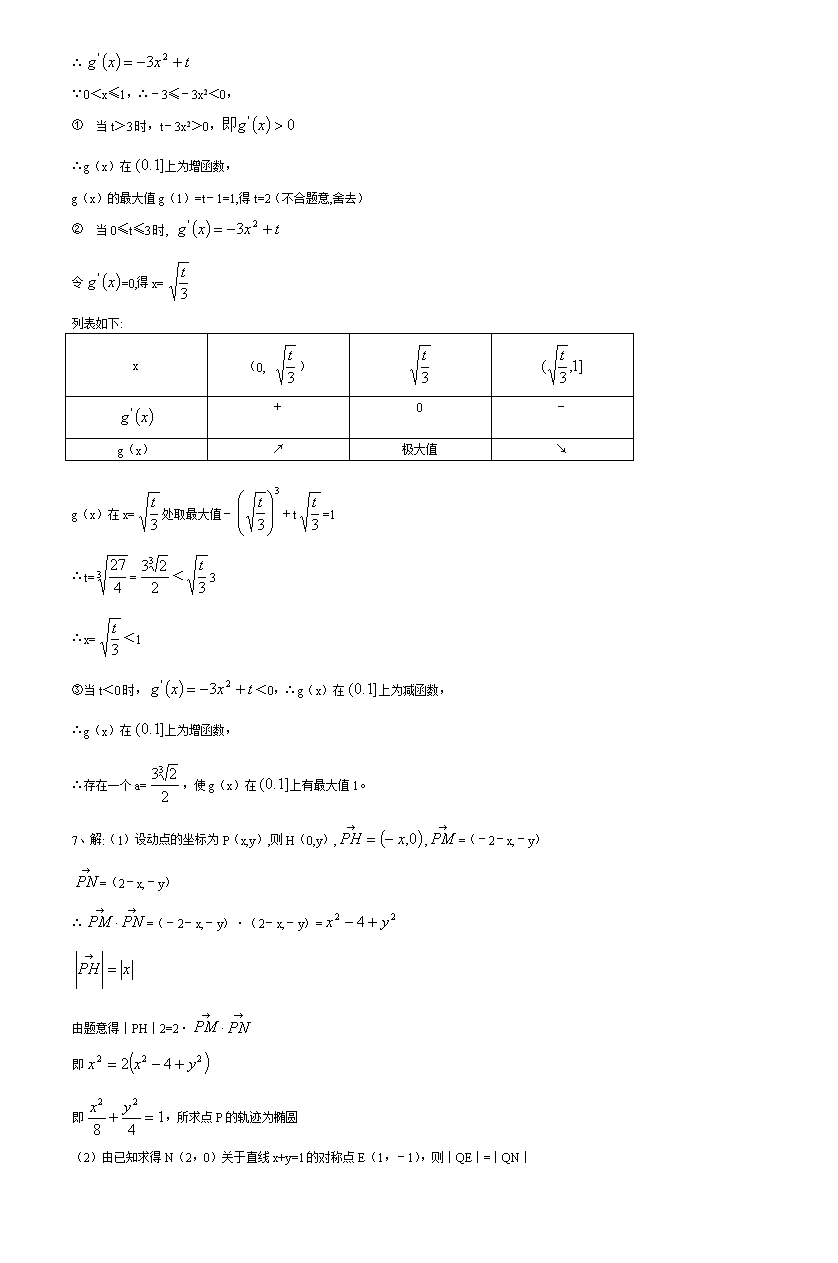
2012年高考数学模拟试题及答案(二) 6 已知过函数f(x)=的图象上一点B(1,b)的切线的斜率为-3。 (1) 求a、b的值; (2) 求A的取值范围,使不等式f(x)≤A-1987对于x∈[-1,4]恒成立; (3) 令。是否存在一个实数t,使得当时,g(x)有最大值1? 7 已知两点M(-2,0),N(2,0),动点P在y轴上的射影为H,︱︱是2和的等比中项。 (1) 求动点P的轨迹方程,并指出方程所表示的曲线; (2) 若以点M、N为焦点的双曲线C过直线x+y=1上的点Q,求实轴最长的双曲线C的方程。 8.已知数列{an}满足 (1)求数列{bn}的通项公式; (2)设数列{bn}的前项和为S n,试比较Sn与的大小,并证明你的结论. 9.已知焦点在轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点为圆心,1为半径的圆相切,又知C的一个焦点与A关于直线对称. (Ⅰ)求双曲线C的方程; (Ⅱ)设直线与双曲线C的左支交于A,B两点,另一直线经过M(-2,0)及AB的中点,求直线在轴上的截距b的取值范围; (Ⅲ)若Q是双曲线C上的任一点,为双曲线C的左,右两个焦点,从引的平分线的垂线,垂足为N,试求点N的轨迹方程. 10. 对任意都有 (Ⅰ)求和的值. (Ⅱ)数列满足:=+,数列是等差数列吗?请给予证明; 试比较与的大小. 参考答案: 6、解:(1)= 依题意得k==3+2a=-3, ∴a=-3 ,把B(1,b)代入得b= ∴a=-3,b=-1 (2)令=3x2-6x=0得x=0或x=2 ∵f(0)=1,f(2)=23-3×22+1=-3 f(-1)=-3,f(4)=17 ∴x∈[-1,4],-3≤f(x)≤17 要使f(x)≤A-1987对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1987 ∴A≥2004。 (1) 已知g(x)=- ∴ ∵0<x≤1,∴-3≤-3x2<0, ① 当t>3时,t-3x2>0, ∴g(x)在上为增函数, g(x)的最大值g(1)=t-1=1,得t=2(不合题意,舍去) ② 当0≤t≤3时, 令=0,得x= 列表如下: x (0, ) + 0 - g(x) ↗ 极大值 ↘ g(x)在x=处取最大值-+t=1 ∴t==<3 ∴x=<1 ③当t<0时,<0,∴g(x)在上为减函数, ∴g(x)在上为增函数, ∴存在一个a=,使g(x)在上有最大值1。 7、解:(1)设动点的坐标为P(x,y),则H(0,y),,=(-2-x,-y) =(2-x,-y) ∴·=(-2-x,-y)·(2-x,-y)= 由题意得∣PH∣2=2·· 即 即,所求点P的轨迹为椭圆 (2)由已知求得N(2,0)关于直线x+y=1的对称点E(1,-1),则∣QE∣=∣QN∣ 双曲线的C实轴长2a=(当且仅当Q、E、M共线时取“=”),此时,实轴长2a最大为 所以,双曲线C的实半轴长a= 又 ∴双曲线C的方程式为 8.(1) (2) 9.解:(Ⅰ)设双曲线C的渐近线方程为y=kx,则kx-y=0 ∵该直线与圆相切, ∴双曲线C的两条渐近线方程为y=±x.…………………………………………2分 故设双曲线C的方程为. 又双曲线C的一个焦点为 ∴,. ∴双曲线C的方程为.………………………………………………4分 (Ⅱ)由得. 令 直线与双曲线左支交于两点,等价于方程f(x)=0在上有两个不等实根. 因此 解得. 又AB中点为, ∴直线l的方程为.………………………………6分 令x=0,得. ∵, ∴ ∴.………………………………………………8分 (Ⅲ)若Q在双曲线的右支上,则延长到T,使, 若Q在双曲线的左支上,则在上取一点T,使. 根据双曲线的定义,所以点T在以为圆心,2为半径的圆上,即点T的轨迹方程是 ①…………………………………………10分 由于点N是线段的中点,设,. 则,即. 代入①并整理得点N的轨迹方程为.………………12分 10 解:(Ⅰ)因为.所以.……2分 令,得,即.……………4分 (Ⅱ) 又………………5分 两式相加 . 所以,………………7分 又.故数列是等差数列.………………9分 (Ⅲ) ………………10分 ………………12分 所以……………………………………………………………………14分查看更多