- 2021-05-13 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
平面向量高考理科数学总复习专题练习
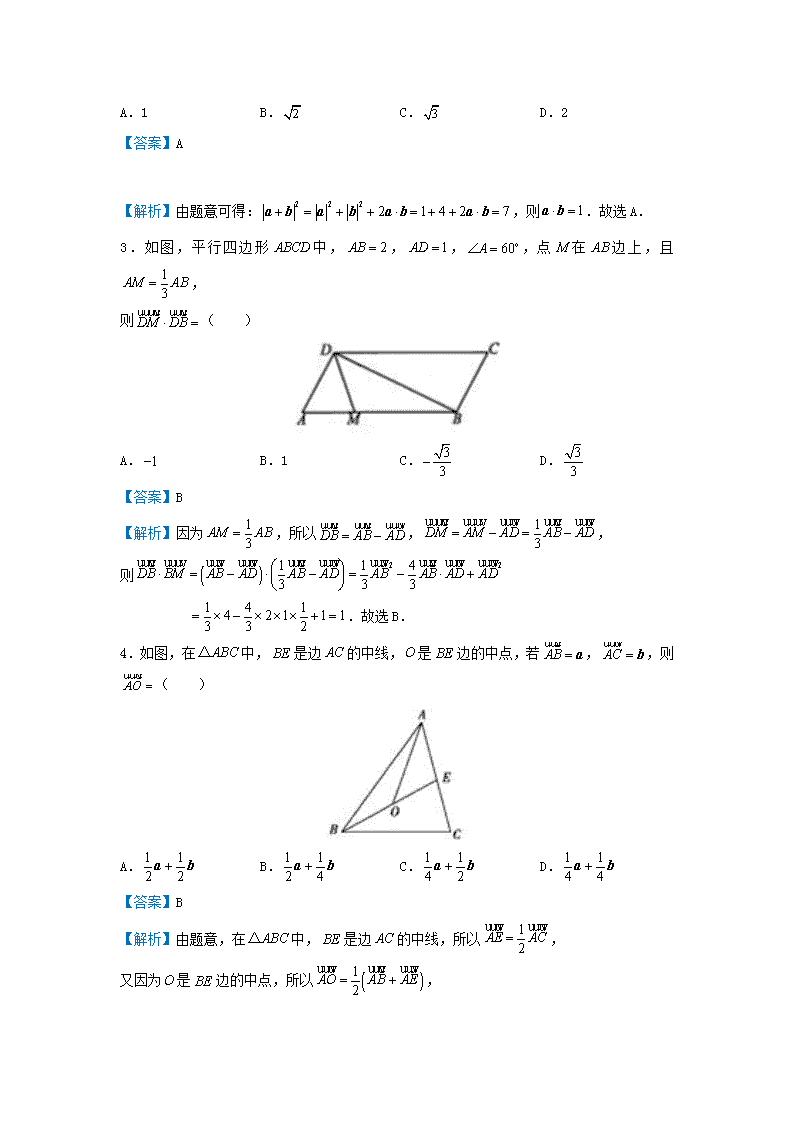
平面向量 1.代数法 例1:已知向量,满足,,且,则在方向上的投影为( ) A.3 B. C. D. 【答案】C 【解析】考虑在上的投影为,所以只需求出,即可. 由可得:, 所以.进而.故选C. 2.几何法 例2:设,是两个非零向量,且,则_______. 【答案】 【解析】可知,,为平行四边形的一组邻边和一条对角线, 由可知满足条件的只能是底角为,边长的菱形, 从而可求出另一条对角线的长度为. 3.建立直角坐标系 例3:在边长为1的正三角形中,设,,则__________. 【答案】 【解析】 上周是用合适的基底表示所求向量,从而解决问题,本周仍以此题为例,从另一个角度解题, 观察到本题图形为等边三角形,所以考虑利用建系解决数量积问题, 如图建系:,,, 下面求坐标:令,∴,, 由可得:,∴, ∴,,∴. 对点增分集训 一、单选题 1.已知向量,满足,,且向量,的夹角为,若与垂直,则实数的值为( ) A. B. C. D. 【答案】D 【解析】因为,所以,故选D. 2.已知向量,满足,,,则( ) A.1 B. C. D.2 【答案】A 【解析】由题意可得:,则.故选A. 3.如图,平行四边形中,,,,点在边上,且, 则( ) A. B.1 C. D. 【答案】B 【解析】因为,所以,, 则 .故选B. 4.如图,在中,是边的中线,是边的中点,若,,则( ) A. B. C. D. 【答案】B 【解析】由题意,在中,是边的中线,所以, 又因为是边的中点,所以, 所以,故选B. 5.在梯形中,,,,,动点和分别在线段和上,且,,则的最大值为( ) A. B. C. D. 【答案】D 【解析】因为,,,, 所以是直角梯形,且,, 以所在直线为轴,以所在直线为轴,建立如图所示的平面直角坐标系: 因为,,动点和分别在线段和上, 则,,,, 所以, 令且, 由基本不等式可知,当时可取得最大值, 则.故选D. 6.已知中,,,,为线段上任意一点,则的范围是( ) A. B. C. D. 【答案】C 【解析】根据题意,中,,,, 则根据余弦定理可得,即.∴ 为直角三角形 以为原点,为轴,为轴建立坐标系,则,, 则线段的方程为,. 设,则. ∵,∴.故选C. 7.已知非零向量,,满足且,则与的夹角为( ) A. B. C. D. 【答案】A 【解析】非零向量,,满足且,则, ∴,∴, ∴, ∴,,∴与的夹角为,故选A. 8.在中斜边,以为中点的线段,则的最大值为( ) A. B.0 C.2 D. 【答案】B 【解析】∵在中斜边,∴, ∵为线段中点,且, ∴原式, 当时,有最大值,.故选B. 9.设向量,,,满足,,,则的最大值等于 ( ) A.1 B. C. D.2 【答案】D 【解析】设,,,因为,, 所以,,所以,,,四点共圆, 因为,,所以, 由正弦定理知,即过,,,四点的圆的直径为2, 所以的最大值等于直径2,故选D. 10.已知与为单位向量,且,向量满足,则的取值范围为( ) A. B. C. D. 【答案】B 【解析】由,是单位向量,,可设,,, 由向量满足,∴, ∴,即,其圆心,半径, ∴,∴.故选B. 11.平行四边形中,,在上投影的数量分别为,,则在上的投影的取值范围是( ) A. B. C. D. 【答案】A 【解析】建立如图所示的直角坐标系:设, 则,,则,解得. 所以,.在上的摄影, 当时,,得到:,当时,,,故选A. 12.如图,在等腰直角三角形中,,,是线段上的点,且,则的取值范围是( ) A. B. C. D. 【答案】A 【解析】如图所示,以所在直线为轴,以的中垂线为轴建立平面直角坐标系, 则,,,设,则,. 据此有,, 则. 据此可知,当时,取得最小值; 当或时,取得最大值; 的取值范围是.故选A. 二、填空题 13.已知向量,,,若,则________. 【答案】. 【解析】因为,,所以, 又,且,则,即. 14.若向量,满足,,且,则与的夹角为__________. 【答案】 【解析】由得,,即, 据此可得,∴, 又与的夹角的取值范围为,故与的夹角为. 15.已知正方形的边长为2,是上的一个动点,则求的最大值为________. 【答案】4 【解析】设,则, 又, ∴, ∵,∴当时,取得最大值4,故答案为4. 16.在中,,,,为线段上一点,则的取值范围为____. 【答案】 【解析】以为坐标原点,,所在直线为,轴建立直角坐标系, 可得,,,则直线的方程为, 设,则,,,, 则| , 由,可得的最小值为 ,时,则的最大值为 即的取值范围为.故答案为.查看更多