- 2021-05-13 发布 |
- 37.5 KB |
- 19页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
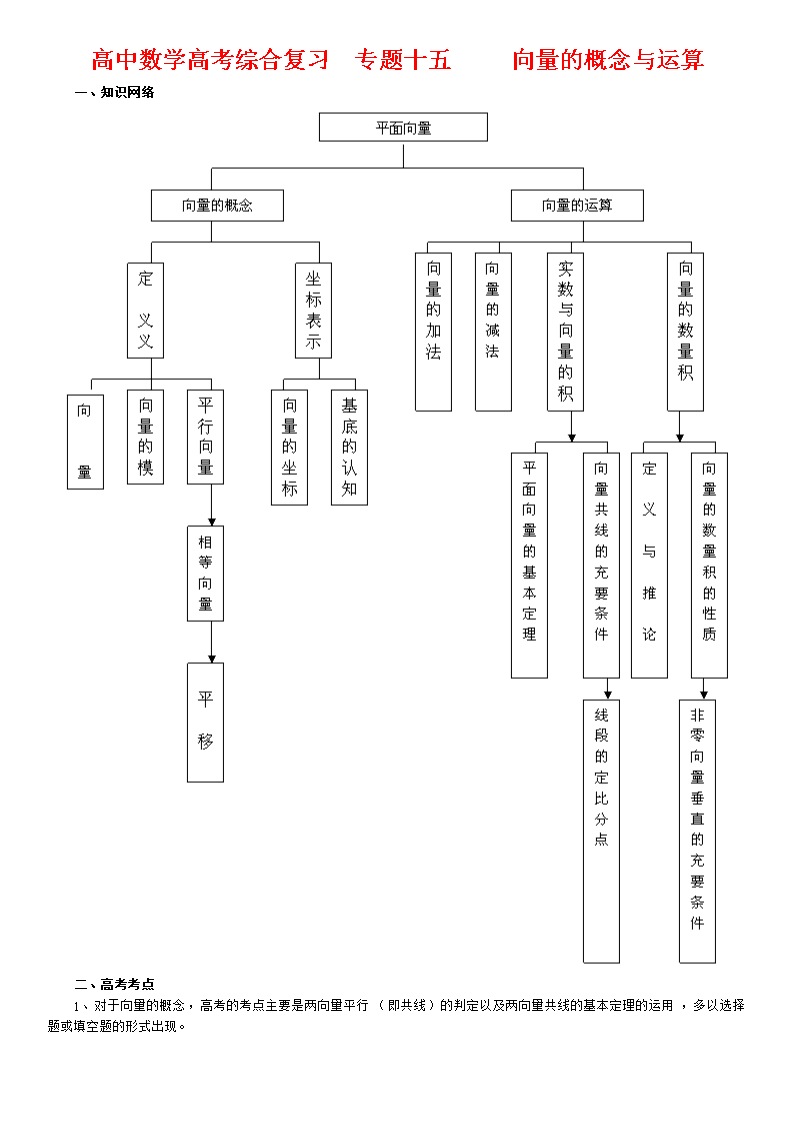
北京四中高中数学高考综合复习 专题十五 向量的概念与运算
高中数学高考综合复习 专题十五 向量的概念与运算 一、知识网络 二、高考考点 1、对于向量的概念,高考的考点主要是两向量平行(即共线)的判定以及两向量共线的基本定理的运用,多以选择题或填空题的形式出现。 2、对于向量的运算,向量的数量积及其运算是向量的核心内容,对此,高考的考点主要是: (1)向量的加法、减法的几何意义与坐标表示的应用; (2)向量共线的充要条件的应用; (3)向量垂直的充要条件的应用; (4)向量的夹角的计算与应用; (5)向量的模的计算,关于向量的模的等式的变形与转化,关于向量的模的不等式的认知与转化。 3、线段的定比分点线或平移问题。 4、以向量为载体的三角求值或图象变换问题,以向量为载体的函数或解析几何问题(多以解答题的形式出现)。 三、知识要点 (一)向量的概念 1、定义 (1)向量:既有大小又有方向的量叫做向量。 (2)向量的模:向量 的大小(即长度)叫做向量 的模,记作 。 特例:长度为0的向量叫做零向量,记作 ;长度为1的向量叫做单位向量. (3)平行向量(共线向量): 一般定义:方向相同或相反的非零向量叫做平行向量,平行向量也叫做共线向量. 特殊规定: 与任一向量平行(即共线). (4)相等向量:长度相等且方向相同的向量叫做相等向量。 零向量与零向量相等。 认知:向量的平移具有“保值性”。 2、向量的坐标表示 (1)定义:在直角坐标系内,分别取与x轴、y轴正方向相同的两个单位向量 、 作为基底,任作一个向量 ,则由平面向量基本定理知,有且只有一对实数x,y使得 ,将有序实数对(x,y)叫做向量 的坐标,记作 ;并将 叫做向量 的坐标表示。 (2)认知:相等的向量,其坐标也相同,反之成立。 (二)向量的运算 1、向量的加法 2、向量的减法 3、实数与向量的积 (1)定义 (2)实数与向量的积的运算律: (3)平面向量的基本定理: 如果 是同一面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数 1, 2使 ,这两个不共线的向量 叫做表示这一平面内所有向量的一组基底。 (4)向量共线的充要条件: (i)向量与非零向量 共线 有且只有一个实数 使 (ii) 设 则: 4、向量的数量积(内积) (1)定义: (i)向量的夹角:已知两个非零向量 和 ,作 叫做向量 与 的夹角。 (ii)设两个非零向量 和 的夹角为 ,则把数量 叫做 与 的数量积(内积),记作 ,即 并且规定:零向量与任一向量的数量积为0. (2)推论 设 、 都是非零向量,则 (i) (ii) (iii) (3)坐标表示 (i) 设非零向量 ,则 (ii)设 (4)运算律(自己总结,认知) 四、经典例题 例1.判断下列命题是否正确: (1)若 的方向相同或相反; (2)若 (3)若 则A、B、C、D四点组成的图形为梯形; 分析: (1)不正确 ∵ 不能比较方向。 (2)不正确 当 时,虽然对任意 , 都有 不一定平行。 (3)不正确 ,故这里的已知条件也包含A、B、C、D四点共线的情形。 点评:判断或证明向量的共线或垂直问题,务必要注意有关向量为零向量的情形,判断失误或解题出现疏露,多是零向量惹的祸。 例2.设点O为ΔABC所在平面内一点 (1)若 ,则O为ΔABC的( ) A、外心 B、内心 C、垂心 D、重心 (2)若 ,则 为ΔABC的( ) A、外心 B、内心 C、重心 D、重心 (3)若动点P满足 ,则点P的轨迹一定通过ΔABC的( ) A、外心 B、内心 C、重心 D、重心 (4)若动点P满足 ,则点P轨迹一定通过ΔABC的( ) A、外心 B、内心 C、重心 D、重心 分析: (1)借助向量加法分析已知条件: 以 、 为邻边作平行四边形OBDC,并设OD∩BC=E,则由平行四边形性质知,E为BC和OD中点。 ① 且 ② ∴ 由①、②得 ∴A、O、E、D、四点共线 ③ 且 ④ 于是由③、④知O为ΔABC的重心,应选D (2)由 同理可得OA⊥BC,OC⊥AB 于是可知,O为ΔABC的垂心,应选C (3)由已知得 ① 令 ,则 是 上的单位向量,令 ,则 是 上的单位向量。 ∴由①得: ② 令 ,则点Q在角A的平分线上 ③ 又由②知的 与 共线且同向(或 ) ∴动点P在角A的平分线上 ∴点P的轨迹一定通过ΔABC的内心,应选B。 (4)注意到 的几何意义, =0 又由已知的得: ∴动点P在BC边的高线上 ∴动点P的轨迹一定通过ΔABC的垂心,应选C。 点评:品味各小题,从中参悟解题思路以及三角形的各心的向量特征。 例3: (1) 成立的充分必要条件为( ) A、 B、 C、 D、 (2)已知A、B、C三点共线,O为该直线外一点,设 且存在实数m使 , 则点A分 所成的比为( ) A、- B、2 C、 D、-2 分析: (1)注意到不等式 ,当且仅当 、 反向或 、 中至少有一个为 时等号成立, ∴由 得 、 反向或 由此否定A、B、C,本题应选D (2)注意到条件的复杂以及已知式变形方向的迷茫,故考虑从“目标 ”分析切入,主动去沟通“已知”, 设 则 (刻意变形,靠拢已知) (目标的延伸) ① 又由已知得: (已知的变形或延伸) ② ∴根据两向量相等的条件由①、②得: 于是可知,点A分 所成 的比 ,应选 A 点评: (i)(1)对任意向量 、 都有 ,其中,当且仅当 同向或 中至少有一个为 时左边的等号成立;当且仅当 反向或 中至少有一个为 时右边的等号成立;当且仅当 中至少有一个为 时,左右两等号同时成立。 (ii)对于(2),“已知”与“目标”相互靠扰,只是切入点是从“已知”切入还是从“目标”切入,需要仔细分析。 例4:设 、 分别是平面直角坐标系内x轴、y轴正方向上的两个单位向量,在同一条直线上有A、B、C三点, ,求实数m、n的值。 解:由题设知 与 共线 ① 又 ② ②代入①得: 7(2n-1)=(n+2)(2n+1) (n-3)(2n-3)=0 当 时代入②得: m=3 当 时代入②得:m=6 ∴ m=6,n=3或m=3, 点评:不失时机地利用向量的坐标表示,是解题的基本技巧。 例5. 设 试求满足: (这里O为原点) 分析:注意到 的坐标即点D的坐标,可从设 坐标,由(x,y)切入,去 建立关于x,y的方程组。 解:设 ,则点D坐标为(x,y) 则由已知条件 得: x-2y+1=0 ① 由 得: x+4=3(y-1) x-3y+7=0 ② 于是将①、②联立,解得: 点评:本题是对向量坐标的概念,向量的垂直与向量的平行的充要条件的综合应用,借此练习,可进一步认识与把握关于向量的概念与公式。 例6. 设向量 满足 (1)若 ,求 与 的夹角; (2)若 的值。 解: (1)设 与 的夹角为 ,则 ① ② 于是由②代入①得 : 注意到 ∈ [O, ],可得结果 (2)解法(着眼于对 等各个击破) 一方面由已知得: ③ 又 ④ 由③、④得 ⑤ 注意到 ,当且仅当 , 同向或 , 中至少有一个为 时等号成立 由⑤得 与 同向 另一方面,又由 知, 与 反向 与 的夹角为0°, 与 的夹角为180°, 与 的夹角为180° ∴原式 =3×1-1×4-3×4=-13 解法二(着眼于寻求目标与已知的整体联系): ∴由已知条件得 解法三(从寻求目标局部的值切入): 原式 同理, 点评:解法二与解法三,均着眼于整体代入,解题过程简明,比解法一有明显优势。但是,解法一中对已知数值的利用,却对今后的条件求值有着不可替代的潜在作用,条件求值中对已知数据的应用主要有以下三个方面: (1)利用数值本身(代入); (2)分别利用数值的绝对值和符号; (3)利用有关数值的关系沟通有关元素间的联系(比如,由3+1=4,32+42=52沟通联系等)。 例7.已知 的夹角为120°,且 ,试求m,n及 与 的夹角。 解法一:(利用内积的定义),设 与 的夹角为 , 由 再 ① ② 再由: 由①,②得 ③ 将③代入②得: ④ 于是由①,③,④得所求 ,n=-4, 的夹角为30°或150° 点评1:本题已知条件繁多,头绪纷乱,更需要在解题时梳理思绪。注意到所求m、n含在 中,故在求出 、 的值之后,以 的变形为主线展开求索: 变形1. 变形2. 变形3. 于是,整个解题过程既显得有条不紊,又感觉酣畅淋漓。 解法二(利用向量的坐标): 设 , 与 的夹角为 , 由已知得 ① 由 ② 又x12+y12=8 ③ x22+y22=4 ④ 由①,③解得 或 由②,④解得 或 将上述 , 坐标分四次代入 便解得n=-4, , =30°或150° 点评2:本解法致力于求 与 的坐标,虽然解题过程仍然曲折,但思路明朗,更多几分胜算。 例8. 设 的夹角为 , 分析:此题为以向量为载体的三角求值问题,因此,从化简 , 的坐标切入,向三角函数中常见的关系式转化。 解: ① ② ③ 注意到这里 由②、③得到 ④ ⑤ 于是由①、④得 由①、⑤得 解得 ⑥ 因此由⑥得 点评:在这里,利用实数与向量的乘法的法则,将 表为 ,从而为简化 及 的表达式以及简化 的表达式奠定良好的基础。 五、高考填题 (一)选择题、 1、(2005·湖南卷)P是ΔABC所在平面上一点,且 ,则P是ΔABC的( ) A、外心 B、内心 C、重心 D、垂心 分析: 由 同理,AB⊥PC,BC⊥PA 点P为ΔABC的垂心,应选D 2、(2005•山东卷)已知向量 , ,且 ,则一定共线的三点是( ) A.A、B、D B.A、B、C C.B、C、D D.A、C、D 分析: 利用两向量共线的充要条件来判定,从寻找所给向量的联系切入 由题意得 A、B、D三点共线,应选A 3、(2005•全国卷B)已知点A( ,1),B(0,0),C( ,0),设∠BAC的平分线AE与BC相交于E,那么有 ,其中 等于( ) A、 2 B、 C、-3 D、- 分析: 从认知目标切入,由题设易知 与 反向,故 <0 ① 又由三角形内角平分线定理得 即 =3 ② 于是由①、②得 =-3,应选C 4、(2005·北京卷)若 , , ,则向量 与 的夹角为( ) A、30° B、60° C、120° D、150° 分析: 令向量 与 的夹角为 ,则 ① 又由 得 ② 于是将已知与②代入①得 所得 ,应选C 5、(2005·福建)在ΔABC中, , , ,则k的值是( )。 A、5 B、-5 C、 D、 分析: 循着一般思路,欲求k的值,先寻找关于k的方程,可以通过解方程获取k的值,为此我们利用题设条件寻找等量关系切入: 由题设知 , 由此得(2,3)·(2-k,2)=0 2(2-k)+6=0 解得k=5,故应选A。 6、(2005·重庆)设向量 等于( )。 A、(1,1) B、(-4,-4) C、-4 D、(-2,-2) 分析: 循着向量的坐标表示与有关公式得: ∴ 原式=-4(1,1)=(-4,-4),应选B 7、(2005·重庆卷)已知A(3,1),B(6,1),C(4,3),D为线段BC的中点,则向量 与 的夹角为( ) A、 分析1: (特征分析法):画出ΔABC及其中线AD,又将向量 平移到 ,则可见 与 成钝角,而选项中A、B为锐角,D为负角,故只能选C。 分析2: (直接法):由题设D(5,2) 所求两向量夹角应为 ),应选C 8、(2005·浙江) 已知向量 ,满足对任意t∈R, ,则( ) A、 分析: 从已知不等式的等价变形切入,去认识所含向量 , 的关系 由已知得 整理得 ① 注意到①对任意 都成立。 即 ② 根据②式检验选项,故选C 点评:关于向量的模的不等式,变形转化的基本手段是不等式两边平方,这是本题切入、转化的关键环节。 (二)填空题 1、(2005·广东卷) 已知向量 分析: 注意到两向量平行的充要条件, 由已知条件得 2×6-3x=0,由此解得 x=4 2、(2005·全国卷C) 已知向量 ,且A、B、C三点共线,则k= 。 分析: 由A、B、C三点共线切入,向着向量的共线转化 A、B、C三点共线 向量 、 共线 又 由 、 共线的充要条件得 7(-k-4)=5(k-4),解为 3、(2005·天津卷)已知 =2, =4, 与 的夹角为 ,以 , 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为 。 分析: 根据向量加法与向量减法的几何意义又知, 、 分别表示上述平行四边形中两条对角线的长度。 注意到 与 的夹角为锐角,故此平行四边形的两条对角线中较短一条的长度为 ① 又 =4+16-2×2×4cos =12 ∴ =2 ② 于是由①、②知所求为 . 4、(2005·湖北卷)已知向量 =(-2,2), =(5,k),若 不超过5,则k的取值范围为 . 分析: 由已知得 若 ≤5,则9+(k+2)2≤25 ∴由此解得-6≤k≤2,故应填[-6,2] 5、(2004·浙江卷)已知平面上三点A、B、C满足 , , ,则 的值等于 。 分析: 从认知ΔABC切入,由32+42=52知 , ∴ ∴原式= = = =-25 6、(2005·全国卷A)ΔABC的外接圆圆心为0,两条边上的高的交点为H, =m( + + ),则实数m= 。 分析: 由题设知,O为ΔABC的外心,即O是ΔABC的三边中垂线的交点,因此,以 与 为邻边作平行四边形OADC,则OADC为菱形,且 + = ∴ ⊥ ⊥( + ) ∴ + + 的终点必在AC边的高线上 ① 同理, + + 的终点在AB边的高线上 ② ∴由①、②得 + + 的终点为△ABC的垂心H. ∴ ∴m=1 点评:从O为ΔABC的外心切入,认知向量 ,此乃求解本题的关键。 三、解答题 1、(2005·山东卷)已知向量 =(cos 、sin )和 =( - sin ,cos ), ,且 = ,求cos( + )的值。 分析:这是以向量为载体的三角求值问题,故首先要利用向量的有关概念与公式进行转化-化生为熟,进入三角函数求值的“似曾相识燕归来”的境界。 解:由已知得 由题设 ① 又 ② 由①、②得 ③ ④ 于是由③、④得 点评:首先运用向量的公式化生为熟,进而运用“方程思想”去求解 的值,这是求解本题所运用的基本策略。也是解决本类问题的基本思路 2、(2005·江西卷) 已知向量 ,是否存在实数 x∈[O, ],使f(x)+f′(x)=0 (其中f′(x)是f(x)的 导函数)若存在,则求出x的值;若不存在,则证明。 分析:对于这样以平面向量为载体的 问题,首先仍是运用向量的知识将其转化为熟悉的三角函数问题。 解: =sinx+cosx ∴f (x)=cosx-sinx 若f(x)+f (x)=0,则2cosx=0即cosx=0 由x∈[0,π] 又由题意: 综上:[0,π]内不存在f(x)+f (x)=0的x值。 点评:函数式的变形要注意保持等价性,特别是在变形过程中不可改变函数的定义域,由①到②,需要附加 的制约,以保证函数的定义域不发生变更. 3、(2004·福建卷)设 (1)若 (2)若 函数 y=2sin2x的图象按向量 平移后得到函数y=f(x)的图象,求实数m、n的值。 解: (1)由题设得 由①、②得 (2) 函数 y=2sin2x按向量 平移后得到函数y=2sin2(x-m)+n的图象。 由题设 即 又 ∴ 点评:函数y=f(x)的图象按向量 平移后所得图象的函数解析式由y-k=f(x-h)确定,上面求解利用了这一结论。 查看更多