云南省高考数学一模试卷理科

云南省高考数学一模试卷理科

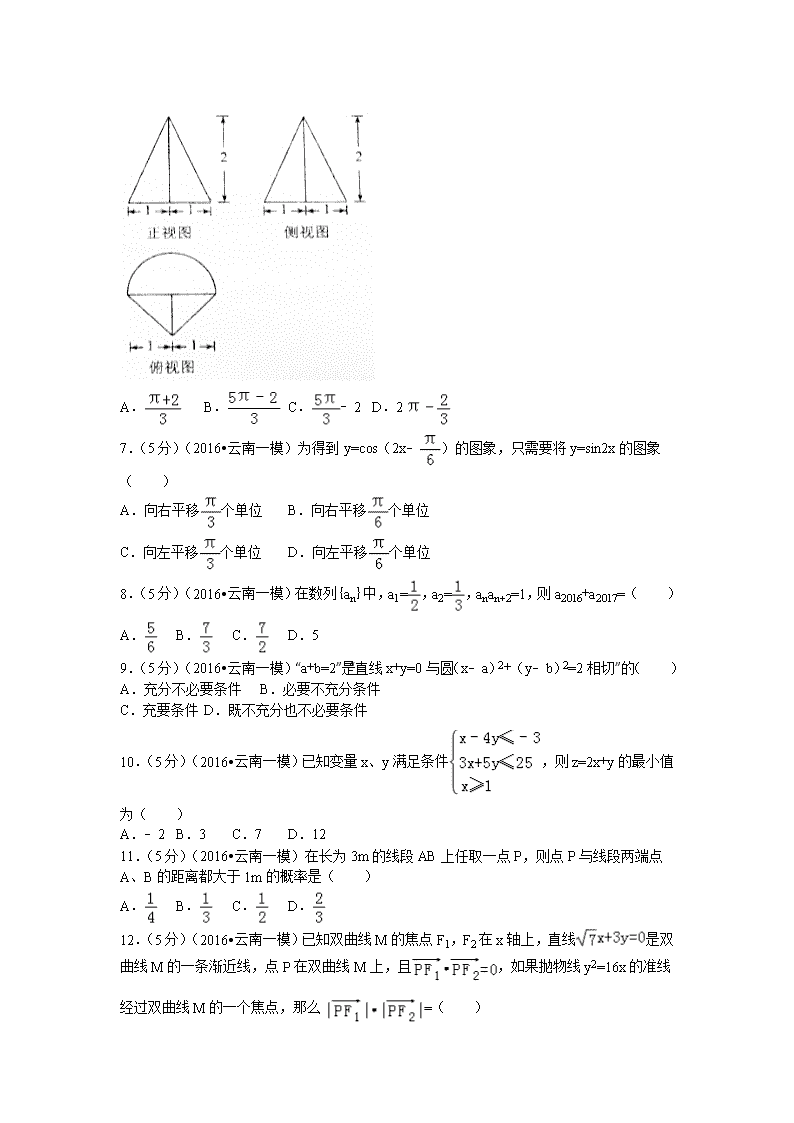
‎2016年云南省高考数学一模试卷（理科）‎ ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）（2016•云南一模）已知i为虚数单位，复数z1=1+i，z2=1﹣i，则=（　　）‎ A． B． C．﹣i D．i ‎2．（5分）（2016•云南一模）已知平面向量，如果，那么=（　　）‎ A． B． C．3 D．‎ ‎3．（5分）（2016•云南一模）函数y=2sinxcosx﹣2sin2x的最小值为（　　）‎ A．﹣4 B． C． D．﹣2‎ ‎4．（5分）（2016•云南一模）（﹣+）10的展开式中x2的系数等于（　　）‎ A．45 B．20 C．﹣30 D．﹣90‎ ‎5．（5分）（2016•云南一模）若运行如图所示程序框图，则输出结果S的值为（　　）‎ A．94 B．86 C．73 D．56‎ ‎6．（5分）（2016•云南一模）如图是底面半径为1，高为2的圆柱被削掉一部分后剩余的几何体的三视图（注：正视图也称主视图，侧视图也称左视图），则被削掉的那部分的体积为（　　）‎ A． B． C．﹣2 D．2‎ ‎7．（5分）（2016•云南一模）为得到y=cos（2x﹣）的图象，只需要将y=sin2x的图象（　　）‎ A．向右平移个单位 B．向右平移个单位 C．向左平移个单位 D．向左平移个单位 ‎8．（5分）（2016•云南一模）在数列{an}中，a1=，a2=，anan+2=1，则a2016+a2017=（　　）‎ A． B． C． D．5‎ ‎9．（5分）（2016•云南一模）“a+b=2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎10．（5分）（2016•云南一模）已知变量x、y满足条件，则z=2x+y的最小值为（　　）‎ A．﹣2 B．3 C．7 D．12‎ ‎11．（5分）（2016•云南一模）在长为3m的线段AB上任取一点P，则点P与线段两端点A、B的距离都大于1m的概率是（　　）‎ A． B． C． D．‎ ‎12．（5分）（2016•云南一模）已知双曲线M的焦点F1，F2在x轴上，直线是双曲线M的一条渐近线，点P在双曲线M上，且，如果抛物线y2=16x的准线经过双曲线M的一个焦点，那么=（　　）‎ A．21 B．14 C．7 D．0‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）（2016•云南一模）已知函数f（x）的定义域为实数集R，∀x∈R，f（x﹣90）=则f（10）﹣f（﹣100）的值为　　　　　　．‎ ‎14．（5分）（2016•云南一模）已知三棱锥P﹣ABC的顶点P、A、B、C在球O的表面上，△ABC是边长为的等边三角形，如果球O的表面积为36π，那么P到平面ABC距离的最大值为　　　　　　．‎ ‎15．（5分）（2016•云南一模）△ABC中，内角A、B、C对的边分别为a、b、c，如果△ABC的面积等于8，a=5，tanB=﹣，那么=　　　　　　．‎ ‎16．（5分）（2016•云南一模）已知实数a、b常数，若函数y=+be2x+1的图象在切点（0，）处的切线方程为3x+4y﹣2=0，y=+be2x﹣1与y=k（x﹣1）3的图象有三个公共点，则实数k的取值范围是　　　　　　．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）（2016•云南一模）设数列{an}的前n项和为Sn，对任意正整数n，3an﹣2Sn=2．‎ ‎（I）求数列{an}的通项公式；‎ ‎（Ⅱ）求证：Sn+2Sn＜．‎ ‎18．（12分）（2016•云南一模）某市教育与环保部门联合组织该市中学参加市中学生环保知识团体竞赛，根据比赛规则，某中学选拔出8名同学组成参赛队，其中初中学部选出的3名同学有2名女生；高中学部选出的5名同学有3名女生，竞赛组委会将从这8名同学中随机选出4人参加比赛．‎ ‎（Ⅰ）设“选出的4人中恰有2名女生，而且这2名女生来自同一个学部”为事件A，求事件A的概率P（A）；‎ ‎（Ⅱ）设X为选出的4人中女生的人数，求随机变量X的分布列和数学期望．‎ ‎19．（12分）（2016•云南一模）如图，在三棱锥A﹣BCD中，CD⊥BD，AB=AD，E为BC的中点．‎ ‎（I）求证：AE⊥BD；‎ ‎（Ⅱ）设平面ABD⊥平面BCD，AD=CD=2，BC=4，求二面角B﹣AC﹣D的正弦值．‎ ‎20．（12分）（2016•云南一模）已知焦点在y轴上的椭圆E的中心是原点O，离心率等于，以椭圆E的长轴和短轴为对角线的四边形的周长为4，直线l：y=kx+m与y轴交于点P，与椭圆E交于A、B两个相异点，且=λ．‎ ‎（I）求椭圆E的方程；‎ ‎（Ⅱ）是否存在m，使+λ=4？若存在，求m的取值范围；若不存在，请说明理由．‎ ‎21．（12分）（2016•云南一模）已知f（x）=2x+3﹣．‎ ‎（I）求证：当x=0时，f（x）取得极小值；‎ ‎（Ⅱ）是否存在满足n＞m≥0的实数m，n，当x∈[m，n]时，f（x）的值域为[m，n]？若存在，求m，n的值；若不存在，请说明理由．‎ ‎　‎ 请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-1：几何证明选讲]‎ ‎22．（10分）（2016•云南一模）如图，BC是⊙O的直径，EC与⊙O相切于C，AB是⊙O的弦，D是的中点，BD的延长线与CE交于E．‎ ‎（Ⅰ）求证：BC•CD=BD•CE；‎ ‎（Ⅱ）若，求AB．‎ ‎　‎ ‎[选修4-4：坐标系与参数方程]‎ ‎23．（2016•云南一模）在直角坐标系xOy中，直线l的参数方程为（t为参数）．在以原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=．‎ ‎（I）直接写出直线l、曲线C的直角坐标方程；‎ ‎（II）设曲线C上的点到直线l的距离为d，求d的取值范围．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．（2016•云南一模）已知f（x）=|x﹣2|+|x+1|+2|x+2|．‎ ‎（Ⅰ）求证：f（x）≥5；‎ ‎（Ⅱ）若对任意实数都成立，求实数a的取值范围．‎ ‎　‎ ‎2016年云南省高考数学一模试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）（2016•云南一模）已知i为虚数单位，复数z1=1+i，z2=1﹣i，则=（　　）‎ A． B． C．﹣i D．i ‎【解答】解：由z1=1+i，z2=1﹣i，‎ 得=，‎ 故选：D．‎ ‎　‎ ‎2．（5分）（2016•云南一模）已知平面向量，如果，那么=（　　）‎ A． B． C．3 D．‎ ‎【解答】解：∵；‎ ‎∴3•（﹣1）﹣6x=0；‎ ‎∴；‎ ‎∴；‎ ‎∴．‎ 故选B．‎ ‎　‎ ‎3．（5分）（2016•云南一模）函数y=2sinxcosx﹣2sin2x的最小值为（　　）‎ A．﹣4 B． C． D．﹣2‎ ‎【解答】解：y=2sinxcosx﹣2sin2x=sin2x﹣（1﹣cos2x）=sin2x+cos2x﹣1‎ ‎==，‎ ‎∴函数y=2sinxcosx﹣2sin2x的最小值为．‎ 故选：C．‎ ‎　‎ ‎4．（5分）（2016•云南一模）（﹣+）10的展开式中x2的系数等于（　　）‎ A．45 B．20 C．﹣30 D．﹣90‎ ‎【解答】解：（﹣+）10的展开式的通项公式为 Tr+1=•（﹣1）10﹣r•，‎ 令=2，求得r=2，可得展开式中x2的系数为=45，‎ 故选：A．‎ ‎　‎ ‎5．（5分）（2016•云南一模）若运行如图所示程序框图，则输出结果S的值为（　　）‎ A．94 B．86 C．73 D．56‎ ‎【解答】解：模拟执行程序，可得 i=1，S=1‎ i=2，S=4‎ 不满足条件i＞5，i=3，S=10，‎ 不满足条件i＞5，i=4，S=22，‎ 不满足条件i＞5，i=5，S=46，‎ 不满足条件i＞5，i=6，S=94，‎ 满足条件i＞5，退出循环，输出S的值为94．‎ 故选：A．‎ ‎　‎ ‎6．（5分）（2016•云南一模）如图是底面半径为1，高为2的圆柱被削掉一部分后剩余的几何体的三视图（注：正视图也称主视图，侧视图也称左视图），则被削掉的那部分的体积为（　　）‎ A． B． C．﹣2 D．2‎ ‎【解答】解：根据几何体的三视图，得；‎ 该几何体是底面半径为1，高为2的半圆锥体，‎ 与底面为等腰三角形高为2的三棱锥的组合体，‎ 其体积为•πr2h+Sh=π×12×2+××2×1×2=；‎ 又圆柱的体积为πr2h=π×12×2=2π，‎ 所以被削掉的那部分的体积为2π﹣=．‎ 故选：B．‎ ‎　‎ ‎7．（5分）（2016•云南一模）为得到y=cos（2x﹣）的图象，只需要将y=sin2x的图象（　　）‎ A．向右平移个单位 B．向右平移个单位 C．向左平移个单位 D．向左平移个单位 ‎【解答】解：∵y=cos（2x﹣）=sin（2x﹣+）=sin（2x+）=sin2（x+），‎ ‎∴将y=sin2x的图象向左平移个单位，可得y=cos（2x﹣）的图象，‎ 故选：D．‎ ‎　‎ ‎8．（5分）（2016•云南一模）在数列{an}中，a1=，a2=，anan+2=1，则a2016+a2017=（　　）‎ A． B． C． D．5‎ ‎【解答】解：∵a1=，a2=，anan+2=1，‎ ‎∴a3=2，a5=，…，可得：a4n﹣3=，a4n﹣1=2．‎ 同理可得：a4n﹣2=，a4n=3．‎ ‎∴a2016+a2017=3+=．‎ 故选：C．‎ ‎　‎ ‎9．（5分）（2016•云南一模）“a+b=2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【解答】解：若直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切 则圆心（a，b）到直线x+y=0的距离等于半径 即=，即|a+b|=2‎ 即a+b=±2‎ 故“a+b=2”是“直线x+y=0与圆（x﹣a）2+（y﹣b）2=2相切”的充分不必要条件 故选A ‎　‎ ‎10．（5分）（2016•云南一模）已知变量x、y满足条件，则z=2x+y的最小值为（　　）‎ A．﹣2 B．3 C．7 D．12‎ ‎【解答】解：如图即为满足不等式组的可行域，‎ 将交点分别求得为（1，1），（5，2），（1，）‎ 当x=1，y=1时，2x+y=3‎ 当x=1，y=时，2x+y=‎ 当x=5，y=2时，2x+y=12‎ ‎∴当x=1，y=1时，2x+y有最小值3．‎ 故选：B ‎　‎ ‎11．（5分）（2016•云南一模）在长为3m的线段AB上任取一点P，则点P与线段两端点A、B的距离都大于1m的概率是（　　）‎ A． B． C． D．‎ ‎【解答】解：设“长为3m的线段AB”对应区间[0，3]‎ ‎“与线段两端点A、B的距离都大于1m”为事件 A，则满足A的区间为[1，2]‎ 根据几何概率的计算公式可得，‎ 故选：B ‎　‎ ‎12．（5分）（2016•云南一模）已知双曲线M的焦点F1，F2在x轴上，直线是双曲线M的一条渐近线，点P在双曲线M上，且，如果抛物线y2=16x的准线经过双曲线M的一个焦点，那么=（　　）‎ A．21 B．14 C．7 D．0‎ ‎【解答】解：抛物线y2=16x的准线为x=﹣4，‎ 由题意可得双曲线M的一个焦点为（﹣4，0），‎ 设双曲线的方程为﹣=1（a，b＞0），‎ 可得c=4，即a2+b2=16，‎ 直线是双曲线M的一条渐近线，‎ 可得=，‎ 解得a=3，b=，‎ 可设P为右支上一点，由双曲线的定义可得 ‎|PF1|﹣|PF2|=2a=6，①‎ 由勾股定理可得，|PF1|2+|PF2|2=|F1F2|2=4c2=64，②‎ ‎②﹣①2，可得|PF1|•|PF2|=14．‎ 故选：B．‎ ‎　‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13．（5分）（2016•云南一模）已知函数f（x）的定义域为实数集R，∀x∈R，f（x﹣90）=则f（10）﹣f（﹣100）的值为　﹣8　．‎ ‎【解答】解：f（10）=f（100﹣90）=lg100=2，‎ f（﹣100）=f（﹣10﹣90）=﹣（﹣10）=10．‎ ‎∴f（10）﹣f（﹣100）=2﹣10=﹣8．‎ 故答案为：﹣8．‎ ‎　‎ ‎14．（5分）（2016•云南一模）已知三棱锥P﹣ABC的顶点P、A、B、C在球O的表面上，△ABC是边长为的等边三角形，如果球O的表面积为36π，那么P到平面ABC距离的最大值为　　．‎ ‎【解答】解：△ABC是边长为的等边三角形，外接圆的半径为1，‎ 球O的表面积为36π，球的半径为3，∴球心O到平面ABC的距离为=2，‎ ‎∴P到平面ABC距离的最大值为．‎ 故答案为：．‎ ‎　‎ ‎15．（5分）（2016•云南一模）△ABC中，内角A、B、C对的边分别为a、b、c，如果△ABC的面积等于8，a=5，tanB=﹣，那么=　　．‎ ‎【解答】解：△ABC中，∵tanB=﹣，∴sinB=，cosB=﹣．‎ 又S==2c=8，∴c=4，‎ ‎∴b==．‎ ‎∴==．‎ 故答案为：．‎ ‎　‎ ‎16．（5分）（2016•云南一模）已知实数a、b常数，若函数y=+be2x+1的图象在切点（0，）处的切线方程为3x+4y﹣2=0，y=+be2x﹣1与y=k（x﹣1）3的图象有三个公共点，则实数k的取值范围是　（﹣∞，﹣）∪（0，+∞）　．‎ ‎【解答】解：当x＜1时，函数y=+be2x+1=+be2x+1，‎ 则函数的导数f′（x）=+2be2x+1，‎ ‎∵若函数y=y=+be2x+1的图象在切点（0，）处的切线方程为3x+4y﹣2=0，‎ ‎∴f（0）=，且f′（0）=﹣，‎ 即a+be=，﹣a+2be=﹣，得a=1，b=0，‎ 即y=+be2x+1=，‎ 由=k（x﹣1）3得当x=1时，方程成立，‎ 当x≠1时，若x＞1得=k（x﹣1）3得=k（x﹣1）2，‎ 若x＜1得﹣=k（x﹣1）3得﹣=k（x﹣1）2，‎ 若k=0，则两个方程无解，‎ 若k＞0时，作出对应函数的图象如右图：‎ 此时满足当x＞1时，有一个交点，‎ 当x＜1时，有一个交点，‎ 此时满足两个函数共有3个交点．‎ 若k＜0时，作出对应函数的图象如图：‎ 此时满足当x＞1时，没有交点，‎ 当x＜1时，则需要有2个交点，‎ 由﹣=k（x﹣1）2，‎ 得k（x+2）（x﹣1）2+1=0，x＜1，‎ 设g（x）=k（x+2）（x﹣1）2+1，‎ 则g′（x）=3k（x﹣1）（x+1），x＜1，k＜0，‎ 由g′（x）=0，x=﹣1，‎ 当x＜﹣1时，g′（x）＜0，‎ 当﹣1＜x＜1时，g′（x）＞0，‎ 即当x=﹣1函数取得极小值g（﹣1）=4k+1，‎ 要使当x＜1时，则g（x）要有2个交点，‎ 则极小值g（﹣1）=4k+1＜0，得k＜﹣，‎ 此时满足两个函数共有3个交点．‎ 综上k的取值范围是k＞0或k＜0，‎ 故答案为：（﹣∞，﹣）∪（0，+∞）．‎ ‎　‎ 三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17．（12分）（2016•云南一模）设数列{an}的前n项和为Sn，对任意正整数n，3an﹣2Sn=2．‎ ‎（I）求数列{an}的通项公式；‎ ‎（Ⅱ）求证：Sn+2Sn＜．‎ ‎【解答】（I）解：∵对任意正整数n，3an﹣2Sn=2，∴3a1﹣2a1=2，解得a1=2．‎ 当n≥2时，3an﹣1﹣2Sn﹣1=2，可得3an﹣3an﹣1﹣2an=0，化为an=3an﹣1，‎ ‎∴数列{an}是等比数列，公比为3，首项为2．‎ ‎∴an=2×3n﹣1．‎ ‎（2）证明：由（I）可得：Sn==3n﹣1．‎ ‎∴Sn+2Sn﹣=（3n+2﹣1）（3n﹣1）﹣（3n+1﹣1）2=﹣4×3n＜0，‎ ‎∴Sn+2Sn＜．‎ ‎　‎ ‎18．（12分）（2016•云南一模）某市教育与环保部门联合组织该市中学参加市中学生环保知识团体竞赛，根据比赛规则，某中学选拔出8名同学组成参赛队，其中初中学部选出的3名同学有2名女生；高中学部选出的5名同学有3名女生，竞赛组委会将从这8名同学中随机选出4人参加比赛．‎ ‎（Ⅰ）设“选出的4人中恰有2名女生，而且这2名女生来自同一个学部”为事件A，求事件A的概率P（A）；‎ ‎（Ⅱ）设X为选出的4人中女生的人数，求随机变量X的分布列和数学期望．‎ ‎【解答】解：（Ⅰ）∵中学选拔出8名同学组成参赛队，其中初中学部选出的3名同学有2名女生；‎ 高中学部选出的5名同学有3名女生，竞赛组委会将从这8名同学中随机选出4人参加比赛，‎ 设“选出的4人中恰有2名女生，而且这2名女生来自同一个学部”为事件A，‎ 由已知，得，‎ 所以事件A的概率为．…（5分）‎ ‎（Ⅱ）随机变量X的所有可能取值为1，2，3，4．‎ 由已知得．…（8分）‎ P（X=1）==，‎ P（X=2）==，‎ P（X=3）==，‎ P（X=4）==，‎ 所以随机变量X的分布列为：‎ X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎…（10分）‎ 随机变量X的数学期望．…（12分）‎ ‎　‎ ‎19．（12分）（2016•云南一模）如图，在三棱锥A﹣BCD中，CD⊥BD，AB=AD，E为BC的中点．‎ ‎（I）求证：AE⊥BD；‎ ‎（Ⅱ）设平面ABD⊥平面BCD，AD=CD=2，BC=4，求二面角B﹣AC﹣D的正弦值．‎ ‎【解答】证明：（I）∵AB=AD，E为BC的中点，‎ ‎∴取BD的中点0，‎ 连接AO，OE，‎ 则OA⊥BD，OE是△BCD的中位线，‎ ‎∴OE∥CD，‎ ‎∵CD⊥BD，∴OE⊥BD，‎ ‎∵BD∩OA=O，‎ ‎∴AE⊥BD；‎ ‎（Ⅱ）设平面ABD⊥平面BCD，‎ ‎∵OA⊥BD，∴OA⊥面BCD，‎ 建立以O为坐标原点，OE，OD，OA分别为x，y，z轴的空间直角坐标系如图：‎ ‎∵AD=CD=2，BC=4，‎ ‎∴OA=OB=OD=，OE=1，‎ 则B（0，﹣，0），D（0，，0），E（1，0，0），A（0，0，），C（2，，0），‎ 则=（0，，），=（2，，﹣），=（﹣2，0，0），‎ 设平面ABC的一个法向量为=（x，y，z），‎ 则，‎ 令y=1，则z=﹣1，x=﹣，即=（﹣，1，﹣1），‎ 设平面ACD的一个法向量为=（x，y，z），‎ 则，‎ 令y=1，则z=1，x=0，则=（0，1，1），‎ cos＜，＞==0，‎ 即＜，＞=90°‎ 则二面角B﹣AC﹣D的正弦值sin90°=1．‎ ‎　‎ ‎20．（12分）（2016•云南一模）已知焦点在y轴上的椭圆E的中心是原点O，离心率等于，以椭圆E的长轴和短轴为对角线的四边形的周长为4，直线l：y=kx+m与y轴交于点P，与椭圆E交于A、B两个相异点，且=λ．‎ ‎（I）求椭圆E的方程；‎ ‎（Ⅱ）是否存在m，使+λ=4？若存在，求m的取值范围；若不存在，请说明理由．‎ ‎【解答】解：（I）设椭圆的方程为+=1（a＞b＞0），‎ 由题意可得e==，4=4，‎ a2﹣b2=c2，‎ 解得a=2，b=1，c=，‎ 即有椭圆的方程为+x2=1；‎ ‎（Ⅱ）=λ，可得﹣=λ（﹣），‎ ‎+λ=（1+λ），‎ 由+λ=4，可得λ=3，‎ 由题意可得P（0，m），且﹣2＜m＜2，‎ 设A（x1，y1），B（x2，y2），‎ 由=3，可得﹣x1=3x2，①‎ 由直线y=kx+m代入椭圆方程y2+4x2=4，‎ 可得（4+k2）x2+2kmx+m2﹣4=0，‎ 即有x1+x2=﹣，x1x2=，②‎ 由①②可得m2==1+，‎ 由1+k2≥1，可得0＜≤3，‎ 即有1＜m2≤4，由于m∈（﹣2，2），‎ 当m=0时，O，P重合，λ=1显然成立．‎ 可得m的取值范围是（﹣2，﹣1）∪（1，2）∪{0}．‎ ‎　‎ ‎21．（12分）（2016•云南一模）已知f（x）=2x+3﹣．‎ ‎（I）求证：当x=0时，f（x）取得极小值；‎ ‎（Ⅱ）是否存在满足n＞m≥0的实数m，n，当x∈[m，n]时，f（x）的值域为[m，n]？若存在，求m，n的值；若不存在，请说明理由．‎ ‎【解答】解：（I）由2x+1＞0得x＞﹣，‎ 函数的导数f′（x）=2﹣=2﹣=‎ ‎=，‎ 设g（x）=8x2+8x+2ln（2x+1），‎ 则g′（x）=16x+8+=8（2x+1）+，‎ ‎∵2x+1＞0，‎ ‎∴g′（x）＞0，‎ 即g（x）在x＞﹣上为增函数，‎ ‎∵g（0）=0，‎ ‎∴当x＞0时，g（x）＞g（0）=0，此时f′（x）＞0，函数f（x）递增，‎ 当x＜0时，g（x）＜g（0）=0，此时f′（x）＜0，函数f（x）递减，‎ 故当x=0时，f（x）取得极小值；‎ ‎（Ⅱ）由（Ⅰ）知当x＞0时，函数f（x）递增，‎ 若存在满足n＞m≥0的实数m，n，当x∈[m，n]时，f（x）的值域为[m，n]，‎ 则满足，即m，n是方程f（x）=x的两个不同的根，‎ 即2x+3﹣=x，‎ 则x+3=．‎ 即（x+3）（2x+1）=ln（2x+1），‎ 设y=（x+3）（2x+1），y=ln（2x+1），‎ 作出两个函数的图象，‎ 由图象知当x＞﹣时，两个函数没有交点，‎ 即方程f（x）=x不存在两个不同的根，‎ 即不存在满足n＞m≥0的实数m，n，当x∈[m，n]时，f（x）的值域为[m，n]．‎ ‎　‎ 请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-1：几何证明选讲]‎ ‎22．（10分）（2016•云南一模）如图，BC是⊙O的直径，EC与⊙O相切于C，AB是⊙O的弦，D是的中点，BD的延长线与CE交于E．‎ ‎（Ⅰ）求证：BC•CD=BD•CE；‎ ‎（Ⅱ）若，求AB．‎ ‎【解答】证明：（Ⅰ）∵BC是⊙O的直径，EC与⊙O相切于C，D是AC弧的中点，‎ ‎∴∠CBD=∠ECD，∠BDC=∠CDE=∠BCE=90°，‎ ‎∴△BCD∽△CED．…（3分）‎ ‎∴，‎ ‎∴BC•CD=BD•CE．…（5分）‎ 解：（Ⅱ）设BA的延长线与CD的延长线交于F，‎ ‎∵D是AC弧的中点，‎ ‎∴∠ABD=∠CBD，‎ ‎∵BC是⊙O的直径，‎ ‎∴∠BDC=∠BDF=90°，‎ ‎∴△BDC≌△BDF．‎ ‎∴CD=FD，BC=BF，‎ 在Rt△CDE中，．‎ ‎∴．‎ ‎∵∠BDC=∠BCE=90°，‎ ‎∴CD2=BD•DE，‎ ‎∴，‎ ‎∴，‎ ‎∴BF=4．…（8分）‎ 由割线定理得（FB﹣AB）•FB=FD•FC，‎ 即，解得．‎ ‎∴．…（10分）‎ ‎　‎ ‎[选修4-4：坐标系与参数方程]‎ ‎23．（2016•云南一模）在直角坐标系xOy中，直线l的参数方程为（t为参数）．在以原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ=．‎ ‎（I）直接写出直线l、曲线C的直角坐标方程；‎ ‎（II）设曲线C上的点到直线l的距离为d，求d的取值范围．‎ ‎【解答】解：（I）∵（t为参数），∴x﹣y=﹣3，即x﹣y+3=0．∴直线l的直角坐标方程是x﹣y+3=0．‎ ‎∵ρ=，∴ρ2=，即ρ2+2ρ2cos2θ=3．‎ ‎∴曲线C的直角坐标方程为3x2+y2=3，即．‎ ‎（II）曲线C的参数方程为（α为参数），‎ 则曲线C上的点到直线l的距离d==．‎ ‎∴当cos（）=1时，d取得最大值，‎ 当cos（）=﹣1时，d取得最小值．‎ ‎∴d的取值是[，]．‎ ‎　‎ ‎[选修4-5：不等式选讲]‎ ‎24．（2016•云南一模）已知f（x）=|x﹣2|+|x+1|+2|x+2|．‎ ‎（Ⅰ）求证：f（x）≥5；‎ ‎（Ⅱ）若对任意实数都成立，求实数a的取值范围．‎ ‎【解答】（Ⅰ）证明：∵，‎ ‎∴f（x）的最小值为5，∴f（x）≥5．…（5分）‎ ‎（Ⅱ）解：由（Ⅰ）知：15﹣2f（x）的最大值等于5．…（7分）‎ ‎∵，‎ ‎“=”成立，即，‎ ‎∴当时，取得最小值5．‎ 当时，，‎ 又∵对任意实数x，都成立，‎ ‎∴．∴a的取值范围为．…（10分）‎ ‎　‎ 参与本试卷答题和审题的老师有：sxs123；wkl197822；caoqz；w3239003；742048；沂蒙松；翔宇老师；minqi5；ywg2058；双曲线；zhczcb；546278733@qq.com；zlzhan；maths；gongjy；1619495736（排名不分先后）‎ 菁优网 ‎2016年8月21日