- 2021-05-13 发布 |
- 37.5 KB |
- 5页


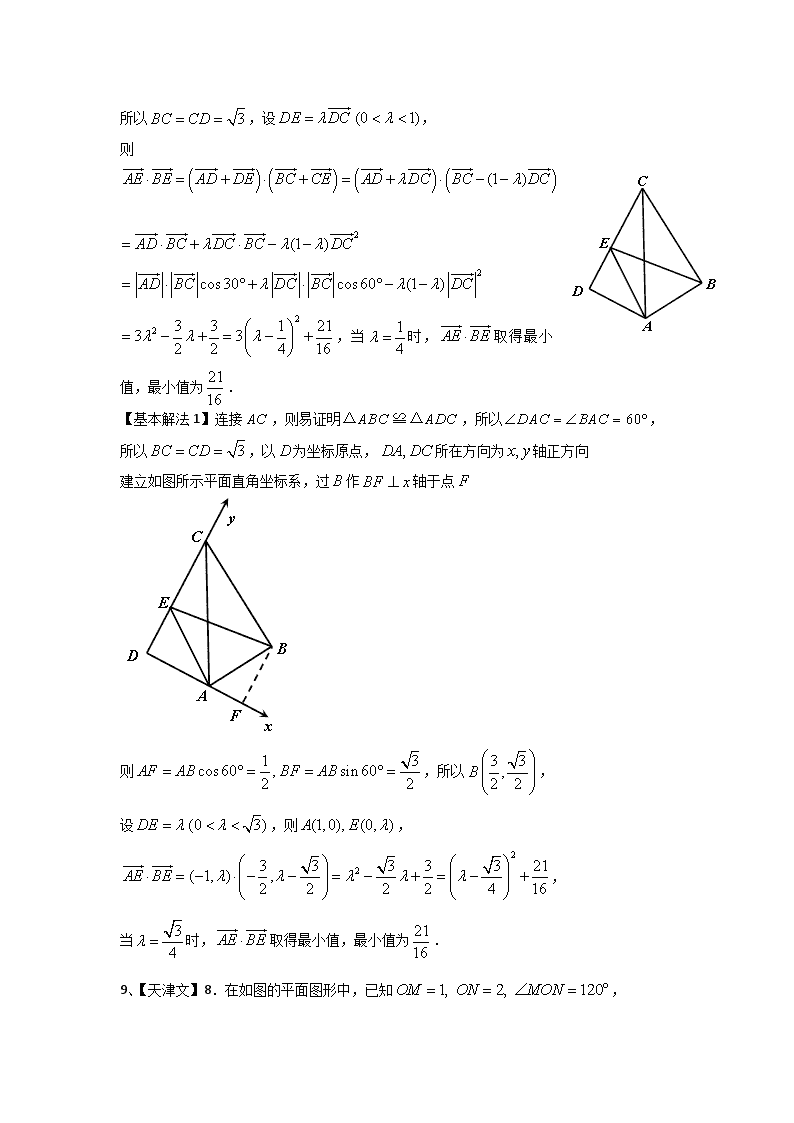
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考试题分类汇编——平面向量
2018高考分类汇编 ——平面向量 1、【北京理】6.设,均为单位向量,则“”是“”的 A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案:C; 解析:等号两边分别平方得与等价,故选C. 考点:考查平面向量的数量积性质及充分必要条件的判定; 备注:高频考点. 2、【北京文】9.设向量,若,则 ______. 答案: 【解析】因为 所以 由 得, 所以,解得 【考点】本题考查向量的坐标运算,考查向量的垂直。 3、【1卷文7理6】6.在中,为边上的中线,为的中点,则 A. B. C. D. 答案:A 解析:在中,为边上的中线,为的中点,,故选A. 4、【2卷理】4.已知向量,满足,,则 A.4 B.3 C.2 D.0 【答案】B 【解析】,故选B. 5、【2卷文】4.已知向量,满足,,则 A.4 B.3 C.2 D.0 【答案】B 解析:向量满足,则,故选B. 6、【3卷文理】13.已知向量,,,若,则 . 解析:依题意可得,又, 所以,解得. 点评:本题主要考查向量的坐标运算,以及两向量共线的坐标关系,属于基础题. 7、【上海】8.在平面直角坐标系中,已知点、,、是轴上的两个动点,且,则的最小值为 . 答案: 解析:设,则, ,最小值为. 解法2: 取中点,则.显然(当关于原点对称). 所以.则. 8、【天津理】8.如图,在平面四边形中,,,,,若点为边上的动点,则的最小值为( ) A. B. C. D.3 【答案】A 【基本解法1】连接,则易证明,所以 所以,设, 则 ,当时,取得最小值,最小值为. 【基本解法1】连接,则易证明,所以, 所以,以为坐标原点,所在方向为轴正方向 建立如图所示平面直角坐标系,过作轴于点 则,所以, 设,则, , 当时,取得最小值,最小值为. 9、【天津文】8.在如图的平面图形中,已知, ,则的值为( ) A. B. C. D.0 【答案】C 解析:, 则. 10、【浙江卷】9.已知是平面向量, 是单位向量,若非零向量与的夹角为,向量满足,则的最小值是( ) A. B. C.2 D. 【答案】A 解析:解法1:(配方法)由得,即,因此.如图,,,,则向量的终点在以为圆心,1为半径的圆上,而的终点在射线上,,问题转化为圆上的点与射线上的点连线长度最小,显然其最小值为圆心到射线的距离减去半径即为. 解法2:(向量的直径圆式)由,得,所以, 如图,,则,即终点在以为直径的圆上,以下同解法1. 解法3:(绝对值性质的应用)由,得,即, 因此,而由图形得, 所以,所以的最小值为. 解法4:(坐标法)设起点均为原点,设,,则的终点在射线上,由,得,即,所以向量的终点在圆 上,的最小值即为求圆上一点到射线上一点的最小距离, 即为.查看更多