中考数学压轴题解题策略7线段和差最值的存在性问题解题策略

中考数学压轴题解题策略7线段和差最值的存在性问题解题策略

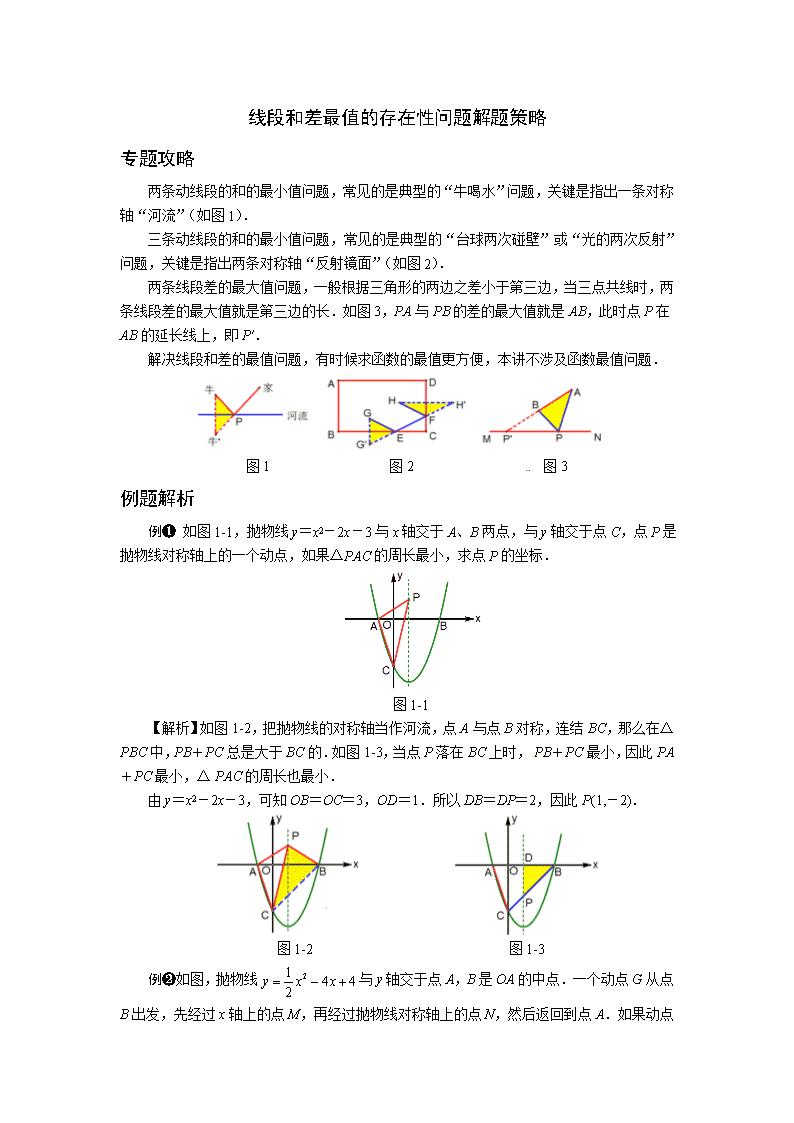
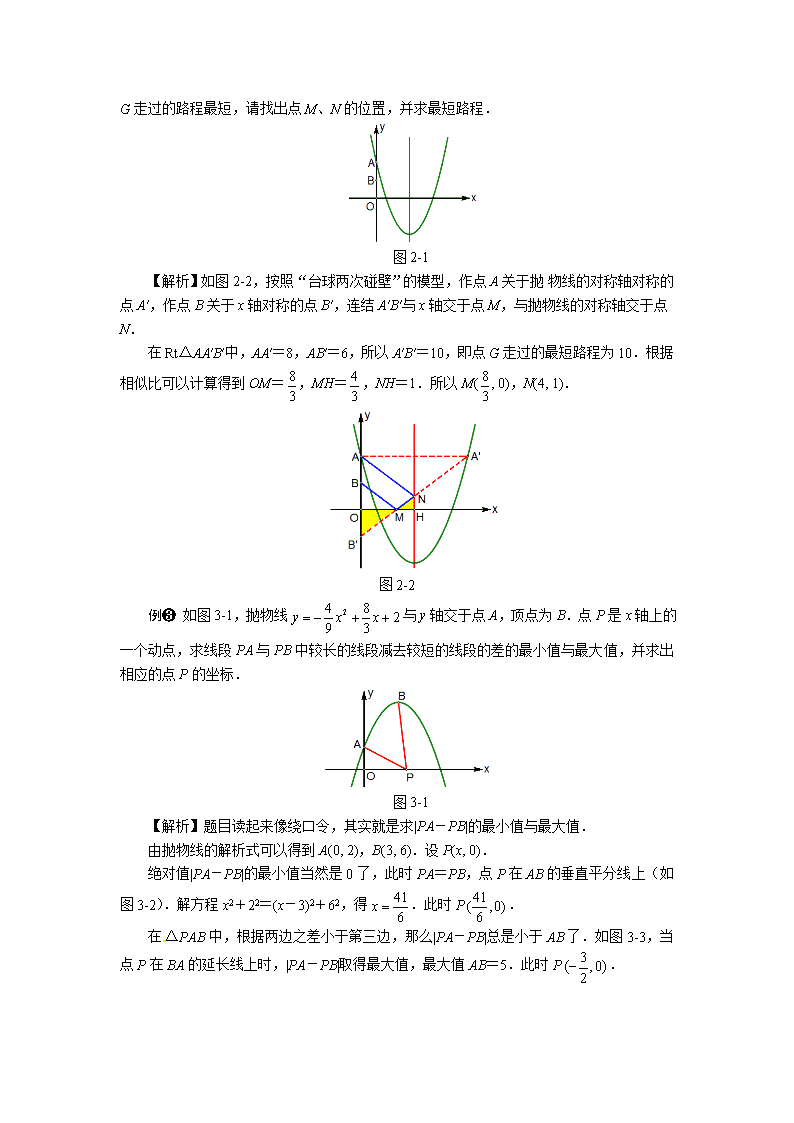
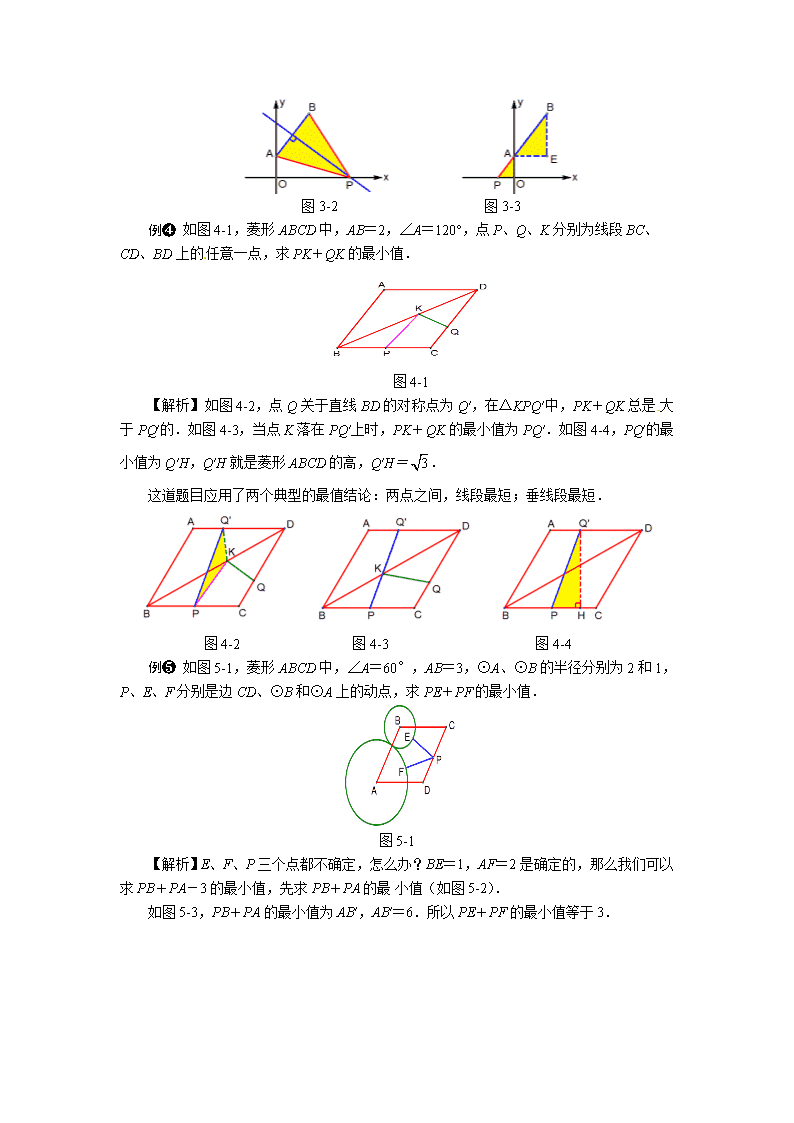
线段和差最值的存在性问题解题策略 专题攻略 两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．‎ 三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．‎ 两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．‎ 解决线段和差的最值问题，有时候求函数的最值更方便，本讲不涉及函数最值问题．‎ 图1 图2 图3‎ 例题解析 例❶ 如图1-1，抛物线y＝x2－2x－3与x轴交于A、B两点，与y轴交于点C，点P是抛物线对称轴上的一个动点，如果△PAC的周长最小，求点P的坐标．‎ 图1-1‎ ‎【解析】如图1-2，把抛物线的对称轴当作河流，点A与点B对称，连结BC，那么在△PBC中，PB＋PC总是大于BC的．如图1-3，当点P落在BC上时，PB＋PC最小，因此PA＋PC最小，△PAC的周长也最小．‎ 由y＝x2－2x－3，可知OB＝OC＝3，OD＝1．所以DB＝DP＝2，因此P(1,－2)．‎ 图1-2 图1-3‎ 例❷如图，抛物线与y轴交于点A，B是OA的中点．一个动点G从点B出发，先经过x轴上的点M，再经过抛物线对称轴上的点N，然后返回到点A．如果动点 G走过的路程最短，请找出点M、N的位置，并求最短路程．‎ 图2-1‎ ‎【解析】如图2-2，按照“台球两次碰壁”的模型，作点A关于抛物线的对称轴对称的点A′，作点B关于x轴对称的点B′，连结A′B′与x轴交于点M，与抛物线的对称轴交于点N．‎ 在Rt△AA′B′中，AA′＝8，AB′＝6，所以A′B′＝10，即点G走过的最短路程为10．根据相似比可以计算得到OM＝，MH＝，NH＝1．所以M(, 0)，N(4, 1)．‎ 图2-2‎ 例❸ 如图3-1，抛物线与y轴交于点A，顶点为B．点P是x轴上的一个动点，求线段PA与PB中较长的线段减去较短的线段的差的最小值与最大值，并求出相应的点P的坐标．‎ 图3-1‎ ‎【解析】题目读起来像绕口令，其实就是求|PA－PB|的最小值与最大值．‎ 由抛物线的解析式可以得到A(0, 2)，B(3, 6)．设P(x, 0)．‎ 绝对值|PA－PB|的最小值当然是0了，此时PA＝PB，点P在AB的垂直平分线上（如图3-2）．解方程x2＋22＝(x－3)2＋62，得．此时P．‎ 在△PAB中，根据两边之差小于第三边，那么|PA－PB|总是小于AB了．如图3-3，当点P在BA的延长线上时，|PA－PB|取得最大值，最大值AB＝5．此时P．‎ 图3-2 图3-3‎ 例❹ 如图4-1，菱形ABCD中，AB＝2，∠A＝120°，点P、Q、K分别为线段BC、CD、BD上的任意一点，求PK＋QK的最小值．‎ 图4-1‎ ‎【解析】如图4-2，点Q关于直线BD的对称点为Q′，在△KPQ′中，PK＋QK总是大于PQ′的．如图4-3，当点K落在PQ′上时，PK＋QK的最小值为PQ′．如图4-4，PQ′的最小值为Q′H，Q′H就是菱形ABCD的高，Q′H＝．‎ 这道题目应用了两个典型的最值结论：两点之间，线段最短；垂线段最短．‎ 图4-2 图4-3 图4-4‎ 例❺ 如图5-1，菱形ABCD中，∠A＝60°，AB＝3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙B和⊙A上的动点，求PE＋PF的最小值．‎ 图5-1‎ ‎【解析】E、F、P三个点都不确定，怎么办？BE＝1，AF＝2是确定的，那么我们可以求PB＋PA－3的最小值，先求PB＋PA的最小值（如图5-2）．‎ 如图5-3，PB＋PA的最小值为AB′，AB′＝6．所以PE＋PF的最小值等于3．‎ 图5-2 图5-3‎ 例❻ 如图6-1，已知A(0, 2)、B(6, 4)、E(a, 0)、F(a＋1, 0)，求a为何值时，四边形ABEF周长最小？请说明理由．‎ 图6-1‎ ‎【解析】在四边形ABEF中，AB、EF为定值，求AE＋BF的最小值，先把这两条线段经过平移，使得两条线段有公共端点．‎ 如图6-2，将线段BF向左平移两个单位，得到线段ME．‎ 如图6-3，作点A关于x轴的对称点A′，MA′与x轴的交点E，满足AE＋ME最小．‎ 由△A′OE∽△BHF，得．解方程，得．‎ 图6-2 图6-3‎ 例❼ 如图7-1，△ABC中，∠ACB＝90°，AC＝2，BC＝1．点A、C分别在x轴和y轴的正半轴上，当点A在x轴上运动时，点C也随之在y轴上运动．在整个运动过程中，求点B到原点的最大距离．‎ 图7-1‎ ‎【解析】如果把OB放在某一个三角形中，这个三角形的另外两条边的大小是确定的，那么根据两边之和大于第三边，可知第三边OB的最大值就是另两边的和．‎ 显然△OBC是不符合条件的，因为OC边的大小不确定．‎ 如图7-2，如果选AC的中点D，那么BD、OD都是定值，OD＝1，BD＝．‎ 在△OBD中，总是有OB＜OD＋BD．‎ 如图7-3，当点D落在OB上时，OB最大，最大值为．‎ 图7-2 图7-3 ‎ 例❽ 如图8-1，已知A(－2,0)、B(4, 0)、．设F为线段BD上一点（不含端点），连结AF，一动点M从点A出发，沿线段AF以每秒1个单位的速度运动到F，再沿线段FD以每秒2个单位的速度运动到D后停止．当点F的坐标是多少时，点M在整个运动过程中用时最少？‎ 图8-1‎ ‎【解析】点B(4, 0)、的坐标隐含了∠DBA＝30°，不由得让我们联想到30°角所对的直角边等于斜边的一半．‎ 如果把动点M在两条线段上的速度统一起来，问题就转化了．‎ 如图8-2，在Rt△DEF中，FD＝2FE．如果点M沿线段FD以每秒2个单位的速度运动到点D时，那么点M沿线段FE以每秒1个单位的速度正好运动到点E．因此当AF＋FE最小时，点M用时最少．‎ 如图8-3，当AE⊥DE时，AF＋FE最小，此时F．‎ 图8-2 图8-3‎ 例❾ 如图9-1，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8．点E是BC边上的点，连结AE，过点E作AE的垂线交AB边于点F，求AF的最小值．‎ 图9-1‎ ‎【解析】如图9-2，设AF的中点为D，那么DA＝DE＝DF．所以AF的最小值取决于DE的最小值．‎ 如图9-3，当DE⊥BC时，DE最小．设DA＝DE＝m，此时DB＝．‎ 由AB＝DA＋DB，得．解得．此时AF＝．‎ 图9-2 图9-3‎ 例❿ 如图10-1，已知点P是抛物线上的一个点，点D、E的坐标分别为(0, 1)、(1, 2)，连结PD、PE，求PD＋PE的最小值．‎ 图10-1‎ ‎【解析】点P不在一条笔直的河流上，没有办法套用“牛喝水”的模型．‎ 设P，那么PD2＝．所以PD＝．‎ 如图10-2，的几何意义可以理解为抛物线上的动点P到直线y＝－1的距离PH．所以PD＝PH．因此PD＋PE就转化为PH＋PE．‎ 如图10-3，当P、E、H三点共线，即PH⊥x轴时，PH＋PE的最小值为3．‎ 高中数学会学到，抛物线是到定点的距离等于到定直线的距离的点的集合，在中考数学压轴题里, 如果要用到这个性质，最好铺垫一个小题，求证PD＝PH. ‎ 图10-2 图10-3‎